并查集-(union-find sets)

在某些应用，要将n个不同元素分成一组不相交的集合，并且在各些集合上要提供两个操作，一个实查找一个元素所属的集合另一个操作是合并两个集合。应用有求一个图的连通分量个数。还有Kruscal算法中判断是否出现环。 其实并查集数据结构非常简单， 下面介绍的版本考虑了优化。 因为可能出现如下图所示的情况：

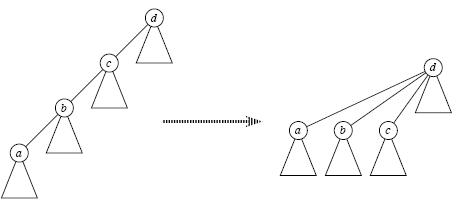
在这做图的情况下查找一个点所属的集合的时间复杂度是O(n)，就失去并查集说具有的高效性。因此在查找的时候递归找到祖先节点，在回溯的时候将子孙节点直接指向祖先节点，如右图所示。下面给出并查集算法的三个核心函数：

 1int father[MAX];   /* father[x]表示x的父节点*/
 2int rank[MAX];     /* rank[x]表示x的秩*/
 3
 4
 5/* 初始化集合*/
 6void Init(int x)
 7{
 8    father[x] = x; //根据实际情况指定的父节点可变化
 9    rank[x] = 0;   //根据实际情况初始化秩也有所变化
10}
11
12
13/* 查找x元素所在的集合,回溯时压缩路径*/
14int Find(int x)
15{
16    if (x != father[x])
17    {
18        father[x] = Find(father[x]); //这个回溯时的压缩路径是精华
19    }
20    return father[x];
21}
22
23
24/* 
25   按秩合并x,y所在的集合
26   下面的那个if else结构不是绝对的，具体根据情况变化
27   但是，宗旨是不变的即，按秩合并，实时更新秩。
28*/
29void Union(int x, int y)
30{
31    x = Find(x);
32    y = Find(y);
33    if (x == y) return;
34    if (rank[x] > rank[y]) 
35    {
36        father[y] = x;
37    }
38    else
39    {
40        if (rank[x] == rank[y])
41        {
42            rank[y]++;
43        }
44        father[x] = y;
45    }
46}