第二集 矩阵消元
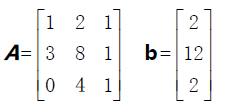
高斯消元法通过对方程组中的某两个方程进行适当的数乘和加和,以达到将某一未知数系数变为零,从而削减未知数个数的目的。解线性方程组的基本思路是把方程组通过行初等变换用一个很简单的等价方程组(即相同解集)代替。


矩阵A 为可逆矩阵,消元结束后得到上三角阵U,其左侧下半部分的元素均为0,而主元1,2,5 分列在U 的对角线上。 主元之积即行列式的值。
需要说明的是, 主元不能为0,如果恰好消元至某行,0 出现在了主元的位置上,应当通过与下方一行进行“ 行交换”使得非零数字出现在主元位置上。如果0 出现在了主元位置上,并且下方没有对等位置为非0 数字的行,则 消元失效, 说明矩阵A 为不可逆矩阵,且线性方程组没有唯一解(可能无解,可能无穷多解)。

回代是应用增广矩阵,将b 插入矩阵A之后形成最后一列,在消元过程中带着b 一起操作(Matlab 是算完系数矩阵再处理b 的)。
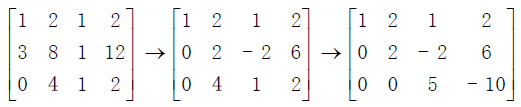
此时我们将原方程 Ax=b 转化为了新的方程 Ux=c ,其中c=《[2;6;-10]》。从最后一行得到z=-2,依次回代可以得到y=1和x=2。
消元矩阵
矩阵运算的核心内容就是对“ 行”或者“ 列”进行独立操作。
矩阵右乘列向量
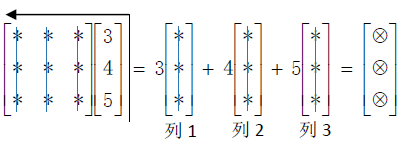
矩阵左乘行向量
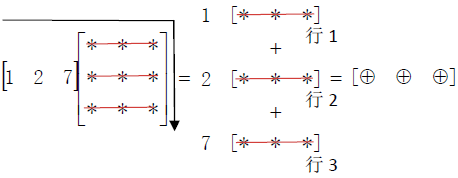
左乘的这个矩阵为“初等矩阵”(Elementary Matrix),因此记做E。
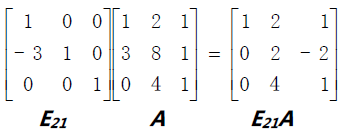
按行运算
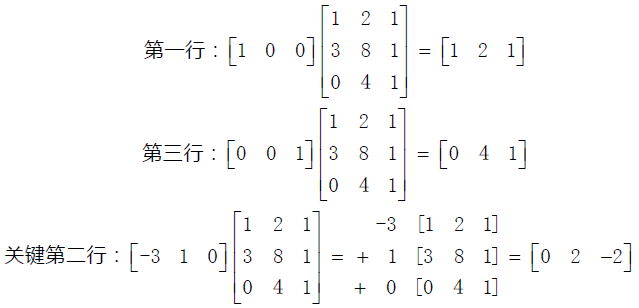
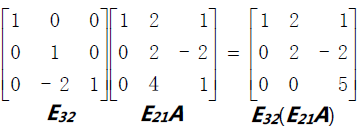
3*3 矩阵的消元本来应该分三步完成,最终得到 E32(E31(E21A)) 。本例中 E31=I ,
所以结果变为 E32(E21A)=U ,因为矩阵运算符合结合律,也可写作 (E32E21)A=U 。
可以记作 EA=U 。
方程 Ax=b 的解也满足方程 Ux=EAx=Eb=c ,因此我们将问题转化为 Ux=c 。回代可以表示为 E[A|b]=[U|c] 。
第三集 矩阵的乘法和逆矩阵
矩阵乘法
矩阵A 与B 相乘得到矩阵C。其中A 为m*n(m行n 列)矩阵,而B 为n*p 矩阵,则C 为m*p 矩阵,记
cij
为矩阵C 中第i 行第j列的元素。
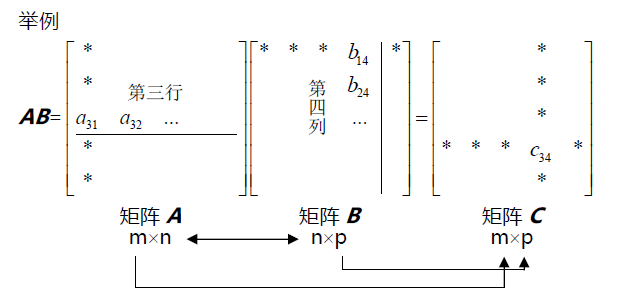
1)标准方法(行乘以列)
本质上矩阵的代数运算就是线性方程组的运算
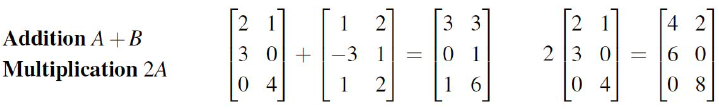
比如有矩阵形式y=Ax,A 为m*n 矩阵;z=Bx,B 为m*n 矩阵。
y+z=(A+B)x, 所以矩阵加法运算规则就只能形状相同的矩阵进行加和。αy=αAx,数乘要在矩阵每个元素上乘以α。
而矩阵乘法可以视为给线性方程组做变量替换

2)列操作
矩阵C的第j列是通过矩阵A乘以矩阵B 第j列的列向量得到的。
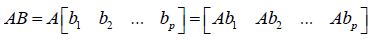
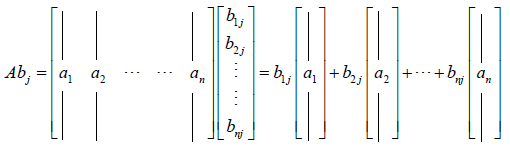
3)行操作
矩阵C 的第i行是通过矩阵A 的第i行乘以矩阵B得到的。
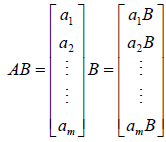
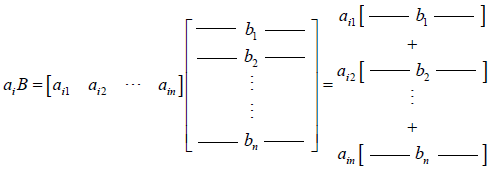
4)列乘以行
矩阵A 的第k 列是一个m*1 的向量,而矩阵B 第k 行是一个1*p 的向量,两向量相乘会得到一个矩阵
Ck
,将所有的n 个矩阵相加记得到C。
Ck
的所有行向量共线,行空间是
[bk1…bkp]
上的直线,
[a1k...amk]
的各个分量是系数;所有的列向量共线,列空间是
[a1k...amk]
上的直线,
[bk1...bkp]
的各个分量是系数。
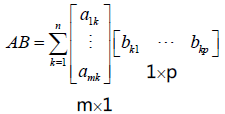
分块乘法(略,见笔记)
逆矩阵
消元矩阵之逆矩阵的实施效果就是抵消原矩阵的消元操作。消元矩阵实现了对原矩阵A 的操作,使第二行行向量[3,8,1]减掉了第一行[1,2,1]的3 倍变为[0,2,-2],则逆向操作就应该是把现在的第二行行向量[0,2,-2]加上第一行[1,2,1]的3 倍,从而变回原来的第二行[3,8,1]。

如果矩阵A 是方阵,若存在逆矩阵
A−1
,使得
A−1A=I=AA−1
(左逆矩阵等于右逆矩阵)。我们称矩阵A 可逆或者矩阵A 非奇异。反之,如果A 为奇异,则其没有逆矩阵。它的行列式为0。
例如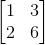
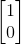
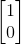
若矩阵A 存在逆矩阵,则方程Ax=0 只有零解。证明:反设其存在
非零解x,则有
x=(A−1A)x=A−1(Ax)=A−10=0
,矛盾。
高斯-若尔当消元法
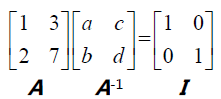
求逆相当于两组方程:
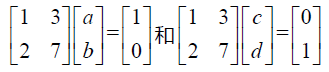
高斯-若尔当消元法可以同时处理两个方程:
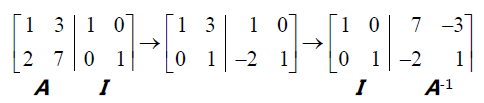
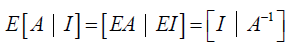
第四集 矩阵的LU 分解
在没有行交换的情况下,矩阵A 通过左乘一系列消元矩阵
Eij
可以转化为U。在二阶矩阵中,进行一次消元操作即可达到这一效果。
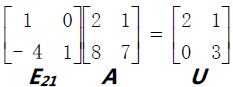
在等式两侧左乘,得到
E−121E21A=E−121U即A=E−121U
。就得到了矩阵A 的LU分解结果。
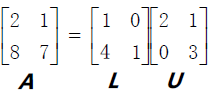
其中U 为上三角阵(Upper triangular matrix),主元依次排列于它的对角线上,E21‐1 即L 为下三角阵(Lower triangular matrix)。有时我们也通过分解得到对角阵D(diagonal matrix),例如
对于三阶矩阵不需要换行进行消元的情况则有:
E32(E31(E21A))=U
,左乘逆矩阵可得
A=E−121E−131E−132U=LU
设定一组消元矩阵,其中
E31
为单位阵I,其它两个消元矩阵如下:
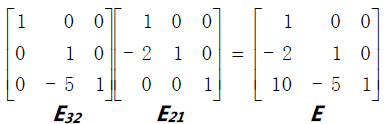
可以看到在消元矩阵E 的左下角出现了数10。它的出现是由于第一步操作E21中“第二行”减去了2 倍的“第一行”得到了“新第二行”。而在第二步操作E32 中第三行减去了5 倍的“新第二行”。row3-5newrow2=row3-5(row2-2row1)=row3-5row2+10row1。运算顺序是从第一行第一个元素往下计算,运算第三行时可能第二行已改变。
在右侧操作则不会有这种情况发生,运算顺序会发生变化,
L=E−1=E−121E−132
。运算顺序是从倒数第一行最后一个元素往上计算,运算第三行时第二行不可能改变。
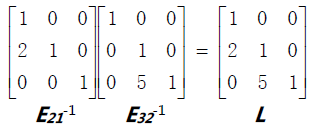
如果没有行交换操作,则消元矩阵的因子可以直接写入矩阵L。没有多余的交叉项出现是LU 分解要优于EA=U 这种形式的原因之一。
消元法所需运算量(略,见笔记)
行交换
如果主元的位置出现了0,就需要进行“行交换”。我们可以通过左乘一个置换矩阵实现“行交换”的操作。所有的3*3 的置换矩阵包括:
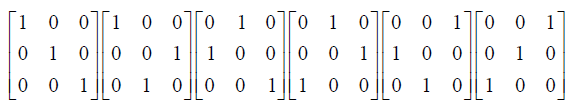
置换矩阵是进行了行交换的单位矩阵。对于n*n矩阵存在着n!个置换矩阵。
对于某阶的置换矩阵集合而言,置换矩阵的两两乘积(相当于进行两次行交换操作)仍在这个集合中(因为对一个矩阵所有的行交换操作都在这个集合中),置换矩阵的逆矩阵也在此集合中(一次行交换的逆操作也是一次行变换)。
置换矩阵的逆矩阵即为它的转置
P−1=PT
。
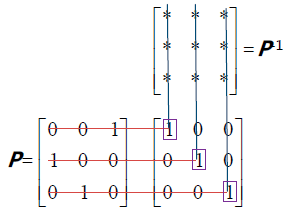
P 的第i 行和
P−1
的第i 列相乘会得到1,与其他列相乘都得到0,所以
P−1
第i列只能是P 的第i 行行向量的转置(让分量1 出现在向量里的相同位置)。
A=LU
是假设没有进行行交换的情况,如果需要换行进行消元的情况则是
PA=LU
。可以假想在消元过程中你已经完全知道需要怎么进行“行交换”之后,我们重新开始做矩阵分解,这一次先对
A
进行“行交换”得到
A∗
,这时候对
A∗
消元,就不用再进行“行交换”了,于是有
PA=A∗=LU
。
转置
矩阵
A
的转置矩阵记为
若
A
是对称矩阵则有
给定一个矩阵
参考文献:
线性代数及其应用(美)David C.LayPDF
豆丁网MIT-线性代数笔记(上)








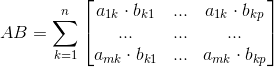
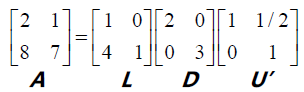














 2055
2055

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








