第十周 项目3 - 二叉树的构造

1.由先序序列和中序序列构造二叉树

• 定理：任何n（n≥0）个不同节点的二叉树，都可由它的中序序列和先序序列唯一地确定。
• 证明（数学归纳法） 
  基础：当n=0时，二叉树为空，结论正确。 
  假设：设节点数小于n的任何二叉树，都可以由其先序序列和中序序列唯一地确定。 
  归纳：已知某棵二叉树具有n（n＞0）个不同节点，其先序序列是 a0a1…an−1 ；中序序列是 b0b1…bk−1bkbk+1…bn−1 。 
  
  • 先序遍历“根-左-右”， a0 必定是二叉树的根节点
  • a0 必然在中序序列中出现，设在中序序列中必有某个 bk（0≤k≤n−1） 就是根节点 a0 。 
    
  • 由于 bk 是根节点，中序遍历“左-根-右”，故中序序列中 b0b1…bk−1 必是根节点 bk(a0) 左子树的中序序列，即 bk 的左子树有k个节点， bk+1…bn−1 必是根节点 bk（a0） 右子树的中序序列，即 bk 的右子树有 n−k−1 个节点。
  • 对应先序序列，紧跟在根节点 a0 之后的k个节点 a1…ak 是左子树的先序序列， ak+1…an−1 这 n−k−1 就是右子树的先序序列。 
    
  • 根据归纳假设，子先序序列 a1…ak 和子中序序列 b0b1…bk−1 可以唯一地确定根节点 a0 的左子树，而先序序列 ak+1…an−1 和子中序序列 bk+1…bn−1 可以唯一地确定根节点 a0 的右子树。
  • 综上所述，这棵二叉树的根节点己经确定，而且其左、右子树都唯一地确定了，所以整个二叉树也就唯一地确定了。

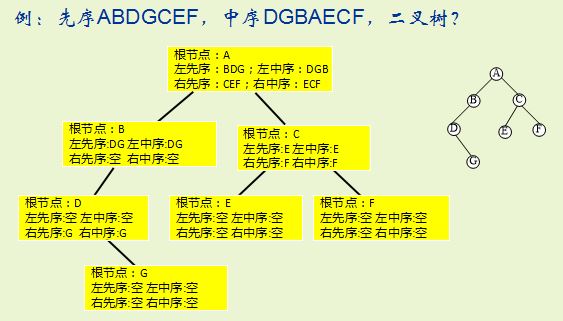
• 例 
  

  根据定理的证明，写出下面的算法。

  品味：以上构造性证明是突出体现计算机科学的案例。计算机学科的精髓就在于制造，即使在“理论性”味道的定理中，其证明过程，给出的就是“存在的这么一个东西”的构造方法。

［参考解答］（btreee.h见算法库）

#include <stdio.h>
#include <malloc.h>
#include "btree.h"

BTNode *CreateBT1(char *pre,char *in,int n)
/*pre存放先序序列,in存放中序序列,n为二叉树结点个数,
本算法执行后返回构造的二叉链的根结点指针*/
{
    BTNode *s;
    char *p;
    int k;
    if (n<=0) return NULL;
    s=(BTNode *)malloc(sizeof(BTNode));     //创建二叉树结点*s
    s->data=*pre;
    for (p=in; p<in+n; p++)                 //在中序序列中找等于*ppos的位置k
        if (*p==*pre)                       //pre指向根结点
            break;                          //在in中找到后退出循环
    k=p-in;                                 //确定根结点在in中的位置
    s->lchild=CreateBT1(pre+1,in,k);        //递归构造左子树
    s->rchild=CreateBT1(pre+k+1,p+1,n-k-1); //递归构造右子树
    return s;
}

int main()
{
    ElemType pre[]="ABDGCEF",in[]="DGBAECF";
    BTNode *b1;
    b1=CreateBT1(pre,in,7);
    printf("b1:");
    DispBTNode(b1);
    printf("\n");
    return 0;
}
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

2.由后序序列和中序序列构造二叉树

• 定理：任何n（n＞0）个不同节点的二叉树，都可由它的中序序列和后序序列唯一地确定。
• 证明：(略) 
  

［参考解答］（btreee.h见算法库）

#include <stdio.h>
#include <malloc.h>
#include "btree.h"

BTNode *CreateBT2(char *post,char *in,int n)
/*post存放后序序列,in存放中序序列,n为二叉树结点个数,
本算法执行后返回构造的二叉链的根结点指针*/
{
    BTNode *s;
    char r,*p;
    int k;
    if (n<=0) return NULL;
    r=*(post+n-1);                          //根结点值
    s=(BTNode *)malloc(sizeof(BTNode));     //创建二叉树结点*s
    s->data=r;
    for (p=in; p<in+n; p++)                 //在in中查找根结点
        if (*p==r)
            break;
    k=p-in;                                 //k为根结点在in中的下标
    s->lchild=CreateBT2(post,in,k);         //递归构造左子树
    s->rchild=CreateBT2(post+k,p+1,n-k-1);  //递归构造右子树
    return s;
}

int main()
{
    ElemType in[]="DGBAECF",post[]="GDBEFCA";
    BTNode *b2;
    b2=CreateBT2(post,in,7);
    printf("b2:");
    DispBTNode(b2);
    printf("\n");
    return 0;
}
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

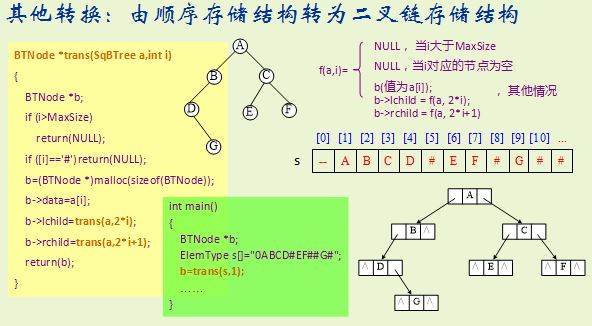
3.由顺序存储结构转为二叉链存储结构 

［参考解答］（btreee.h见算法库）

#include <stdio.h>
#include <malloc.h>
#include "btree.h"
#define N 30
typedef ElemType SqBTree[N];
BTNode *trans(SqBTree a,int i)
{
    BTNode *b;
    if (i>N)
        return(NULL);
    if (a[i]=='#')
        return(NULL);           //当节点不存在时返回NULL
    b=(BTNode *)malloc(sizeof(BTNode)); //创建根节点
    b->data=a[i];
    b->lchild=trans(a,2*i);                 //递归创建左子树
    b->rchild=trans(a,2*i+1);               //递归创建右子树
    return(b);                              //返回根节点
}
int main()
{
    BTNode *b;
    ElemType s[]="0ABCD#EF#G####################";
    b=trans(s,1);
    printf("b:");
    DispBTNode(b);
    printf("\n");
    return 0;
}