笔试练习day6

NC1 大数加法

大数加法_牛客题霸_牛客网 (nowcoder.com)

描述

以字符串的形式读入两个数字，编写一个函数计算它们的和，以字符串形式返回。

数据范围：𝑠.𝑙𝑒𝑛𝑔𝑡ℎ,𝑡.𝑙𝑒𝑛𝑔𝑡ℎ≤100000s.lengt**h,t.lengt**h≤100000，字符串仅由’0’~‘9’构成

要求：时间复杂度 𝑂(𝑛)O(n)

示例1

输入：

"1","99"

返回值：

"100"

说明：

1+99=100       

示例2

输入：

"114514",""

返回值：

"114514"

代码

#include <algorithm>
class Solution {
public:

    string add(string a,string b)
    {
        reverse(a.begin(),a.end());
        reverse(b.begin(),b.end());
        int k=0;
        string ret;
        int left=0;
        int right=0;

        while(left<a.size()||right<b.size())
        {

            if(left<a.size())k+=a[left++]-'0';
            if(right<b.size())k+=b[right++]-'0';

            ret+=k%10+'0';
            k=k/10;
        }
        if(k>0) ret+=k+'0';
        reverse(ret.begin(),ret.end());
        return ret;
    }
    string solve(string s, string t) {
        return add(s,t);
    }
};

NC40 链表相加(二)

链表相加(二)_牛客题霸_牛客网 (nowcoder.com)

描述

假设链表中每一个节点的值都在 0 - 9 之间，那么链表整体就可以代表一个整数。

给定两个这种链表，请生成代表两个整数相加值的结果链表。

数据范围：0≤𝑛,𝑚≤10000000≤n,m≤1000000，链表任意值 0≤𝑣𝑎𝑙≤90≤val≤9
要求：空间复杂度 𝑂(𝑛)O(n)，时间复杂度 𝑂(𝑛)O(n)

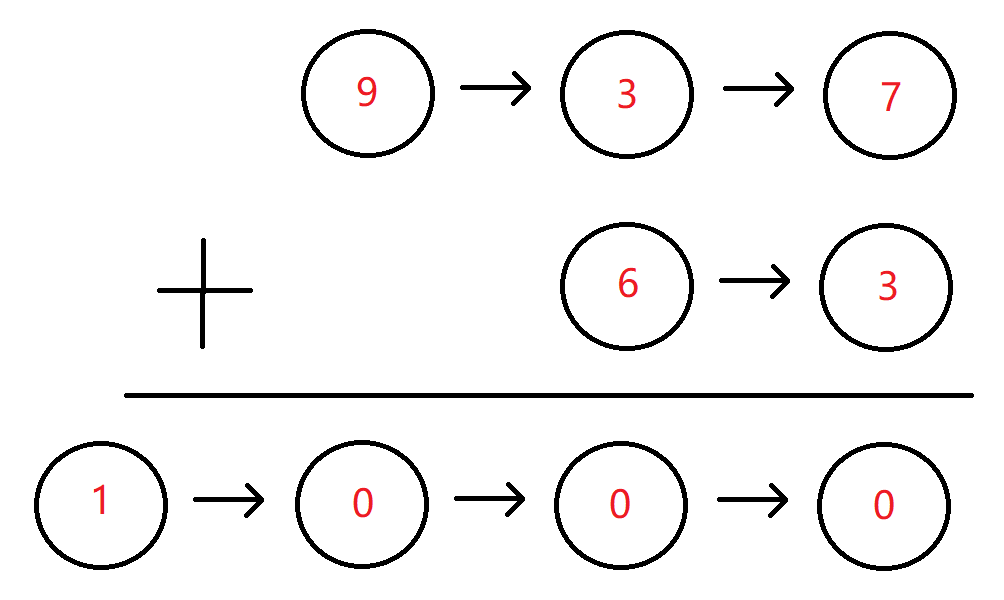
例如：链表 1 为 9->3->7，链表 2 为 6->3，最后生成新的结果链表为 1->0->0->0。

示例1

输入：

[9,3,7],[6,3]

复制

返回值：

{1,0,0,0}

复制

说明：

如题面解释     

示例2

输入：

[0],[6,3]

复制

返回值：

{6,3}

复制

备注：

1≤𝑛,𝑚≤1061≤n,m≤106
0≤𝑎𝑖,𝑏𝑖≤90≤ai,bi≤9

代码

class Solution {
public:
    /**
     * 
     * @param head1 ListNode类 
     * @param head2 ListNode类 
     * @return ListNode类
     */
    ListNode* reverse(ListNode* head) {
        if(head==nullptr || head->next==nullptr)
            return head;
        ListNode *a=nullptr, *b=head, *c=head->next;
        while(c!=nullptr) {
            b->next=a;
            a=b;
            b=c;
            c=c->next;
        }
        b->next=a;
        return b;
    }
    ListNode* addInList(ListNode* head1, ListNode* head2) {
        ListNode* A=reverse(head1); //反转链表
        ListNode* B=reverse(head2); //反转链表
        ListNode* a=A, *b=B;
        int sum=0;
        ListNode* res=new ListNode(0);
        ListNode* cur=res;
        while(a!=nullptr || b!=nullptr || sum>0) {
            if(a!=nullptr) {
                sum+=a->val;
                a=a->next;
            }
            if(b!=nullptr) {
                sum+=b->val;
                b=b->next;
            }
            cur->next=new ListNode(sum%10);
            sum/=10;
            cur=cur->next;
        }
        cur=reverse(res->next);
        //释放额外空间
        delete res;
        //复原现场
        head1=reverse(head1);
        head2=reverse(head2);
        return cur;
    }
};

大数乘法

大数乘法__牛客网 (nowcoder.com)

class Solution {   
public:   
    string solve(string s, string t) {   
        reverse(s.begin(),s.end());   
        reverse(t.begin(),t.end());   
		//无进位相乘   
        vector<int> tmp(s.size()+t.size());   
        for(int i =0;i < s.size();i++)   
        {
            for(int j=0;j<t.size();j++)   
            {
                tmp[i+j] += (s[i]-'0')*(t[j]-'0');    
            }
        }
		//相加处理进位   
        int k=0;   
        string ret;   
        for(auto e:tmp)   
        {
            e+=k;
            ret+=e%10+'0';
            k=e/10;
        }
        while(k)
        {
            ret+=k%10+'0';
            k/=10;
        }
		//处理前导0
        while(ret.size()!=1&&ret.back()=='0')
        {
            ret.pop_back();
        }
        reverse(ret.begin(),ret.end());
        return ret;
    }
};

    {
            ret+=k%10+'0';
            k/=10;
        }
		//处理前导0
        while(ret.size()!=1&&ret.back()=='0')
        {
            ret.pop_back();
        }
        reverse(ret.begin(),ret.end());
        return ret;
    }
};