单源最短路径:SPFA算法
概述
SPFA(Shortest Path Faster Algorithm)算法,是西南交通大学段凡丁于 1994 年发表的,其在Bellman-ford算法的基础上加上一个队列优化,减少了冗余的松弛操作,是一种高效的最短路算法。
问题
在带权有向图G=(V,A)中,假设每条弧A[i]的长度为w[i],找到由顶点V0到其余各点的最短路径。
算法描述
算法思想
设立一个队列用来保存待优化的顶点,优化时每次取出队首顶点u,并且用u点当前的最短路径估计值dist[u]对与u点邻接的顶点v进行松弛操作,如果v点的最短路径估计值dist[v]可以更小,且v点不在当前的队列中,就将v点放入队尾。这样不断从队列中取出顶点来进行松弛操作,直至队列空为止。
判断有无负环:如果某个点进入队列的次数大于等于总节点数则存在负环(SPFA无法处理带负环的图)。
算法过程

首先建立源点到各点的最短距离表格

首先源点入队,当队列非空时:
1. 队首节点a出队,对a的所有出边邻接点进行松弛操作(此处有b,c,d三个点),此时距离表格状态为:

在松弛时源点到这三个点的距离都变小了,且这些点现在都不在队列内,于是将这些点入队。
2. 队首节点b点出队,对b的所有出边邻接点进行松弛操作(此处只有e点),此时距离表格状态为:

e的距离估值也变小了,且e不在队内,于是将e入队。此时队列中的节点为c,d,e。
3. 队首节点c出队,对c的所有出边邻接点进行松弛操作(此处有e,f两个点),此时距离表格状态为:

e,f的距离估值都变小了,但e已经在队列中,所以只有f需要入队。此时队列中的节点为d,e,f。
4. 依此类推,之后的距离表格状态依次为:





(为什么最后出现了两张一模一样的图?因为倒数第二个在队列内的节点e对唯一一个出边邻接点g松弛不成功,g的距离估值没有变化;最后一个在队列内的节点b对唯一一个出边邻接点e松弛不成功,e的距离估值也没有变化)
到这里,队列为空,算法执行完成。
程序代码
SPFA的两种写法,bfs和dfs,bfs判别负环不稳定,相当于限深度搜索,但是设置得好的话还是没问题的,dfs的话判断负环很快。
/*
FILE:spfa_bfs.cpp
LANG:C++
*/
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int node_num = 100; //最大节点数
const int INF = 2147483647;
int matrix[node_num][node_num]; //邻接矩阵
int dist[node_num]; //距离估值
int path[node_num]; //记录前驱节点
bool vis[node_num]; //记录节点是否在队列内
int v_num, a_num; //记录节点数、弧数
bool spfa_bfs(const int);
int main()
{
cout << "v_num:";
cin >> v_num;
cout << "a_num:";
cin >> a_num;
for (int i = 0; i < v_num; ++i)
{
for (int j = 0; j < v_num; ++j)
{
matrix[i][j] = ((i != j) ? INF : 0); //初始化邻接矩阵
}
}
int u, v, w;
for (int i = 0; i < a_num; ++i)
{
cin >> u >> v >> w;
matrix[u][v] = matrix[v][u] = w;
}
int src;
cout << "source:";
cin >> src;
if (spfa_bfs(src))
{
cout << "E" << endl; //存在负环
return 0;
}
for (int i = 0; i < v_num; ++i)
{
if (i == src)
{
continue;
}
cout << src << "->" << i << ":" << dist[i] << ":" << i;
int t = path[i];
while (t != src)
{
cout << "-" << t;
t = path[t];
}
cout << "-" << src << endl; //倒序输出最短路径
}
return 0;
}
bool spfa_bfs(const int src)
{
memset(vis, false, sizeof(vis));
queue<int> q;
int cnt[node_num] = {0}; //记录每个节点的进队次数
for (int i = 0; i < v_num; ++i)
{
dist[i] = INF; //初始化距离表
path[i] = src; //初始化前驱节点表
}
dist[src] = 0; //设置源点距离自己的距离为0
q.push(src); //源点进队
vis[src] = true; //打上进队标记
++cnt[src]; //记录进队次数
while (!q.empty()) //队列非空则一直循环
{
int x;
x = q.front(); //读取队首节点
q.pop(); //弹出队首节点
vis[x] = false; //去除队列标记
for (int i = 0; i < v_num; ++i)
{
if (matrix[x][i] != INF && dist[x] + matrix[x][i] < dist[i]) //如果i是读取的节点的出边邻接点且可以进行松弛操作
{
dist[i] = dist[x] + matrix[x][i]; //松弛操作
path[i] = x; //更新前驱
if (!vis[i]) //如果不在队列内
{
q.push(i); //进队
vis[i] = true; //打上标记
++cnt[i]; //记录进队次数
if (cnt[i] >= v_num) //如果这个节点的进队次数大于等于节点总数
{
return true; //说明存在负环,无法处理
}
}
}
}
}
return false;
}/*
FILE:spfa_dfs.cpp
LANG:C++
*/
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int node_num = 100;
const int INF = 2147483647;
int matrix[node_num][node_num], dist[node_num], path[node_num];
bool vis[node_num];
int v_num, a_num;
queue<int> q;
bool spfa_dfs(const int);
int main()
{
cout << "v_num:";
cin >> v_num;
cout << "a_num:";
cin >> a_num;
for (int i = 0; i < v_num; ++i)
{
for (int j = 0; j < v_num; ++j)
{
matrix[i][j] = ((i != j) ? INF : 0);
}
}
int u, v, w;
for (int i = 0; i < a_num; ++i)
{
cin >> u >> v >> w;
matrix[u][v] = matrix[v][u] = w;
}
int src;
cout << "source:";
cin >> src;
memset(vis, false, sizeof(vis));
for (int i = 0; i < v_num; ++i)
{
dist[i] = INF;
path[i] = src;
}
dist[src] = 0;
if (spfa_dfs(src))
{
cout << "E" << endl;
return 0;
}
for (int i = 0; i < v_num; ++i)
{
if (i == src)
{
continue;
}
cout << src << "->" << i << ":" << dist[i] << ":" << i;
int t = path[i];
while (t != src)
{
cout << "-" << t;
t = path[t];
}
cout << "-" << src << endl;
}
return 0;
}
bool spfa_dfs(const int src)
{
q.push(src);
vis[src] = true;
while (!q.empty())
{
int x;
x = q.front();
q.pop();
vis[x] = false;
for (int i = 0; i < v_num; ++i)
{
if (matrix[x][i] != INF && dist[x] + matrix[x][i] < dist[i])
{
dist[i] = dist[x] + matrix[x][i];
path[i] = x;
if (!vis[i])
{
if (spfa_dfs(i))
{
return true;
}
}
}
}
}
return false;
}示例图:

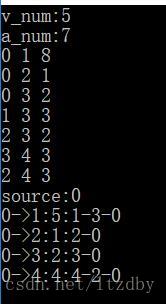
运行结果:
算法优化
SPFA算法有两个优化算法SLF和LLL:
SLF:Small Label First策略,设要加入的节点是j,队首元素为i,若dist(j)<dist(i),则将j插入队首,否则插入队尾。
LLL:Large Label Last策略,设队首元素为i,每次弹出时进行判断,队列中所有dist值的平均值为x,若dist(i)>x则将i插入到队尾,查找下一元素,直到找到某一i使得dist(i)<=x,则将i出对进行松弛操作。
代码:
/*
FILE:spfa_bfs_slf_lll.cpp
LANG:C++
*/
#include <iostream>
#include <cstring>
#include <deque>
using namespace std;
const int node_num = 100;
const int INF = 2147483647;
int matrix[node_num][node_num], dist[node_num], path[node_num];
bool vis[node_num];
int v_num, a_num, sum = 0, num = 1; //sum记录队列中所有节点的dist之和,num记录队列中节点数
bool spfa_bfs_slf_lll(const int);
int main()
{
cout << "v_num:";
cin >> v_num;
cout << "a_num:";
cin >> a_num;
for (int i = 0; i < v_num; ++i)
{
for (int j = 0; j < v_num; ++j)
{
matrix[i][j] = ((i != j) ? INF : 0);
}
}
int u, v, w;
for (int i = 0; i < a_num; ++i)
{
cin >> u >> v >> w;
matrix[u][v] = matrix[v][u] = w;
}
int src;
cout << "source:";
cin >> src;
if (spfa_bfs_slf_lll(src))
{
cout << "E" << endl;
return 0;
}
for (int i = 0; i < v_num; ++i)
{
if (i == src)
{
continue;
}
cout << src << "->" << i << ":" << dist[i] << ":" << i;
int t = path[i];
while (t != src)
{
cout << "-" << t;
t = path[t];
}
cout << "-" << src << endl;
}
return 0;
}
bool spfa_bfs_slf_lll(const int src)
{
memset(vis, false, sizeof(vis));
deque<int> q;
int cnt[node_num] = {0};
for (int i = 0; i < v_num; ++i)
{
dist[i] = INF;
path[i] = src;
}
dist[src] = 0;
q.push_back(src);
vis[src] = true;
++cnt[src];
while (!q.empty())
{
int x = q.front();
q.pop_front();
if (dist[x] * num > sum) //LLL策略
{
q.push_back(x);
continue;
}
vis[x] = false;
sum -= dist[x];
--num;
for (int i = 0; i < v_num; ++i)
{
if (matrix[x][i] != INF && dist[x] + matrix[x][i] < dist[i])
{
dist[i] = dist[x] + matrix[x][i];
path[i] = x;
if (!vis[i])
{
vis[i] = true;
if (dist[i] < dist[q.front()]) //SLF策略
{
q.push_front(i);
}
else
{
q.push_back(i);
}
sum += dist[i];
++num;
++cnt[i];
if (cnt[i] >= v_num)
{
return true;
}
}
}
}
}
return false;
}























 670
670

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








