最近闲的无聊,算法一直是弱项,正好hihocoder上面开始了每周的比赛,
这周的题目是01背包问题。正好归纳和总结一下。
所有的动态规划问题都两个特点:
1、重复子问题:一个问题可以转化成几个同类型的子问题。
2、后无关性:前一个问题产生的决策和结果,对下一个问题没有影响。
说白了,就是你能吧问题写成简单的数学递归表达式:
对于01背包问题,建模很关键,
这里面有几个关键量
物品个数N
能容纳的重量M
每个物品的价值V(i)
每个物品的重量w(i)
我们要想好这个数学表达式
对于每个物品而言,有两种状态,被选上和不被选上, 即0和1状态。而对整个背包而言 能够承受的重量就是里面物品的加和,同样价值一样也是加和。
我们希望背包尽可能装得多,而且产生的价值最大,(最重要的的是总价值最高)
所以整个表达式应该以价值作为衡量因素。
下面是表达式:
N个物品,背包有M重量空余,等于在前N-1选择最大的,一种是不选择第N-1个物品,另一种是选择第N-1个物品,并占据了背包Wn的重量,但提供了Vn的价值。
下面是三种代码形式,孰优孰劣,大家一眼就能开出来。
public int getcurrentVlue(int i,int j){
if(i==0){
if(j>=0) return 0;
}
if(j<0) return Integer.MIN_VALUE;
return max (getcurrentVlue(i-1, j),getcurrentVlue(i-1, j-w[i-1])+v[i-1]);
} public int getvalue(int sum,int wei){
int[] [] value =new int [sum][wei];
for(int i=1;i<sum;i++){
for(int j=0;j<wei;j++){
if(j<w[i-1]) value[i][j] = value[i-1][j];
else{
value[i][j] = max (value[i-1][j],value[i-1][j-w[i-1]]+v[i-1]);
}
}
}
return wei;
}public int getvalues(int sum, int wei) {
int[] value = new int[wei + 1];
for (int i = 1; i < sum + 1; i++) {
for (int j = wei; j > w[i - 1] - 1; j--) {
value[j] = value[j] > value[j - w[i - 1]] + v[i - 1] ? value[j]
: value[j - w[i - 1]] + v[i - 1];
}
}
return value[wei];
}显然第三种效果最好。










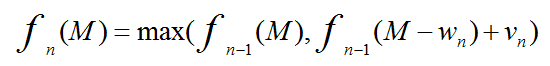














 491
491

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








