寒假蓝桥杯训练一1022 39个台阶（DFS或递归）

可以说是自己做的第一道递归题了

Problem Description

小明刚刚看完电影《第39级台阶》，离开电影院的时候，他数了数礼堂前的台阶数，恰好是39级!
站在台阶前，他突然又想着一个问题：
如果我每一步只能迈上1个或2个台阶。先迈左脚，然后左右交替，最后一步是迈右脚，也就是说一共要走偶数步。那么，上完39级台阶，有多少种不同的上法呢？
请你利用计算机的优势，帮助小明寻找答案。
要求提交的是一个整数。
注意：不要提交解答过程，或其它的辅助说明文字。

Input

无

Output

输出一个整数 

题目思路：自己一开始理解错了，以为就是简单的 递推公式f(n)=f(n-1)+f(n-2)

                 后来才发现题目中有个要求，就是要走偶数步

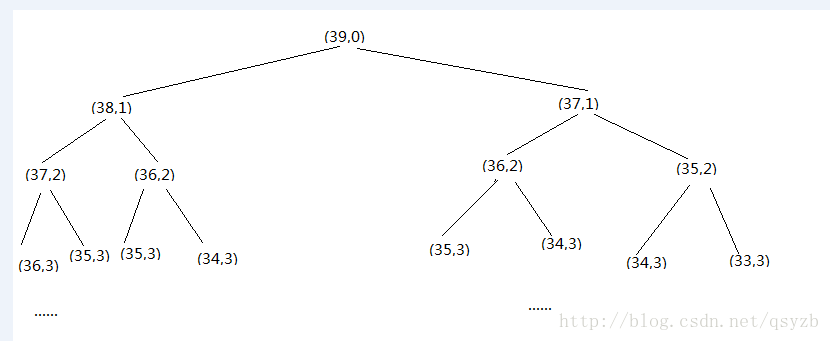
                可以有两种做法一种是 递推（如果真正理解起来本质也是DFS） 从 stairs=39,step=0  递推到 stairs=0,然后判断 step是否为偶数，如果是的话就 cnt++;

一张图就明白了

这种递归的效果如下图：

                另一种做法，直接DFS

递归：

#include<iostream>
using namespace std;
int cnt=0;
void fun(int stair,int step)//stair 表示剩余的楼梯  step 代表走过的路数 
{
	if(stair<0) return ;//假如 stair=1 的话 那么fun(stair-2,step+1); 就不予考虑 
	if(stair==0)
	{
		if(step%2==0)
			cnt++;
		return ;
	}
	fun(stair-1,step+1);//这一步走了一个台阶 
	fun(stair-2,step+1);// 这一步走了两个台阶 
}
int main()
{
	fun(39,0);
	cout<<cnt<<endl;
	return 0;
}

          

DFS

   

#include<iostream>
using namespace std;
int cnt=0;
void dfs(int m,int step)
{
	if(m>39)	return; 
	if(m==39)
	{
		if(step%2==0)
			cnt++;
			return ;	
	}
	dfs(m+1,step+1);
	dfs(m+2,step+1);
}
int main()
{
	dfs(0,0);
	cout<<cnt<<endl; 
	return 0;
}