Self-critical n-step Training for Image Captioning_self-critical image captioning-CSDN博客

本文链接：https://blog.csdn.net/luo3300612/article/details/92767986

本文聚焦图像描述的训练方法，指出传统方法存在exposure bias及训练与测试度量不一致的问题。提出advantage actor - critic algorithm估计per - token advantage，利用图像描述特性简化优势函数表达，使用n - step reformulated advantage function增加状态值均值、减小方差，还介绍了两种估计状态动作值函数的方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Self-critical n-step Training for Image Captioning

原文地址

时间：2019 CVPR

Intro

image caption 传统训练方法有两个问题

exposure bias，训练的时候使用ground truth词，测试的时候使用自己预测的词，不一致的预测方法，可能导致错误累积，称为exposure bias
训练时以交叉熵为损失函数，测试时使用metric度量，两者的不一致性

最近的研究表表明可以使用RL来直接优化metric，从而解决第二个问题

本文提出了advantage actor-critic algorithm来估计per-token advantage，且不引入有偏差的参数值估计

本文的贡献包括

利用image caption的特性，我们发现了状态值函数和它之前的状态动作值函数的关系，从而简化了优势函数的表达形式
在简化的优势函数上，我们使用了n-step reformulated advantage function 来逐渐增加状态值函数的绝对值的均值，并减小方差
我们使用了两个rollout方法来估计状态动作值函数并进行self-critical训练

Methodology

使用交叉熵训练

$a_t\in A$ 是序列中的词， $T$ 是序列长度， $I$ 是图片， $I_F$ 是图片特征，最小化交叉熵
在这里插入图片描述
其中 $\pi$ 是概率分布函数

使用策略梯度训练

问题形式化

马尔科夫过程（MDP） $\{S,A,P,R,\gamma\}$
agent,captioning model
$S$ ,state space
$A$ ,action space，字典
$P(s_{t+1}|s_t,a_t)$ 状态转移概率
$R(s_t,a_t)$ 是回报函数
$\gamma\in(0,1]$ 是衰减系数

agent选择一个action，就对应于生成一个token，从一个条件概率分布 $\pi(a|s)$ 中，称为策略，策略梯度算法中，我们考虑被 $\theta$ 参数化的策略 $\pi_\theta(a|s)$ ，状态 $s_t\in S$ 是图片特征 $I_F$ 和到目前为止的tokens/actions ${a_0,a_1,a_2,...,a_{t-1}\}$ ：
在这里插入图片描述
这个过程中，状态转移矩阵是确定的，因此

通常采取动作后，我们可以得到一个奖励值，但是在image caption问题中，奖励值只能在最终句子生成完时计算

状态值函数和状态动作值函数定义如下

强化学习的目的是通过估计策略梯度来最大化累积回报值 $V^\pi(s_0)=E_\pi[\sum^T_{t=1}\gamma^{t-1}r_t]$ ，策略梯度算法中，梯度为
在这里插入图片描述
其中 $b$ 可以是任意函数，只要它不依赖 $a_t$ ，使用 $V^\pi_{s_t}$ 作为baseline，就可以得到A2C算法

这个算法鼓励agent采用比平均动作好的动作，而抑制比平均动作差的动作

1-step reformulated advantage function，image caption是一个特殊的强化学习任务，它的状态转移矩阵是确定的，因此可以reformulate一些公式，首先
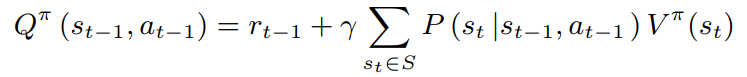
在这里插入图片描述
因为 $P$ 是确定的，所以

因为当 $t < = T$ 时， $r_{t-1}=0$ 所以

从而对于

有

因此每个状态动作值函数用它上一步的状态动作值函数作为baseline，因此称为1-step,这个方程鼓励更大的期望累积回报，抑制少的期望累积回报

最直接的模拟环境的方法就是使用Monte Carlo 轨迹 $\{(s_t,a_t,r_t)\}^T_{t=1}$ ，采样自多项分布，从而策略梯度为
在这里插入图片描述
其中 $Q$ 是 $\hat{Q}$ 的经验估计

n-step reformulated function，之前的两个方法，第一个方差较大，第二个会引入估计误差，因此我们使用n-step reformulated advantage function，使用n-step的优势函数
在这里插入图片描述
随着n的增加，per-token的优势逐渐损失了，直到 $n = T$ ，得到一个sequence level的损失

估计状态动作值函数，这里有两种估计方法，使用K Monte Carlo rollouts，或者使用inference algorithm，

在 $K$ Monte Carlo rollouts中，我们以序列 ${s_t,a_t\}$ 为起始采样 $K$ 个连续序列来得到 ${a_{t+1},a_{t+2},...,a_T\}$ ，利用多项分布来采样，当 $\gamma=1$ 时，状态动作值函数可计算为 $K$ 个回报函数的均值
在这里插入图片描述
在max-probability rollout中，我们采样一个序列来得到 ${a_{t+1},a_{t+2},...,a_T\}$ ，然后得到