[bzoj2142]礼物 扩展lucas定理

传送门

Description

一年一度的圣诞节快要来到了。每年的圣诞节小E都会收到许多礼物，当然他也会送出许多礼物。不同的人物在小E

心目中的重要性不同，在小E心中分量越重的人，收到的礼物会越多。小E从商店中购买了n件礼物，打算送给m个人

，其中送给第i个人礼物数量为wi。请你帮忙计算出送礼物的方案数（两个方案被认为是不同的，当且仅当存在某

个人在这两种方案中收到的礼物不同）。由于方案数可能会很大，你只需要输出模P后的结果。

Input

输入的第一行包含一个正整数P，表示模；

第二行包含两个整整数n和m，分别表示小E从商店购买的礼物数和接受礼物的人数；

以下m行每行仅包含一个正整数wi，表示小E要送给第i个人的礼物数量。

Output

若不存在可行方案，则输出“Impossible”，否则输出一个整数，表示模P后的方案数。

Sample Input

100
4 2
1
2

Sample Output

12
【样例说明】
下面是对样例1的说明。
以“/”分割，“/”前后分别表示送给第一个人和第二个人的礼物编号。12种方案详情如下：
1/23 1/24 1/34
2/13 2/14 2/34
3/12 3/14 3/24
4/12 4/13 4/23
【数据规模和约定】
设P=p1^c1 * p2^c2 * p3^c3 * … *pt ^ ct，pi为质数。
对于100%的数据，1≤n≤109，1≤m≤5，1≤pi^ci≤10^5。

我们将问题转化 答案应当是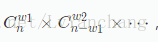，且如果要求的礼物总数超过了买的礼物，则直接输出Impossible.

那么如何求组合数的取模呢？

这里我们要引进一个非常高端的操作 扩展Lucas定理。

首先我们来看看普通的lucas定理：

lucas定理是为了解决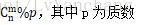。这里先放一波结论，相信各位大佬的智商一定可以秒懂QAQ

Lucas最大的数据处理能力是p在10^5左右，不能再大了，hdu 3037就是10^5级别的！

对于大组合数取模，n,m不大于10^5的话，用逆元的方法，可以解决。对于n,m大于10^5的话，那么要求p<10^5，这样就是Lucas定理了，将n,m转化到10^5以内解。

那么我们再来看看扩展Lucas定理：

扩展Lucas所解决的问题是

我们试着将问题一步步解决，先把p分解质因数。

那么如何求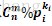呢？

于是我们最初的问题就迎刃而解啦！是不是很轻松呢！

AC代码：

#include<cstdio>
#include<iostream>
#define ll long long
using namespace std;
ll mod,n,m,w[10],ans,x,y,Pk[10002],Pi[10002],r[10002],num;
ll qpow(ll a,ll b,ll mod){//快速幂 求a^b%mod 
	ll mul=1;
	while(b){
		if(b&1){
			mul=(mul*a)%mod;
		}
		b>>=1;
		a=(a*a)%mod;
	}
	return mul;
}
ll exgcd(ll a,ll b,ll &x,ll &y){//扩展欧几里得 求ax+by=1的正整数解 
	ll d;
	if(b){d=exgcd(b,a%b,y,x);y-=a/b*x;return d;}
	x=1;y=0;return a;
}
ll inv(ll x,ll mod){//求 x在%mod下的逆元 
	ll anx,any;exgcd(x,mod,anx,any);return (anx+mod)%mod;
}
ll muli(ll n,ll pi,ll pk){//求扩展lucas定理中与pi互质的那部分的值 
	if(!n)return 1;
	ll ans=1;
	for(ll i=2;i<=pk;i++){
		if(i%pi)ans=(ans*i)%pk;
	}
	ans=qpow(ans,n/pk,pk);
	for(ll i=2;i<=n%pk;i++){
		if(i%pi)ans=(ans*i)%pk;
	}
	return ans*muli(n/pi,pi,pk)%pk;
}
ll exlucas(ll n,ll m,ll pi,ll pk){//扩展lucas 
	if(m>n)return 0;
	ll a=muli(n,pi,pk),b=muli(m,pi,pk),c=muli(n-m,pi,pk);
	ll k=0;for(ll i=n;i;)k+=i/=pi;for(ll i=m;i;)k-=i/=pi;for(ll i=n-m;i;)k-=i/=pi;
	return a*inv(b,pk)*inv(c,pk)*qpow(pi,k,pk)%pk;
}
ll crt(){//中国剩余定理合并一下 
    ll M=1,ret=0;
    for(int i=0;i<num;i++)M*=Pk[i];
	for(int i=0;i<num;i++){
		ll w=M/Pk[i];
		ret+=w*inv(w,Pk[i])*r[i];
		ret%=M;
	}
	return (ret+M)%M;
}
ll solve(){//如果不会中国剩余定理直接exgcd求模线性方程也行 
	ll M=Pk[0],R=r[0],d,c,anx,any;
	for(ll i=1;i<num;i++){
		d=exgcd(M,Pk[i],anx,any);c=r[i]-R;
		exgcd(M/d,Pk[i]/d,anx,any);anx=c/d*anx;
		R+=anx*M;
		M=M/d*Pk[i];
		R%=M;
	}
	return (R+M)%M;
}
void prep(ll n){// 分解质因数 
	for(ll i=2;i*i<=n;i++){
		if(n%i==0){
			ll pk=1;
			while(n%i==0)pk*=i,n/=i;
 			Pk[num]=pk;
 			Pi[num]=i;
 			num++;
    	}
	}
 	if(n>1)Pk[num]=n,Pi[num]=n,num++;
}
ll work(ll n,ll m){//求C(n,m)%mod 
	for(int i=0;i<num;i++){
   	    r[i]=exlucas(n,m,Pi[i],Pk[i]);
	}
 	return crt();
}
int main(){
	scanf("%lld%lld%lld",&mod,&n,&m);
	ll sum=0;
	for(int i=1;i<=m;i++){
		scanf("%lld",&w[i]);
		sum+=w[i];
	}
	if(n<sum){printf("Impossible\n");return 0;}
	prep(mod); 
	ans=1;
	for(int i=1;i<=m;i++){
		n-=w[i-1];
		ans=ans*work(n,w[i])%mod;
	}
	printf("%lld\n",ans);
	return 0;
}