「回溯算法」问题选讲-5（使用「回溯算法」玩游戏）（自己的草稿，内容不严谨，与之前有重复，不用看）

「回溯算法」由于它是一个遍历算法，再加上通常情况下，我们使用一份状态变量去搜索整个「状态空间」，因此「回溯算法」很多时候能够帮助我们解决一些游戏类的问题。

因为人脑是很难穷举玩所有可能的情况，但是我们可以借助编程语言，来帮助我们玩好一些游戏，因此，在一些人工智能的书籍上，很多时候会先介绍回溯算法，可以认为「回溯算法」是人工智能的基础算法。

下面我们就来看一个典型的使用「回溯算法」解决的问题：「n 皇后」问题，这道题是「力扣」上第 51 号问题。

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

输入: 4
输出: [
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

分析：以 4 皇后问题为例，它的「搜索」过程如下，大家完全可以在纸上模拟下面这个过程：

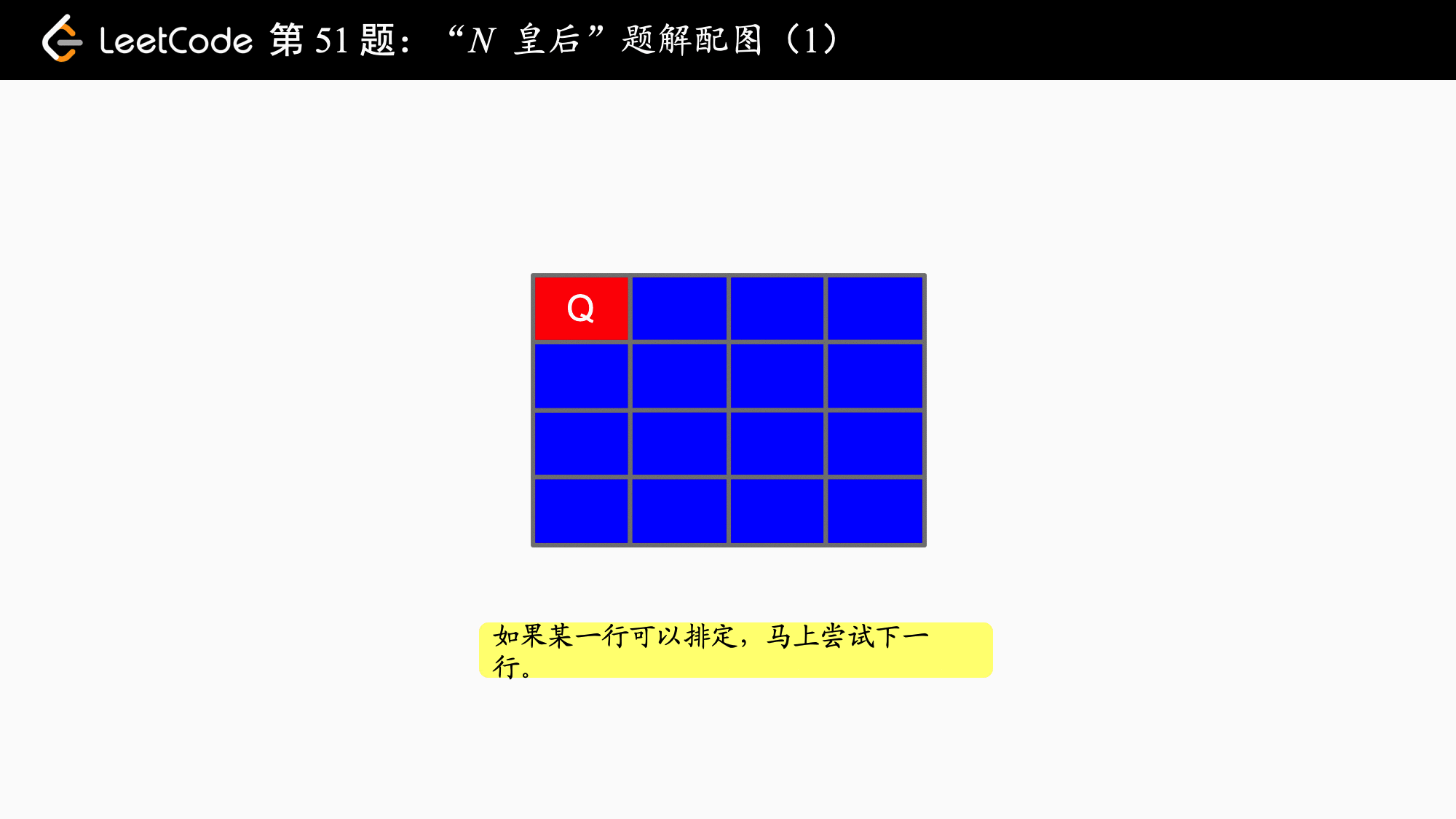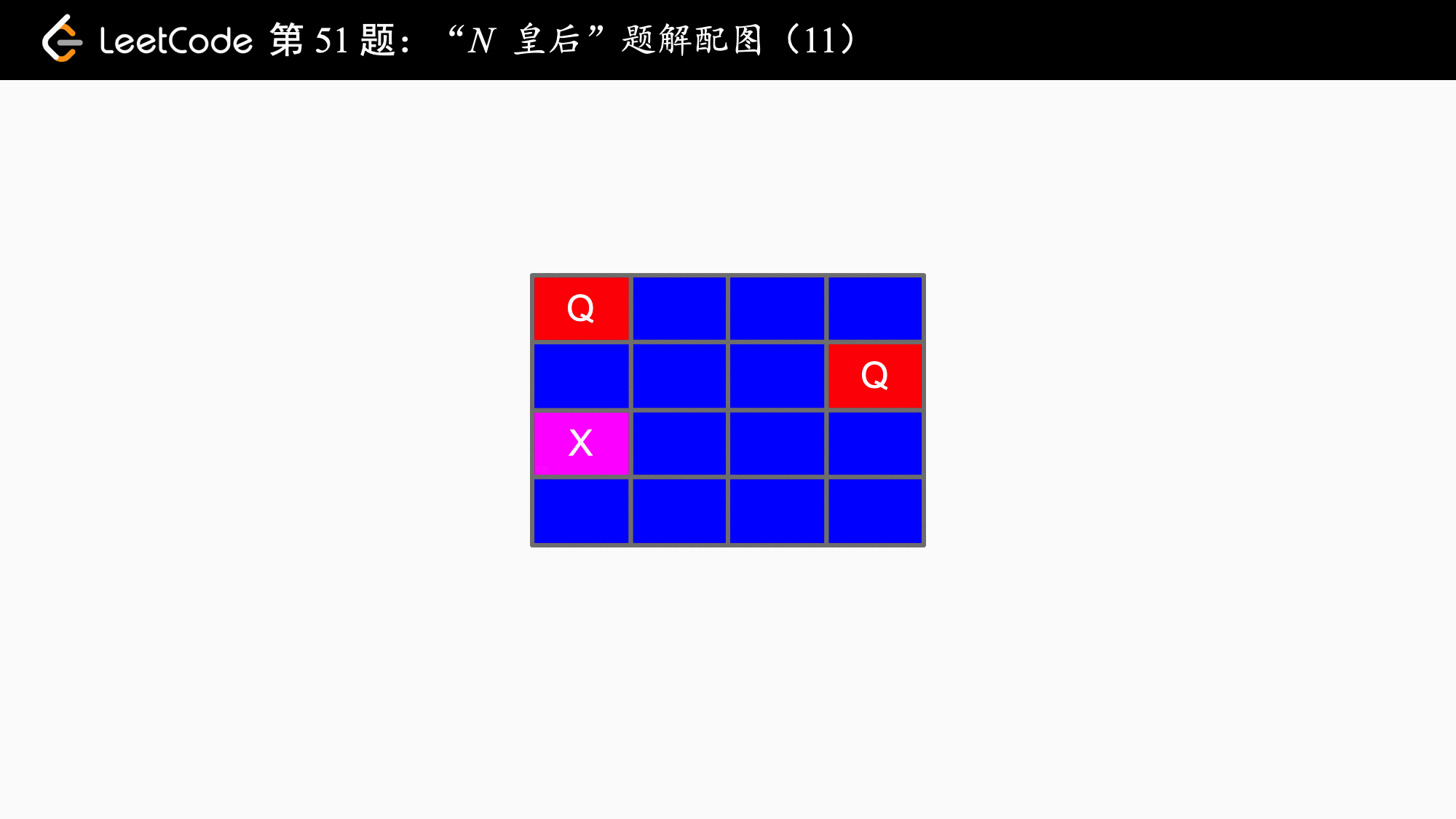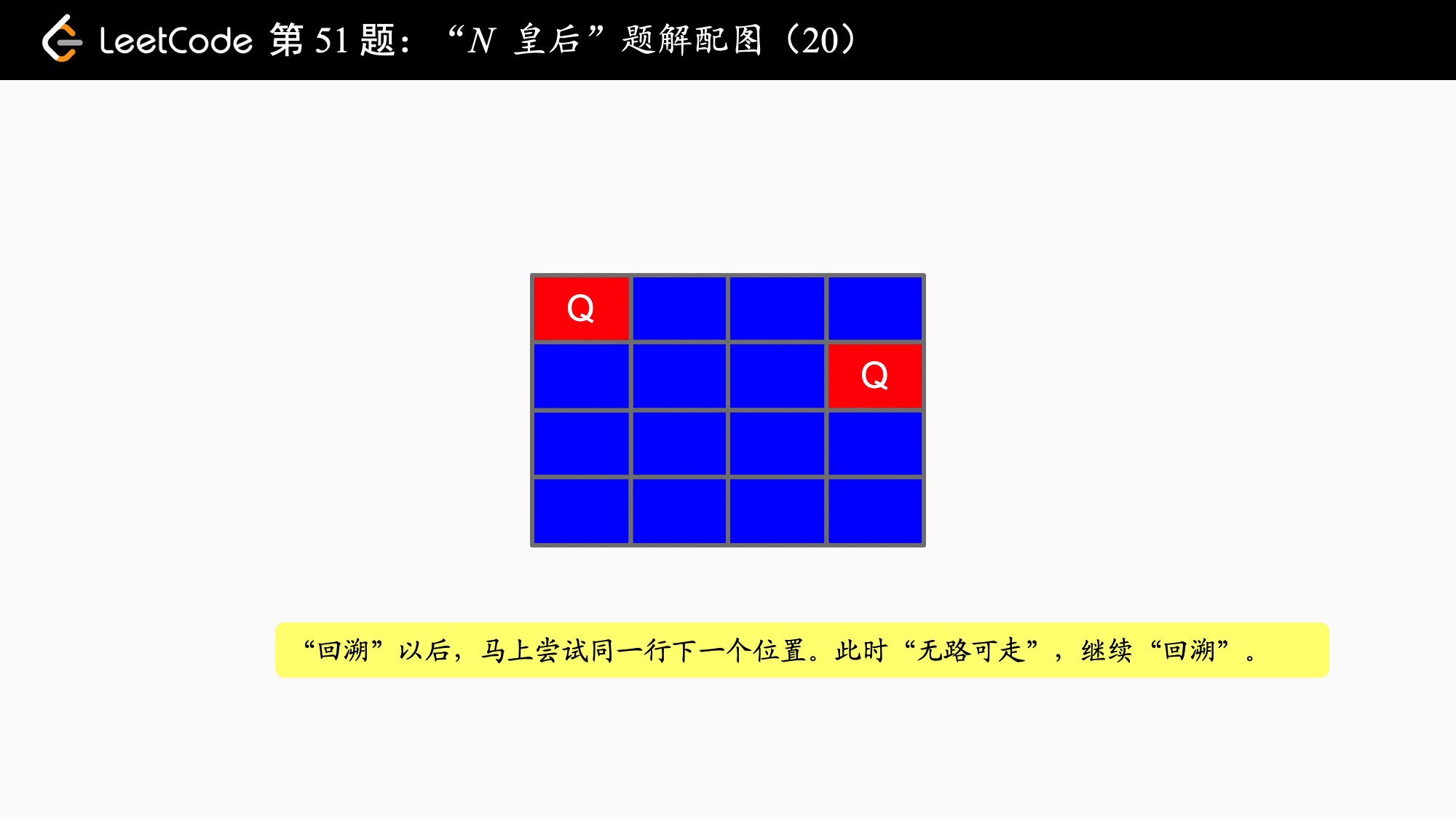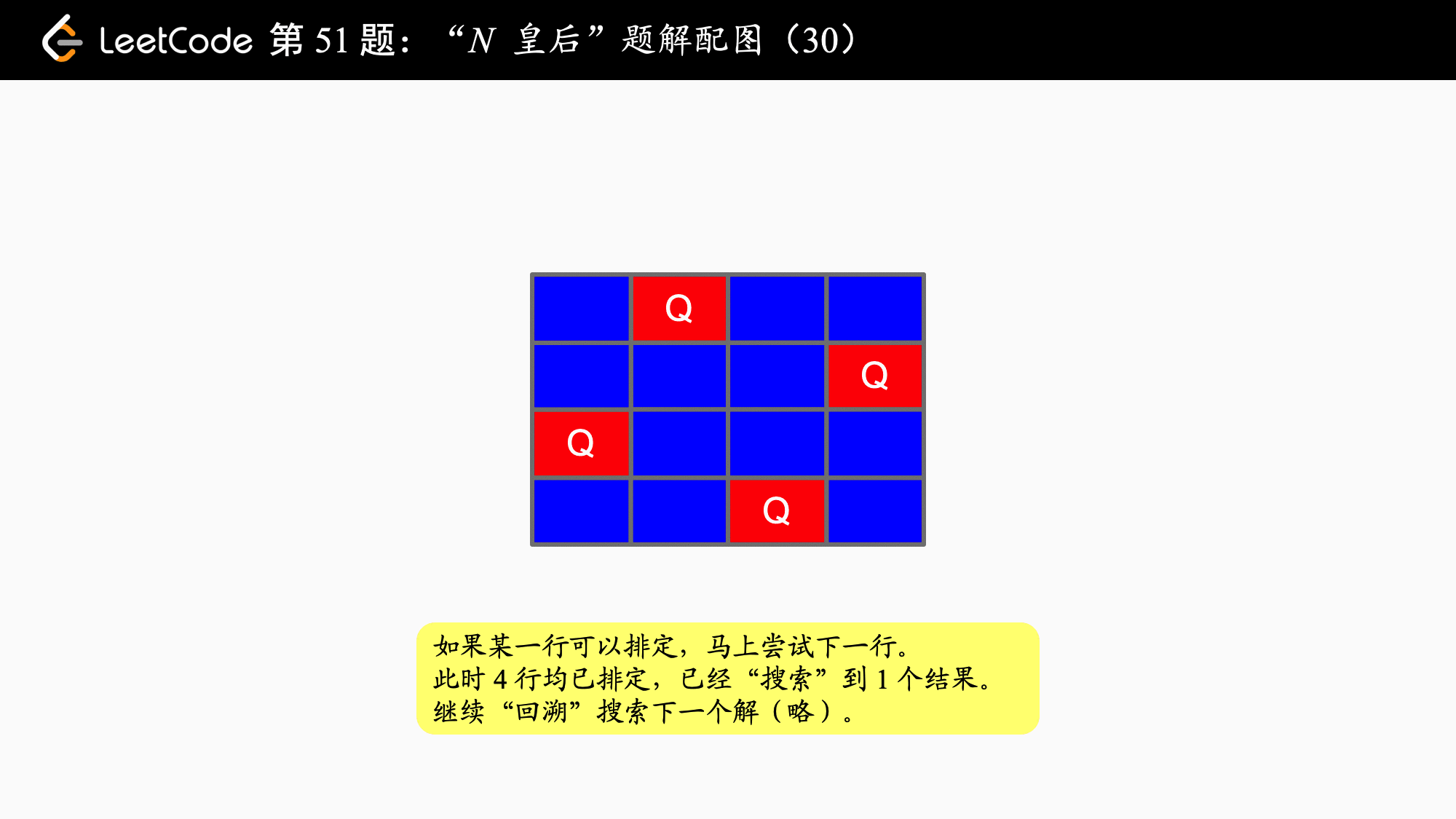{:width=500}
搜索问题的解决策略是画递归树。还以 4 皇后问题为例，画出的递归树如下。

以下假定给棋盘的每一行从左到右标记为 $1$ 、 $2$ 、 $3$ 、 $4$ ：

{:align=center}

那么，递归搜索的过程可以表示成如下递归树（只画了 2 层）：

{:width=600}
这其实就是「全排列」问题 + 「剪枝」。「剪枝」的依据就是题目中描述的「N 皇后」问题的规则，有了使用数组 used （哈希表、位图）的经验，我们可以多设置一些「状态」，下面依次进行分析：

由于是一行一行摆放，因此这些「皇后」一定不在同一行，无需额外设置状态；
为了保证不再同一列，即不能出现 [2, 2, 1, 3] 这种情况，第 46 的数组 used（哈希表、位图）就是这样的「状态」变量；
为了保证至少两个皇后不同时出现在主对角线或者副对角线，我们的策略是，只要「检测」到新摆放的「皇后」与已经摆放好的「皇后」冲突，就尝试摆放下一个位置，在「无处安放」的时候「剪枝」。

下面我们研究一下主对角线或者副对角线上的元素有什么特性。我们此时能掌握的信息只有行和列的索引，不妨将它标注在棋盘上。

为此，我们可以像数组 used 那样，再为「主对角线」和「副对角线」设置相应的数组变量，只要排定一个「皇后」的位置，就相应低占住相应的位置；
因为位置有限，可以使用数组，不过我个人先使用的哈希表，原因是副对角那里使用数组的话还要计算一个偏差，另外，数组的元素个数也要归纳得到，因此，使用哈希表表示「状态」，我认为在编码上是比较简洁的；
写对了「哈希表」以后，说明我们的思路是没有问题的，然后再写「数组」作为状态，最后写「位图」作为「状态」。

得到一个符合要求的「全排列」以后，生成棋盘的代码就很简单了。

**参考代码 **：使用哈希表分别记录「列占用情况」、「主对角线占用情况」、「副对角线占用情况」。

Java 代码：

import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;
import java.util.Set;
import java.util.Stack;

public class Solution {

    public List<List<String>> solveNQueens(int n) {
        List<List<String>> res = new ArrayList<>();
        if (n == 0) {
            return res;
        }

        int[] nums = new int[n];
        for (int i = 0; i < n; i++) {
            nums[i] = i;
        }

        boolean[] col = new boolean[n];
        boolean[] master = new boolean[2 * n - 1];
        boolean[] slave = new boolean[2 * n - 1];
        Stack<Integer> stack = new Stack<>();

        backtrack(nums, 0, n, col, master, slave, stack, res);
        return res;
    }

    private void backtrack(int[] nums, int row, int n,
                           boolean[] col,
                           boolean[] master,
                           boolean[] slave,
                           Stack<Integer> stack,
                           List<List<String>> res) {

        if (row == n) {
            List<String> board = convert2board(stack, n);
            res.add(board);
            return;
        }

        // 针对每一列，尝试是否可以放置
        for (int i = 0; i < n; i++) {
            if (!col[i] && !master[row + i] && !slave[row - i + n - 1]) {
                stack.add(nums[i]);
                col[i] = true;
                master[row + i] = true;
                slave[row - i + n - 1] = true;

                backtrack(nums, row + 1, n, col, master, slave, stack, res);

                slave[row - i + n - 1] = false;
                master[row + i] = false;
                col[i] = false;
                stack.pop();
            }
        }
    }

    private List<String> convert2board(Stack<Integer> stack, int n) {
        List<String> board = new ArrayList<>();
        for (Integer num : stack) {
            StringBuilder stringBuilder = new StringBuilder();
            for (int i = 0; i < n; i++) {
                stringBuilder.append(".");
            }
            stringBuilder.replace(num, num + 1, "Q");
            board.add(stringBuilder.toString());
        }
        return board;
    }
}