Codeforces Rockethon 2015

最新推荐文章于 2024-04-05 10:50:56 发布

TaoSama

最新推荐文章于 2024-04-05 10:50:56 发布

阅读量565

点赞数

分类专栏：搜索文章标签： codeforces

本文链接：https://blog.csdn.net/lwt36/article/details/43639191

版权

搜索专栏收录该内容

20 篇文章 0 订阅

订阅专栏

Two players play a simple game. Each player is provided with a box with balls. First player's box contains exactly n1 balls and second player's box contains exactly n2 balls. In one move first player can take from 1 to k1 balls from his box and throw them away. Similarly, the second player can take from 1 to k2 balls from his box in his move. Players alternate turns and the first player starts the game. The one who can't make a move loses. Your task is to determine who wins if both players play optimally.

Input

The first line contains four integers n1, n2, k1, k2. All numbers in the input are from 1 to 50.

This problem doesn't have subproblems. You will get 3 points for the correct submission.

Output

Output "First" if the first player wins and "Second" otherwise.

   Sample test(s) 
 
     input 
   
2 2 1 2

     output 
   
Second

     input 
   
2 1 1 1

     output 
   
First

Note

Consider the first sample test. Each player has a box with 2 balls. The first player draws a single ball from his box in one move and the second player can either take 1 or 2 balls from his box in one move. No matter how the first player acts, the second player can always win if he plays wisely.

= = 水的不能再水的题目~ 因为是随便拿~ 所以每个人每次都拿1就是最优的那么结果就显而易见了

AC代码如下：

//
//  A.Game
//
//  Created by TaoSama on 2015-02-08
//  Copyright (c) 2014 TaoSama. All rights reserved.
//
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>
#define CLR(x,y) memset(x, y, sizeof(x))

using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int N = 1e5 + 10;

int n1,n2,k1,k2;

int main() {
#ifdef LOCAL
	freopen("in.txt", "r", stdin);
//	freopen("out.txt","w",stdout);
#endif
	ios_base::sync_with_stdio(0);

	while(cin>>n1>>n2>>k1>>k2){
		if(n1>n2) cout<<"First"<<endl;
		else      cout<<"Second"<<endl;
	}

	return 0;
}

You are given a permutation p of numbers 1, 2, ..., n. Let's define f(p) as the following sum:

$\text{[math]}$

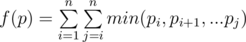
Find the lexicographically m-th permutation of length n in the set of permutations having the maximum possible value of f(p).

Input

The single line of input contains two integers n and m (1 ≤ m ≤ cntn), where cntn is the number of permutations of length n with maximum possible value of f(p).

The problem consists of two subproblems. The subproblems have different constraints on the input. You will get some score for the correct submission of the subproblem. The description of the subproblems follows.

In subproblem B1 (3 points), the constraint 1 ≤ n ≤ 8 will hold.
In subproblem B2 (4 points), the constraint 1 ≤ n ≤ 50 will hold.

Output

Output n number forming the required permutation.

    Sample test(s) 
  
      input 
    
2 2

      output 
    
2 1 

      input 
    
3 2

      output 
    
1 3 2

Note

In the first example, both permutations of numbers {1, 2} yield maximum possible f(p) which is equal to 4. Among them, (2, 1) comes second in lexicographical order.

对于B1 = = 自己实在是弱啊用了一堆标准库函数用next_permutation来求1-n的全排列然后暴力按照公式算出每个值

然后排序找到最大值的第m个字典序的序列打印就好了

AC代码如下：

//
//  B1.Permuatation
//
//  Created by TaoSama on 2015-02-08
//  Copyright (c) 2014 TaoSama. All rights reserved.
//
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>
#define CLR(x,y) memset(x, y, sizeof(x))

using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int N = 1e5 + 10;

int n, m;
bool cmp(pair<int, int> x, pair<int, int> y) {
	if(x.first == y.first) return x.second < y.second;
	return x.first > y.first;
}
int main() {
#ifdef LOCAL
	freopen("in.txt", "r", stdin);
//	freopen("out.txt","w",stdout);
#endif
	ios_base::sync_with_stdio(0);

	while(cin >> n >> m) {
		vector<int> a, b[N];
		vector<pair<int, int> > ans;
		for(int i = 1; i <= n; ++i) a.push_back(i);
		int t = 1; b[1] = a;
		while(next_permutation(a.begin(), a.end()))
			b[++t] = a;

		for(int i = 1; i <= t; ++i) {
			int sum = 0;
			for(int j = 0; j < n; ++j) {
				for(int k = j; k < n; ++k) {
					int Min = INF;
					for(int l = j; l <= k; ++l)
						Min = min(Min, b[i][l]);
					sum += Min;
				}
			}
			ans.push_back(make_pair(sum, i));
//			cout << sum << ' ' << i << endl;
		}
		sort(ans.begin(), ans.end(), cmp);
		int x = ans[m - 1].second;
		for(int i = 0; i < n - 1; ++i)
			cout << b[x][i] << ' ';
		cout << b[x][n - 1] << endl;
	}
	return 0;
}

这个是我同学给我发的图他给我讲解的观察上方的图片可以发现 12->(123,132) 然后 123->(1234, 1243) 132->(1342, 1432)

至于最后一个不用我说你们也该明白了 1个变2个那么我们可以得到最大值解的数量是2^(n-1)个

我们观察新数n的插入位置在3中分别是在3和2 在4中分别是4和3

那么我们所求的dfs(n,m)的插入位置应该是 dfs(n-1, (x+1)>>1) + (x&1) 发现n,m的中奇数项的插入位置是n-1对应项位置+1 偶数项则不变

如此一来递归求解即可复杂度为O(n^2)

AC代码如下：

//
//  B2.Permutation
//
//  Created by TaoSama on 2015-02-08
//  Copyright (c) 2015 TaoSama. All rights reserved.
//
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>
#define CLR(x,y) memset(x, y, sizeof(x))

using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int N = 1e5 + 10;

int n, a[55]; long long m;

int dfs(int dep, long long x) {
	if(dep == 1) return 1;
	int cur = dfs(dep - 1, (x + 1) >> 1) + (x & 1);
	for(int i = dep; i >= cur+1 ; --i)
		a[i] = a[i - 1];
	a[cur] = dep;
	return cur;
}

int main() {
#ifdef LOCAL
	freopen("in.txt", "r", stdin);
//	freopen("out.txt","w",stdout);
#endif
	ios_base::sync_with_stdio(0);

	while(cin >> n >> m) {
		a[1] = 1;
		dfs(n, m);
		for(int i = 1; i < n; ++i)
			cout << a[i] << ' ';
		cout << a[n] << endl;
	}
	return 0;
}

还有一个O(n)求解的姿势 - - 恕我没看懂题解也没看懂tourist的代码只把它附在这里好了

int ans[777];

int main() {
	int n; long long m;
	cin >> n >> m;
	int l = 0, r = n - 1;
	for(int j = n - 1; j > 0; j--) {
		if(m <= (1LL << (j - 1))) {
			ans[l++] = n - j;
		} else {
			ans[r--] = n - j;
			m -= (1LL << (j - 1));
		}
	}
	ans[l] = n;
	for(int i = 0; i < n; i++) cout << ans[i] << " ";
	cout << endl;
	return 0;
}