极限值的若干方法-详解（I）

题目1.3与参考答案取自《数学分析中的经典问题与方法》斐礼文第三版P24-42，详细解析为个人思考写得。

IDEA 一.等价替换与初等变形

等价替换

常用的等价替换公式（不必记忆，以多用的方式去记忆）：

x -> 0时，

（1） (a>0 & b ≠ 0)

（2）

课本与教程往往没有给出详细证明，但实际也很简单，本质就是等价无穷小的证明：

初等变形

所谓的初等变形，就是比如三角函数的变形、平方差、整数累和、经典递推公式。

一般这种题目有时不单纯考初等变形，还会结合等价替换一起考察。

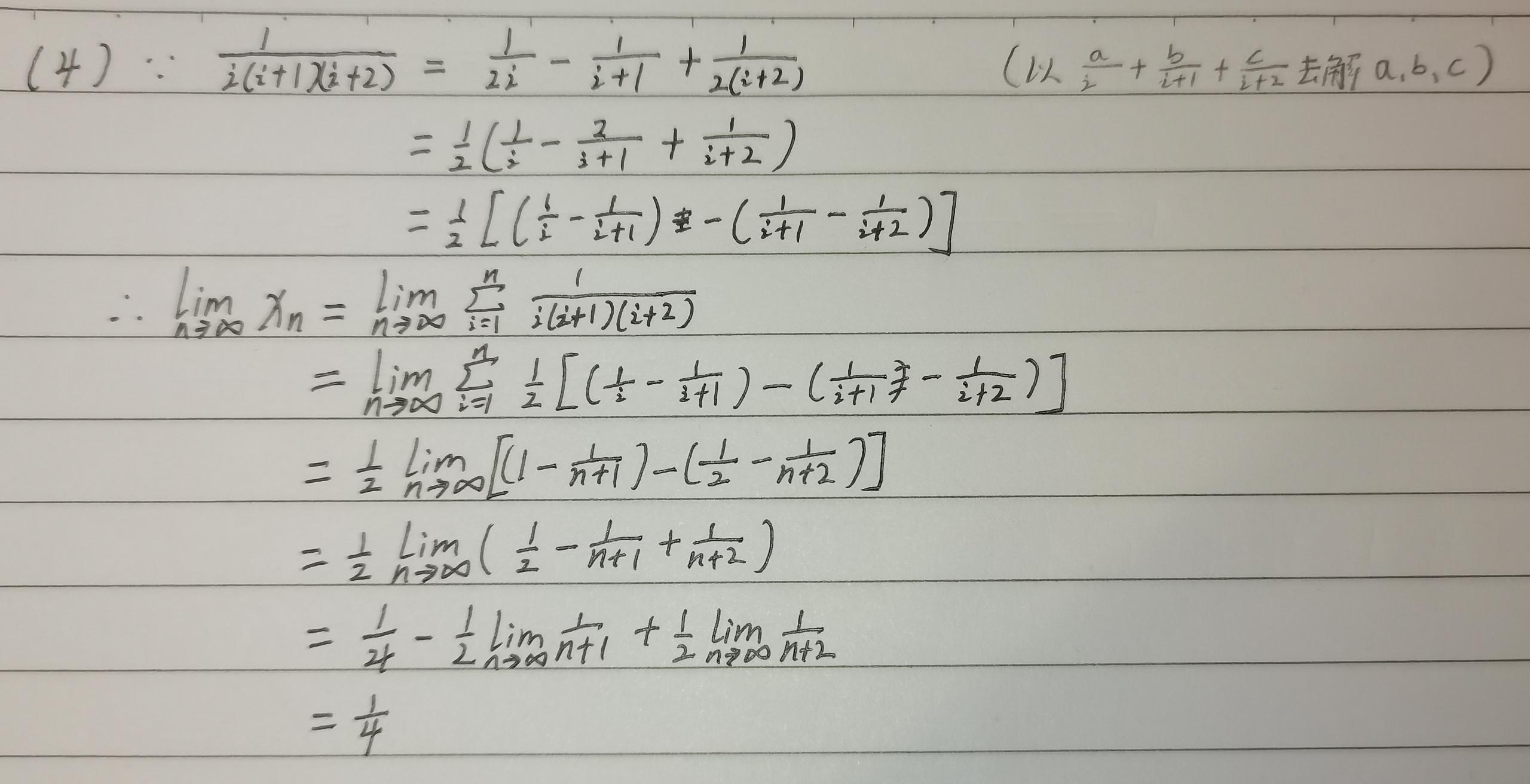
IDEA 二.利用已知极限

利用一些已知的极限式子或极限推导式子。