BST二叉查找树

博客链接：http://blog.csdn.net/lyh__521/article/details/49811149

介绍

如图1就是一颗二叉排序树，也就是二叉查找树，又称二叉搜索树，简称BST

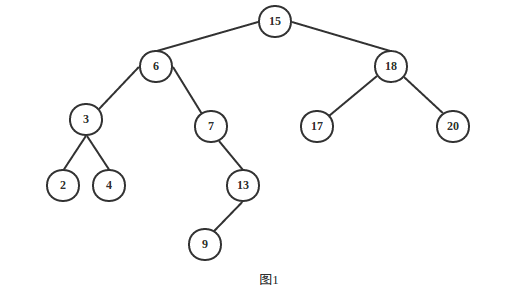
• 二叉排序树包含以下域：

成员	含义
left	指向左孩子
right	指向右孩子
key	关键字
parent	指向父结点

---

• 特点

设 x 为二叉排序树中的一个结点。如果y是x的左子树中的一个结点，则( y->key) <= (x->key);如果y是x的右子树中的一个结点，则(y->key) >= (x->key)。

即任意一个结点的左子树的所有关键字都比他小，右子树的所有关键字都比他大。

---

• 关键字有序性

使用中序遍历算法可将一棵BST树的所有关键字按照从小到大的顺序输出。

//中序遍历
void INORDER_Tree_Walk(BS_Tree* root)
{
    if(root != NULL)
    {
         INORDER_Tree_Walk(root->left);  //遍历左子树
         print(root->key);               //输出关键字
         INORDER_Tree_Walk(root->right); //遍历右子树
    }
}

---

查询二叉查找树

  从根结点开始查找，对经过的每个结点 x 与 要查询的k 比较，如果 k < (x->key) ,则沿着左子树下降;如果 k > (x->key) ,则沿着右子树下降 。未找到，返回NULL。
  所以查找操作最多不会大于树的高度。时间复杂度为O(h),h为树的高度。

例如：查找 13

• 递归查找

BS_Tree*  Tree_Search(BS_Tree* root,int k)
{
    //碰到空结点 或 查询成功
    if(root == NULL || k == root->key )
        return x;
    //大于要查询的关键字
    else if(k < root->key)
    //走向左子树
        return Tree_Search(root->left,k); 
    else
    //走向右子树
        return Tree_Search(root->right,k);
}

• 非递归查找

BS_Tree* ITERATIVE_Tree_Search(BS_Tree* root,int k)
{
    BS_Tree*     x = root;
    while(x != NULL && k != x->key)
    {
        if(k < x->key)
            x = x->left;
        else
            x = x->right;
    }
    return x;
}

---

最大关键字

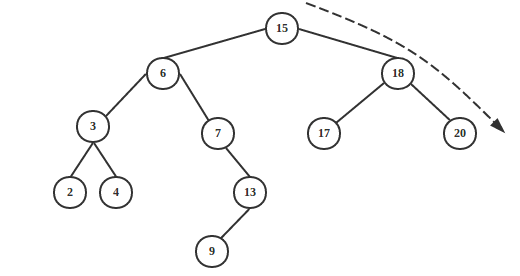
  如果要查找整棵二叉查找树的最大关键字，只要从根结点开始，一直沿着各结点的right 指针（向右）走即可。

如下图：

//最大关键字
BS_Tree* Tree_MAXIMUM(BS_Tree* x)
{
    //从 x 结点出发
    while(x->right != NULL)
        x = x->right; //走向右子树

    return x;
}

最小关键字

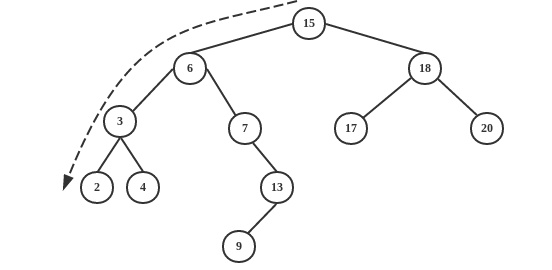
  如果要查找整棵二叉查找树的最小关键字，只要从根结点开始，一直沿着各结点的left 指针（向左）走即可。

如下图：

//最小关键字
BS_Tree* Tree_MINIMUM(BS_Tree* x)
{
    while(x->left != NULL)
        x = x->left;

    return x;
}

---

前趋与后继

• 后继

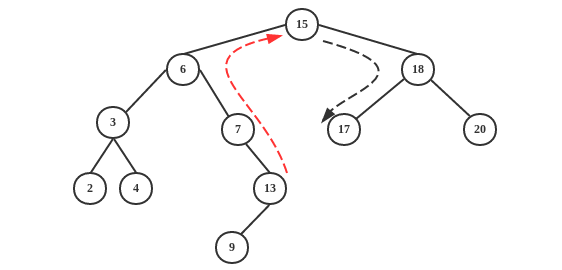
   有时我们需要找到某一个结点 x 的后继结点，即下一个大于 x 关键字的结点。因为结点右子树的所有关键字都比他大，所以如果 x 有右子树，只需要找出右子树的最小关键字。如果x 没有右子树，因为结点的所有左子树的关键字都偏小，所以我们只需要沿着 x 的父结点不断向上找，直到找到一个结点 y ,使得 x 属于 y 的左子树即可，此时y 是 x 的后继。如果返回NULL，说明 x->key 已经是树的最大关键字了。

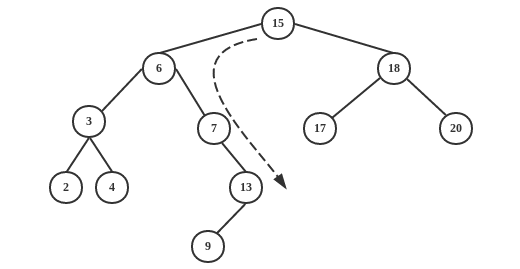
例如，下图分别查找13（没有右子树）和15的后继：13–>15 、15–>17

//后继
BS_Tree* Tree_SUCCESSOR(BS_Tree* x)
{
    if(x->right != NULL)               //x有右子树
        return Tree_MINIMUM(x->right); //返回右子树的最小关键字
    BS_Tree*  y = x->parent;     
    while(y != NULL && x == y->right)  //x 不属于父结点的左子树
    {
        x = y;                         //x 上移到父结点的位置
        y = y->parent;
    }
    return y;
}

• 前趋

即前一个比 x 小的关键字为 x 的前趋。可以模仿求后继的方法。

---

插入

插入比较简单，跟着代码注释走一遍就懂了。

//插入
void Tree_Insert(BS_Tree* root,BS_Tree* z)
{
    BS_Tree*    p = NULL;
    BS_Tree*    x = root;     //从根结点开始查找
    while(x != NULL)          //x 没走到尽头
    {
        p = x;                //p 始终指向x的父结点
        if(z->key < x->key)   //当前结点大于插入值
            x = x->left;      //x 向左转前进
        else
            x = x->right;     //x 向右转前进
    }
    z->parent = p;
    if(p == NULL)             //这是一棵空树
        root = z;             //设置新插入的结点为根结点
    else if(z->key < p->key)  
        p->left = z;          //将z 插入到左边
    else
        p->right = z;         //将z 插入到右边
}

   从根结点开始，沿树下降，指针 x 跟踪了这条路径，而 p 始终指向 x 的父结点。如果是空树，直接将插入的结点设置为根结点。否则，根据插入值与 x->key 比较的结果，决定继续向左走还是向右走，直到 x 变为NULL,NULL的位置就是我们要插入的位置。

---

删除

因为要保持二叉查找树的性质，删除操作略有点麻烦。

根据要删除结点 z 的位置，主要分为以下3种情况：

---

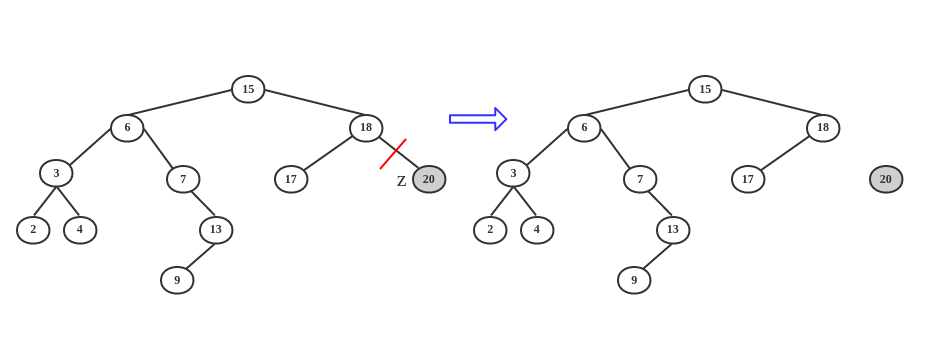
• 情况1 ： z 没有左孩子和右孩子

直接删除 z 结点，将 z 所在的位置置为NULL。

---

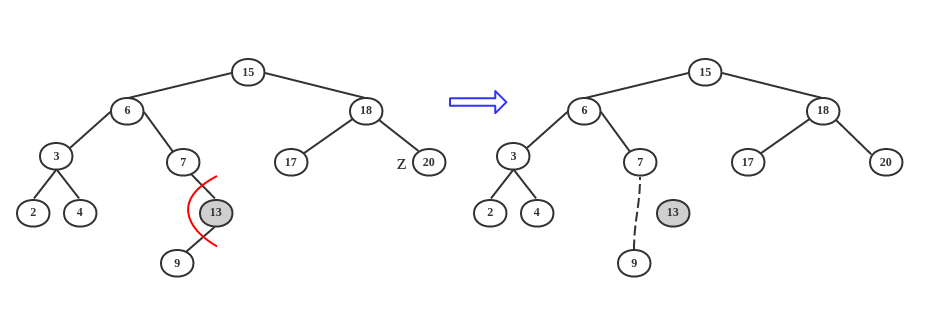
• 情况2 ：z 只有一个孩子（左孩子或者右孩子）
  

只需要直接删除 z ,让 z 的孩子与 z 的父结点相连。将 z 的孩子移到 z 原来的位置即可。

---

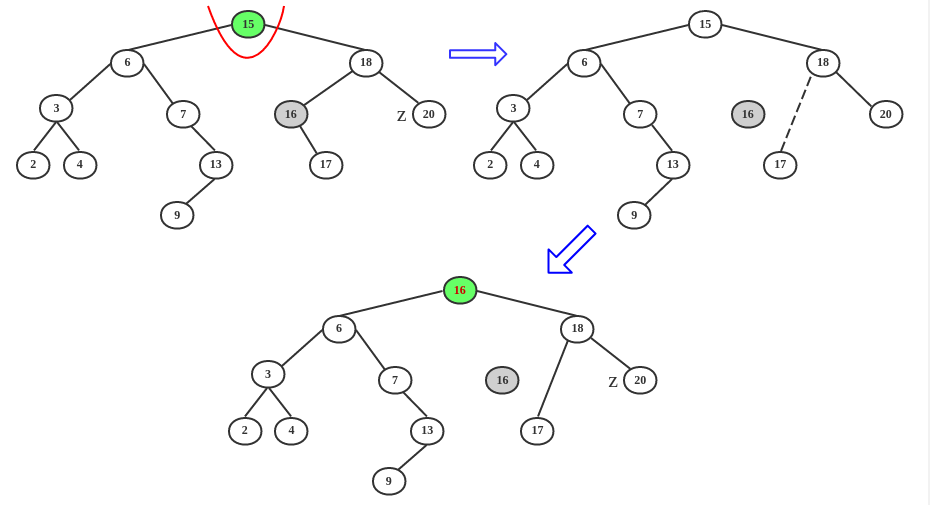
• 情况3：z 既有左孩子，又有右孩子

当 z 结点有两个孩子时，不会直接删掉 z ,而是找到 z 的后继结点，用后继结点的关键字替换掉 z 的关键字，并且删掉后继结点，如上图。因为后继结点 z 的右子树的最小关键字，用 后继替换 z ,就依然能保证 z 位置的左子树偏小，右子树偏大的性质。删掉后继结点的方法使用情况1 或 情况 2。

BS_Tree*  Tree_Delete(BS_Tree* root,BS_Tree* z)
{
    if(z->left == NULL || z->right == NULL) //没孩子或有一个孩子
        BS_Tree*  y = z;
    else
        y = Tree_SUCCESSOR(z);              //z 有两个孩子时求后继
                                            //y 指向真正要删除的结点

    if(y->left != NULL)                     //如果y有左子树
        BS_Tree*  x = y->left;              //x 指向左树
    else                                    
        x = y->right;                       //x 指向右树
                                            //y没有孩子时，x=NULL

    if(x != NULL)                           //如果y有一个孩子
        x->parent = y->parent;         //设置y的孩子的父亲为y的父结点

    if(y->parent == NULL)              //要删除的是根，必只有一个孩子
        root = x;                           //设置孩子为新的根
    else if(y = (y->parent)->left)          //否则如果y是左树
        (y->parent)->left = x;              //设置y的孩子x为左树
    else
        (y->parent)->right = x;

    if(y != z)                              //如果y是后继
        z->key = y->key;                    //用y的关键字替换z
    return y;                               //返回真正删除的位置
}

因为只有 z 有两个孩子时才需要求后继结点，那么 z 此时必然是有右孩子的，所以z 的后继结点是 z 右树的最小关键字。不存在求后继时需要沿着父结点上升的情况。

---