带你轻松掌握动态规划问题精髓

简介

动态规划（Dynamic Programming）是一种解决复杂问题的方法，通过将问题分解成更小的子问题来求解，然后将子问题的解合并起来得到原问题的解。动态规划通常用于优化问题，可以在不重复计算相同子问题的情况下高效地解决问题

动态规划最关键的就是找出状态转移方程，即相同问题在不同规模下的关系

寻找状态转移方程的一般性步骤

1. 找到相同问题（重叠子问题）相同问题必须能适配不同规模
2. 找到重叠子问题之间的关系
3. 找到重叠子问题特殊解

下面通过斐波那契数列进一步了解动态规划

斐波那契数列

斐波那契数列，前几项为0、1、1、2、3、5、8、13等。斐波那契数列中的每一项（除了前两项外）都是前两项之和

状态转移方程：

// 当n>2
dp(n) = dp(n-1) + dp(n-2)

// 当n<=2
dp(n) = 1

问题：求斐波那契数列第n项的值

代码实现

const fibonacci = (n) => {
    if(n <= 2) return 1
    let p1 = 1, p2 = 1, r = 1
    for (let i = 2; i < n; i++) {
        r = p1 + p2
        p2 = p1
        p1 = r
    }
    return r
}
console.log(fibonacci(2)) // 1
console.log(fibonacci(6)) // 8

函数定义：这段代码定义了一个名为 fibonacci 的箭头函数，接受一个整数 n 作为参数

边界条件处理：在函数内部，首先判断如果 n 小于等于 2，则直接返回 1。因为斐波那契数列从第三项开始，每一项都是前两项之和

迭代计算：接着定义了三个变量 p1、p2 和 r，分别表示斐波那契数列中的第 i-2、i-1 和 i 项。初始时，p1 和 p2 均为 1，r 初始值也为 1

循环计算：通过 for 循环从第 2 项开始计算第 n 项的斐波那契数。在每一次循环中，r 更新为 p1 和 p2 的和，同时更新 p2 为原来的 p1，p1 为新的 r。这样依次迭代计算直到计算出第 n 项的斐波那契数值

返回结果：最后返回计算得到的第 n 项斐波那契数的值 r

这种方式实现空间复杂度为 O(1)，时间复杂度为 O(n)

不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）

问总共有多少条不同的路径？

示例

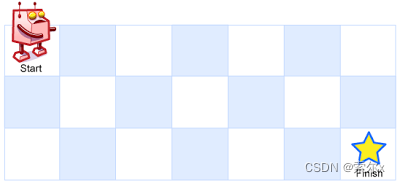
输入： m = 3, n = 7
输出： 28

分析状态转移方程

dp(i, j) 到达第i行第j列共有多少条路径，用来表示最终解和普通解

dp(i, j) = dp(i - 1, j) + dp(i, j - 1) 到达最终解的路径有两条，分别是左侧和上侧的位置

dp(i, j) = 1 特殊解，当i == 0 或 j == 0时第一行和第一列最短路径为1

代码实现

递归

const uniquePaths = (m, n) => {
    const cache = {} // 存储计算过的数据 防止重复计算
    const dp = (i, j) => {
        if(i === 1 || j === 1) {
            return 1
        }
        const key = `${i}-${j}`
        if(cache[key]) {
            return cache[key]
        }
        return cache[key] = dp(i, j - 1) + dp(i - 1, j)
    }
    return dp(m - 1, n - 1)
}

函数定义：代码定义了一个名为 uniquePaths 的箭头函数，接受两个参数 m 和 n，分别表示行数和列数

cache 对象：在函数内部定义了一个空对象 cache，用于存储已经计算过的路径数量，防止重复计算

递归函数 dp：定义了一个名为 dp 的递归函数，接受两个参数 i 和 j，分别表示当前位置的行号和列号

基本情况处理：在递归函数中，首先判断如果当前位置的行号为 1 或列号为 1，则说明只有一种路径可以到达这个位置，即返回 1

使用缓存加速计算：接着构造一个字符串 key，用来表示当前位置的唯一标识。如果 cache 中已经存在该 key 对应的值，则直接返回该值

递归计算路径数量：在没有缓存的情况下，通过递归调用自身，计算当前位置上方和左侧位置的路径数量之和。同时将结果存入 cache 对象中以备将来使用

返回结果：最终返回从起点到终点的唯一路径数量，即调用 dp 函数传入 (m-1, n-1) 的位置作为起点

循环

可以利用二维数组存储计算过程中的值，初始化第一列和第一行为1，然后遍历每个位置，计算其值为上面位置和左边位置的值之和

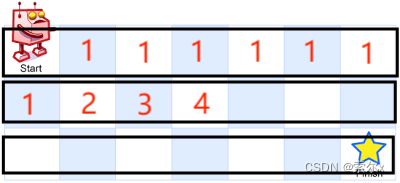
代码实现

const uniquePaths = (m, n) => {
    const dp = []
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if(i === 0 || j === 0) {
                dp[i][j] = 1
            } else {
                dp[i][j] = dp[i - 1, j] + dp[i, j - 1]
            }
        }
    }
    return dp[m - 1][n - 1]
}

定义二维数组：代码定义了一个空的二维数组 dp 用于存储计算过程中的结果，该二维数组将用来保存从起点到每个位置的唯一路径数量

动态规划计算：通过两层嵌套的循环遍历所有的行和列，对每个位置进行计算其唯一路径数量

基本情况处理：在每次遍历中，如果当前位置位于第一行或第一列（即 i 或 j 等于 0），则直接将该位置的路径数量设为 1，因为在第一行和第一列上只有一条路径可以到达该位置

动态规划转移方程：对于其他位置 (i, j)，其唯一路径数量可以根据其上方位置 (i-1, j) 和左侧位置 (i, j-1) 的唯一路径数量之和得到。因此，根据动态规划的转移方程 dp[i][j] = dp[i-1][j] + dp[i][j-1]，计算当前位置的唯一路径数量

返回结果：最后返回终点位置 (m-1, n-1) 处的唯一路径数量，即为问题的解

利用滚动数组优化空间复杂度

上面的示例在代码运行的过程会产出m个数据，每个数组中有n个元素，空间复杂度为O(m*n)

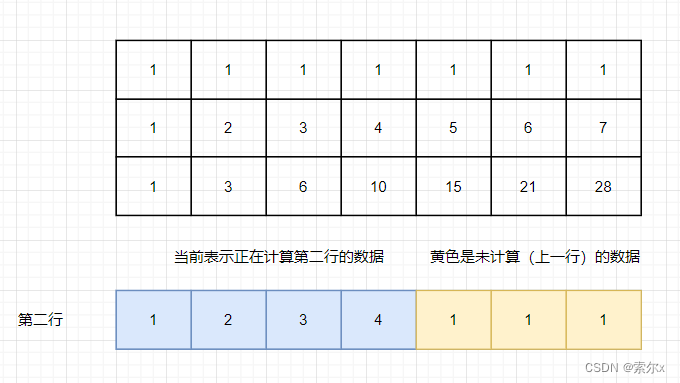
对整个数据分析过后发现一个规律，用一个数组表示当前数组，初始化的时候生成一个长度为n的数组，在计算第m行的时候就取前一项（左侧）的值和当前数组（上侧）的值，这种数组称为滚动数组，利用滚动数组降维打击后空间复杂度优化为O(n)

const uniquePaths = (m, n) => {
    const dp = new Array(n).fill(1)
    for (let i = 1; i < m; i++) {
        for (let j = 1; j < n; j++) {
            dp[j] += dp[j - 1]
        }
    }
    return dp[j - 1]
}

总结

通过两个示例介绍了动态规划算法，其核心是分析相同问题（重叠子问题）找到状态转移方程，另外可以考虑优化一下空间复杂度，有好的想法欢迎大家留言分享，共同进步