Scrooge's Tower

Scrooge’s Tower

.
.
.
.
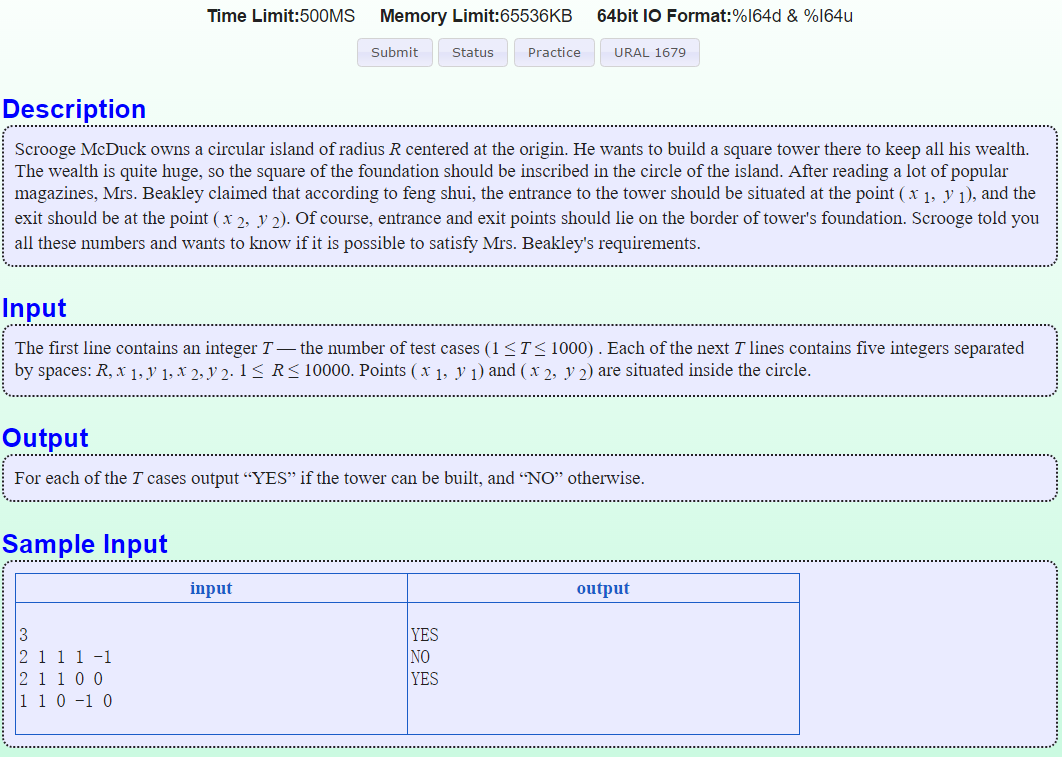
题意：园内有两个点，问这两个点是否出现在圆的内接正方形内
.
.
.
解法：一开始我们队想到通过旋转圆来看看两个点能否同时被转到内接圆上，因为内接正方形只设定一个。但是发现通过三角函数来旋转误差太大了，一直wa。然后改用直接计算内接正方形计算每个定点旋转后的相交点（4或8个），然后通过叉乘来判断两个向量的夹角是否和原来的相同，就过了。
.
.
.

#include <iostream>
#include <math.h>
#include <algorithm>
using namespace std;

int tt, n;
double r;
struct Node {
    double x, y;
}a, b;

double sqr(double x) {
    return x*x;
}

double len(Node& t) {
    return sqrt(sqr(t.x)+sqr(t.y));
}

double cheng(Node& t1, Node& t2) {
    return (t1.x*t2.y-t1.y*t2.x);
}

const int d[4][2] = {{1, 1}, {1, -1}, {-1, 1}, {-1, -1}};

int main() {
    cin >> tt;
    while (tt--) {
        cin >> r >> a.x >> a.y >> b.x >> b.y;
        if (len(a)-r/sqrt(2) < -1e-9 || len(b)-r/sqrt(2) < -1e-9) {
            cout << "NO" << endl;
            continue;
        }
        double t = cheng(a, b);
        Node temp1, temp2;
        temp1.y = r/sqrt(2);
        temp1.x = sqrt(sqr(len(a))-sqr(temp1.y));
        temp2.y = r/sqrt(2);
        temp2.x = sqrt(sqr(len(b))-sqr(temp2.y)); 

        bool flag = false;
        for (int i = 0; i < 4; i++)
            for (int j = 0; j < 4; j++) {
                temp1.x *= d[i][0];
                temp1.y *= d[i][1];
                temp2.x *= d[j][0];
                temp2.y *= d[j][1];
                if (fabs(cheng(temp1, temp2) - t) < 1e-5) flag = true;
                swap(temp1.x, temp1.y);
                if (fabs(cheng(temp1, temp2) - t) < 1e-5) flag = true;
                swap(temp2.x, temp2.y);
                if (fabs(cheng(temp1, temp2) - t) < 1e-5) flag = true;
                swap(temp1.x, temp1.y);
                if (fabs(cheng(temp1, temp2) - t) < 1e-5) flag = true;
                swap(temp2.x, temp2.y);
                temp1.x *= d[i][0];
                temp1.y *= d[i][1];
                temp2.x *= d[j][0];
                temp2.y *= d[j][1];             
            }

        if (flag) cout << "YES" << endl;
        else cout << "NO" << endl;
    }
}