逻辑回归的函数表达式为
用极大似然估计求解
每个样本发生的后验概率为
则所以样本发生总概率即似然函数为
L(θ)即为目标函数,-L(θ)即为loss函数,求-L(θ)最小
对数L(θ)函数为
对θ求导,即
无法求解。
用梯度下降法逼近最佳值,这里用的是梯度上升法,因为要求L(θ)最大值,其实道理一样。
整体梯度上升算法:
初始化wT=1
重复直至收敛:
计算整体梯度(∂l(θ)/∂θ)
根据θ+α*(∂l(θ)/∂θ)来更新回归系数wT
随机梯度上升算法:
初始化wT=1
重复直至收敛:
计算随机每个样本梯度(∂l(θ)/∂θ)
根据θ+α*(∂l(θ)/∂θ)来更新回归系数wT
逻辑回归的优点是实现简单,分类快。缺点是容易欠拟合,只能处理二分类问题(加上softmax优化可用于多分类),但是必须是线性可分的数据。
具体代码实现见我的github链接:https://github.com/AlanLin2015/Machine-Learning/tree/master/Logistics%20regressions








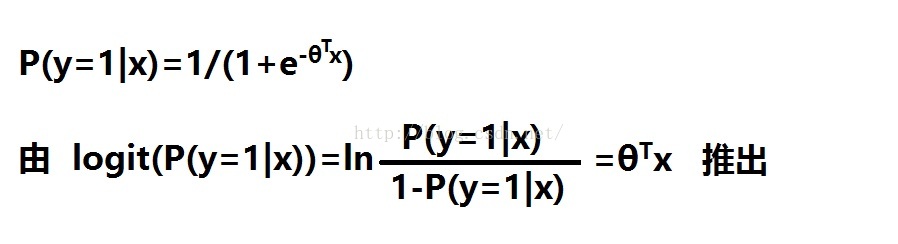
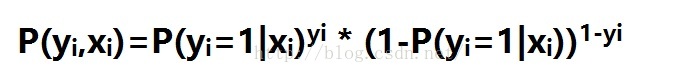

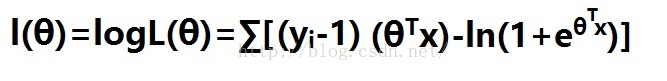
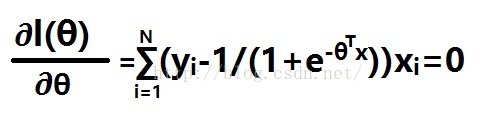
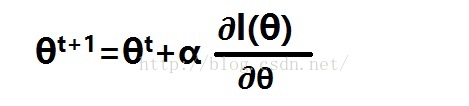














 1376
1376











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








