查找集合中两个最大的元素
启示:我们应该仔细检查证明过程中是否确实用到了所有的假设;应该设法用更少的假设完成同样的证明;另外,除非有反例说明已经到达所有可能的证明的边界,否则我们应该永不满足。
———Polyaand Szego[1927]
消除非实质性的假设有时能够得到更好的算法,不必要的假设有时意味着证明可能存在错误。
问题:已知集合S有n个元素x1,x2,….xn,求其中最大的和第二大的元素。
分析:我们要尽可能的减少比较次数,为简单起见,设n为2的幂。
分治:把S分成大小为n/2的两个子集P和Q。如果现在直接进行归纳,则假设已知P和Q中的最大和第二大的元素,分别记为p1,p2和q1,q2,然后查找S中的最大和第二大的元素。很明显,两次比较足以找到S中的这两个元素。第一次比较最大数p1和q1,此时得到一个新的第二大的数,这个数与原来的第二大的数(P或Q中的一个)比较一次,记为所求(比较过程见下图)。用这种方法得出递归关系T(2n)=2T(n)+2及T(2)=1,解得T(n)=3n/2-2。尽管这要优于直接进行的2n-3次比较,但算法还是可以在改进的。不是每一次找到的最大第二大元素都是有效的,只有到算法的最后我们才能确定最大元素和第二大元素。
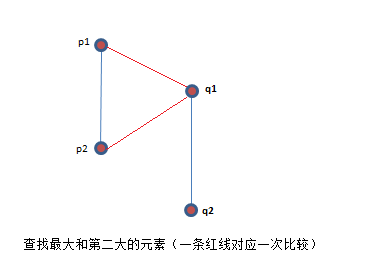
仔细分析上图的比较,可以看出算法不再使用q2,故q2的计算是多余的。如果能精简这样的计算,就可以进一步减少比较次数。然而,在p1和q1比较前,我们并不清楚p2和q2中的哪一个可以不必考虑,如果知道那个子集会“失败”,那么就可以在这个子集上用常规的查找最大数的算法了,这还能省去不少比较。看来我们已经意识到有些比较可以避免,只是不清楚究竟哪些可以忽略,那应该怎么做?
技巧:所以把第二大元素的计算推迟到算法的最后,只保留第二大元素的候选者列表。
归纳(第二次):给定一个小于n的集合,知道如何找到最大的元素以及第二大元素的一个“短短的”候选者列表。
短短的到底有多长尚未定义,但在算法设计过程中,我们会找到一个合适的值。
算法:给定大小为n的集合S,把它分为大小为n/2的字迹P和Q。由归纳假设可知两个集合最大的几个元素是p1和q1,在加上第二大元素的候选者集合Cp和Cq。首先比较p1和q1,取其中大者。例如p1作为S的最大数,然后舍去Cq,因为Cq中的所有元素都小于q1,接着再把q1加入Cp中。最终我们得到了一个最大的元素和一个候选者集合,从中可以直接选出第二大的数。查找最大数所需的比较次数满足递归关系T(n)=2T(n/2)+1及T(2)=1,解得T(n)=n-1。很容易看到,扩大一倍集合的大小时,我们能在候选者集合中再加入一个元素,所以lbn足以满足候选者集合大小的需要。于是查找第二大元素需要lbn-1次额外比较,因而总比较次数为n-1+lbn-1,恰为最可能的次数。n为2的幂时的归纳假设如下:
归纳(第三次):给定一个小于n的集合,知道如何求出最大的元素和第二大的元素的候选者集合,这个集合自多不超过lbn个元素。
参考代码:
vector<int>& get2max(int *arr,int len,int &max,vector<int> &candidate)
{
if(len == 1)
{
max = arr[len-1];
return candidate;
}
else if(len == 2)
{
if(arr[len-2] > arr[len-1])
{
max = arr[len-2];
candidate.push_back(arr[len-1]);
return candidate;
}
else
{
max = arr[len-1];
candidate.push_back(arr[len-2]);
return candidate;
}
}
int p1,q1;
vector<int> &candidate1 = *new vector<int>;
vector<int> &candidate2 = *new vector<int>;
//P子集中的候选者
candidate1 = get2max(arr,len/2,p1,candidate1);
//Q子集中候选者
candidate2 = get2max(arr+len/2,len - len/2,q1,candidate2);
if(p1 > q1)
{
max = p1;
candidate1.push_back(q1);
delete &candidate2;
return candidate1;
}
else if(p1 == q1)
{
max = p1;
candidate1.clear();
candidate2.clear();
candidate1.push_back(p1);
delete &candidate2;
return candidate1;
}
else
{
max = q1;
candidate2.push_back(p1);
delete &candidate1;
return candidate2;
}
}
void get2max(int *arr, int len)
{
int m1,m2;
vector<int> can;
can = get2max(arr,len,m1,can);
vector<int>::iterator i = can.begin();
m2 = can[0];
for(++i;i!=can.end(); ++i)
{
if(*i > m2)
m2 = *i;
}
cout<<"first maximum: "<<m1<<endl;
cout<<"second maximum: "<<m2<<endl;
}总结:如何改进一个算法,首先要看到这个算法的缺点,有时候在脑子里面运行一遍这个程序,缺点就暴露出来了。所以有必要检查是否存在对最终结果不起作用的部分,这些部分往往可以被删除,即使不能被删除,也可以用更简单、效率更高的运算代替。
分治算法会产生一些中间结果,并不是这些中间结果都对我们的最终结果有所帮助。






















 1743
1743

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








