深度学习第一课 第四周 深层神经网络用python的实现

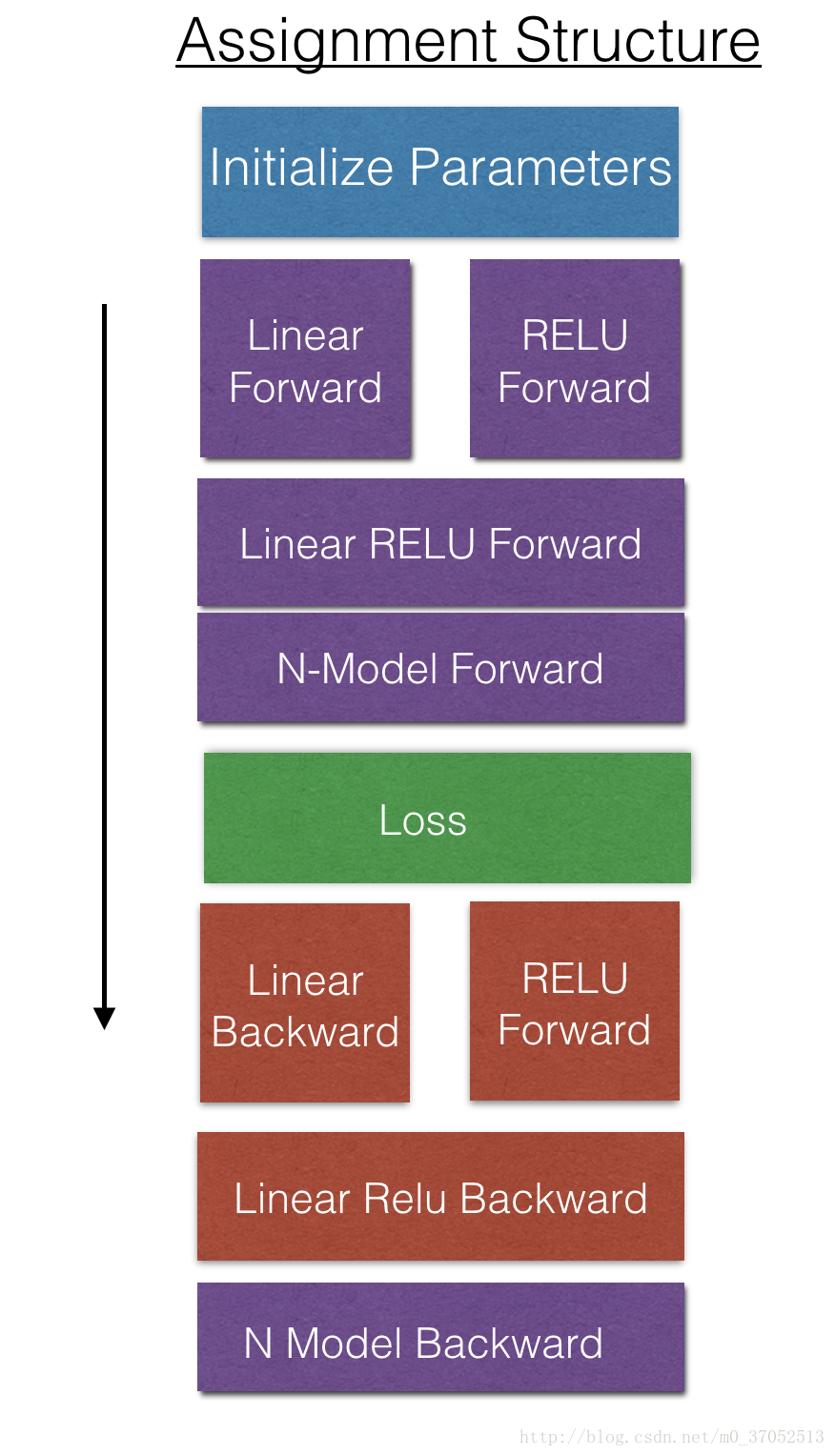
本文用吴恩达deeplearning.ai里的数据进行训练，相应的习题如下，写出一个n层的deeplearning程序，相应程序结构如图片所示：

相应代码实现如下：

import numpy as np
import matplotlib.pyplot as plt
import h5py
#%matplotlib inline

def load_data():
    x_train_set = h5py.File('datasets/train_catvnoncat.h5','r')
    x_train = np.array(x_train_set['train_set_x'][:])
    y_train = np.array(x_train_set['train_set_y'][:])
    x_test_set  = h5py.File('datasets/test_catvnoncat.h5','r')
    x_test  = np.array(x_test_set['test_set_x'][:])
    y_test  = np.array(x_test_set['test_set_y'][:])

    num_px  = x_train.shape[1]
    x_train = x_train.reshape(-1,num_px*num_px*3).T
    x_test  = x_train.reshape(-1,num_px*num_px*3).T
    y_train = y_train.reshape(1,-1)
    y_test  = y_test.reshape(1,-1)
    label_names = np.array(x_test_set['list_classes'][:])
    x_train = x_train / 255.0
    x_test  = x_test / 255.0
    return  x_train,x_test,y_train,y_test,label_names

x_train, x_test,y_train,y_test,label_names = load_data()
units_list = [x_train.shape[0],100,20,7,1]
activation_list = ['None','relu','relu','relu','sigmoid']
learning_rate = 0.0055

def sigmoid_forward(Z):
    '''
    sigmoid function do calc of z =1.0/(1+exp(-x))
    return  z
    '''
    A = 1.0/(1.0 + np.exp(-Z))
    assert(Z.shape == A.shape)

    return A

def sigmoid_backward(dA,Z):
    '''
    Inputs:
    dA: the backprop derivations of A
    Z:  in forwardprop A = g(Z)
    return:
    dZ: the gradient of Z
    '''
    temp_A = sigmoid_forward(Z)
    # dZ = dA*A(1-A)
    dZ = np.multiply(dA,np.multiply(temp_A,(1.0-temp_A)))
    assert(dA.shape == dZ.shape)
    return dZ

def relu_forward(Z):
    '''
    relu calc
    '''
    A = np.maximum(0,Z)
    assert(A.shape == Z.shape)
    return A

def relu_backward(dA,Z):
    '''
    relu backprop calc
    '''
    dZ = np.copy(dA)
    dZ[Z<0] = 0.0
    assert(dA.shape == dZ.shape)
    return dZ   

def init(X,units_list):
    '''
    function used to init variables about to use
    Inputs:
    X: inputs values used to train model
    units_list: list structure ,length is layer number, values represents units names(inputs as the 0 layers as first layers)
    Outputs:
    parameters : W,b  in every layers
    caches: Z,A  in every layers
    gradients : dZ,dA,dW,db in every layers
    '''
    np.random.seed(1)
    n_layers = len(units_list)
    m_samples = X.shape[1]
    parameters = []
    caches = []
    gradients = []
    for i in range(n_layers):
        param_temp = {}
        cache_temp = {}
        grad_temp  = {}
        if (i==0):
            param_temp['W'] = np.random.randn(units_list[i],units_list[i])*0.01  # will not used 
            param_temp['b'] = np.random.randn(units_list[i],1)*0.01              # will not used 
            cache_temp['Z'] = X                                                  # will not be used
            cache_temp['A'] = X                                                  #!!!!!!  trainning values important 
            grad_temp['dW'] = np.random.randn(units_list[i],units_list[i])*0.01  # will not used 
            grad_temp['db'] = np.random.randn(units_list[i])*0.01  # will not used 
            grad_temp['dA'] = np.random.randn(X.shape[0],X.shape[1])*0.01    # will not used 
            grad_temp['dZ'] = np.random.randn(X.shape[0],X.shape[1])*0.01    # will not used 
            parameters.append(param_temp)
            caches.append(cache_temp)
            gradients.append(grad_temp)
        else:
            param_temp['W'] = np.random.randn(units_list[i],units_list[i-1])*0.01
            param_temp['b'] = np.random.randn(units_list[i],1)*0.01
            cache_temp['Z'] = np.random.randn(units_list[i],m_samples)*0.01              
            cache_temp['A'] = np.random.randn(units_list[i],m_samples)*0.01
            grad_temp['dW'] = np.random.randn(units_list[i],units_list[i-1])*0.01
            grad_temp['db'] = np.random.randn(units_list[i],1)*0.01
            grad_temp['dA'] = np.random.randn(units_list[i],m_samples)*0.01
            grad_temp['dZ'] = np.random.randn(units_list[i],m_samples)*0.01
            parameters.append(param_temp)
            caches.append(cache_temp)
            gradients.append(grad_temp)
    return parameters, caches, gradients

# para,cach,grad = init(x_train,units_list)
# for i in range(len(units_list)):
    # print('out in:',i,'layers, w,b,, z,a, dw,db,dz,dz shapes')
    # print(para[i]['W'].shape,para[i]['b'].shape)  
    # print(cach[i]['Z'].shape,cach[i]['A'].shape)
    # print(grad[i]['dW'].shape,grad[i]['db'].shape,grad[i]['dA'].shape,grad[i]['dZ'].shape)

def linear_forward(X,W,b):
    '''
    calc the preocess w*x + b
    '''
    Z = np.dot(W,X) + b
    assert(Z.shape[0] == W.shape[0])
    assert(Z.shape[1] == X.shape[1])
    return Z

def linear_activation_forward(A_prev,W,b,activation='None'):
    '''
    function is a single layer calc
    return cache parameters
    outputs cache values of Z,A
    '''
    Z = linear_forward(A_prev,W,b)
    if(activation == 'relu'):
        A = relu_forward(Z)
    elif(activation == 'sigmoid'):
        A = sigmoid_forward(Z)
    else:
        A = Z
        print('wrong in activation function!!!')
    assert(Z.shape == A.shape)
    return Z,A

def n_layers_forward(parameters,caches,activation_list):
    '''
    this function calc the caches use w,b and Aprev
    '''
    n_layers = len(activation_list)
    for i in range(1,n_layers):
        A_prev = caches[i-1]['A']
        W = parameters[i]['W']
        b = parameters[i]['b']
        activation = activation_list[i]
        caches[i]['Z'], caches[i]['A'] = linear_activation_forward(A_prev,W,b,activation)
    return caches

def linear_backward(dZ,Aprev):
    '''
    single layers in linear calc backprop calc 
    Inputs:
    dZ: gradients of loss to ith layers' Z
    Aprev: cache values in (i-1) layers' matrix A
    Outputs:
    dW: gradients of loss to ith layers' W
    db: gradients of loss to ith layers' b
    '''
    m_samples = dZ.shape[1]
    dW = np.dot(dZ, Aprev.T)/np.float(m_samples)
    db = np.sum(dZ,axis=1,keepdims=True)/np.float(m_samples)

    return dW, db

def linear_activation_backward(Z,Aprev,Wplus,dZplus,activation):
    '''
    used to calc single layer's dZ,dA,dW,db
    Inputs:
    Z    : matrix of i th layers
    Aprev: matrix of previous layers
    Wplus: parameters of W of i+1 th layers
    dZplus: dz gradients of (i+1)th layers
    activation: activation function
    Outputs:
    dA: dA gradients of i th layers
    dZ: dZ gradients of i th layers
    dW: dW gradients of i th layers
    db: db gradients of i th layers
    '''
    dA = np.dot(Wplus.T,dZplus)
    if (activation == 'sigmoid'):
        dZ = sigmoid_backward(dA,Z)
    elif(activation == 'relu'):
        dZ = relu_backward(dA,Z)
    else:
        dZ = dA
        print('Wrong in calc dz,da,dw,db')
    dW,db = linear_backward(dZ,Aprev)

    return dZ,dA,dW,db

def n_layers_backward(Y,parameters,caches,gradients, activation_list):
    '''
    used to calc the n_layers gradients
    Inputs:
    parameters: w,b every layer model to learn
    caches:     Z,A every layers
    gradients:  used as inputs
    activation_list: every layers activation_function
    Outputs:
    gradients: cost function  gradients to every in dA,dZ,dW,db 
    '''
    n_layers = len(activation_list)
    for i in range(n_layers-1,0,-1):
        activation = activation_list[i]
        Z = caches[i]['Z']
        A = caches[i]['A']
        Aprev = caches[i-1]['A']
        if (i == n_layers -1):
            gradients[i]['dA'] = -np.divide(Y,A) + np.divide((1.0-Y),(1.0-A))
            dA = gradients[i]['dA']
            gradients[i]['dZ'] = sigmoid_backward(dA,Z)
            dZ = gradients[i]['dZ']
            gradients[i]['dW'],gradients[i]['db'] = linear_backward(dZ,Aprev)
        else:
            Wplus = parameters[i+1]['W']
            dZplus = gradients[i+1]['dZ']
            gradients[i]['dZ'],gradients[i]['dA'],gradients[i]['dW'],gradients[i]['db'] = \
            linear_activation_backward(Z,Aprev,Wplus,dZplus,activation)

    return gradients

def update_parameters(parameters,gradients,learning_rate):
    '''
    function used to update parameters w,b
    Inputs:
    parameters,gradients,learning_rate
    Outputs: 
    parameters: updated parameters
    '''
    n_layers = len(parameters)
    #print('shape of learning_rate',learning_rate)
    for i in range(1,n_layers):
        assert(parameters[i]['W'].shape == gradients[i]['dW'].shape)
        assert(parameters[i]['b'].shape == gradients[i]['db'].shape)
        parameters[i]['W']  += -learning_rate*gradients[i]['dW']
        parameters[i]['b']  += -learning_rate*gradients[i]['db']

    return parameters


def cost_function(AL,Y):
    '''
    function to calc cost values
    Inputs: AL last layers' cache matrix A
    Y: labeled samples targets
    Outputs:
    loss: total cost function values
    '''
    m_samples = Y.shape[1]
    AL.reshape(-1,1)
    Y.reshape(-1,1)
    loss = np.dot(Y.T,np.log(AL)) + np.dot((1.0-Y).T,np.log(1.0-AL))
    loss = -loss / np.float(m_samples)
    loss = loss.reshape(-1,1)
    loss = loss[0]
    return loss

def predict(AL,Y):
    '''
    function use learned parameters to predict 
    Inputs:
    AL: last layer cache matrix
    Y: labeled datas
    Outputs:
    accuracy: the predict accuracy real number
    '''
    AL = AL.reshape(-1,1)
    Y  = Y.reshape(-1,1)
    m_samples = Y.shape[0]
    counts = 0.0
    for i in range(m_samples):
        if AL[i] >=0.5:
            AL[i] = 1.0
        else:
            AL[i] = 0.0

    accuracy = np.sum(AL == Y)/np.float(m_samples)

    return accuracy

def learning_process(X,Y,units_list,activation_list,learning_rate = 0.0075):
    '''
    function used to learn model 
    Inputs:
    X: inputs data including features
    Y: labeled data
    learning_rate: learning_rate
    units_list :  layers length and layers units number
    activation_list: activations in each layer
    Outputs:
    parameters: learned W b in all layers
    loss: total cost function in convergence    
    '''
    n_layers = len(units_list)
    num_epoch = 200000
    loss_list = []
    accuracy_list = []
    steps = []
    plt.ion()
    plt.figure(1)
    plt.figure(2)
    loss_temp = 0.0
    parameters, caches, gradients = init(X,units_list)
    for i in range(num_epoch):
        caches = n_layers_forward(parameters,caches,activation_list)
        loss = cost_function(caches[n_layers-1]['A'],Y)
        dloss = np.abs(loss-loss_temp)/(np.abs(loss)+1.0e-15)
        loss_temp = loss
        gradients = n_layers_backward(Y,parameters,caches,gradients,activation_list)
        parameters = update_parameters(parameters,gradients,learning_rate)

        if(i%200 == 0):
            steps.append(i)
            loss_list.append(loss)
            accuracy_list.append(predict(caches[n_layers-1]['A'],Y))
            print('The trainning steps is {0} total loss is: {1} residual is:{2}'.format(i,loss,dloss))
            print('The trainning accuracy is {0}'.format(accuracy_list[-1]))
            plt.figure(1)
            line1,=plt.plot(steps,loss_list,'r',linewidth=1.5)
            plt.xlabel('Trainning steps')
            plt.ylabel('Total loss values')
            plt.legend([line1],['total loss'],loc = 'best')
            plt.figure(2)
            line2, = plt.plot(steps,accuracy_list,'g',linewidth=1.5)
            plt.xlabel('Trainning steps')
            plt.ylabel('Trainning Accuracy')
            plt.legend([line2],['Trainning Accuracy'],loc='best')
            plt.pause(0.01)

    return parameters, loss

parameters,loss = learning_process(x_train,y_train,units_list,activation_list,learning_rate)

print('final loss is:',loss)

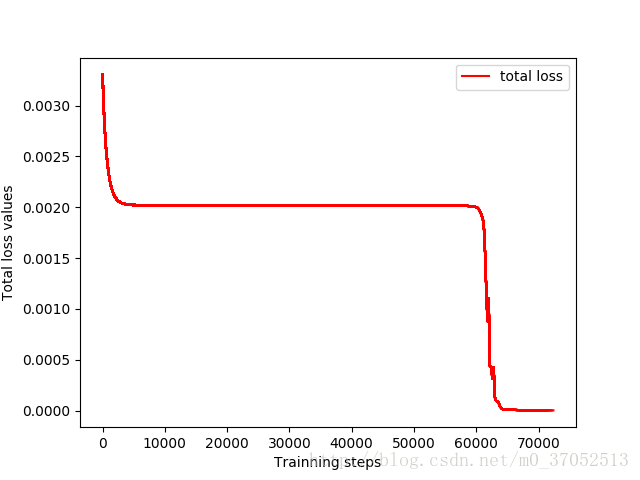
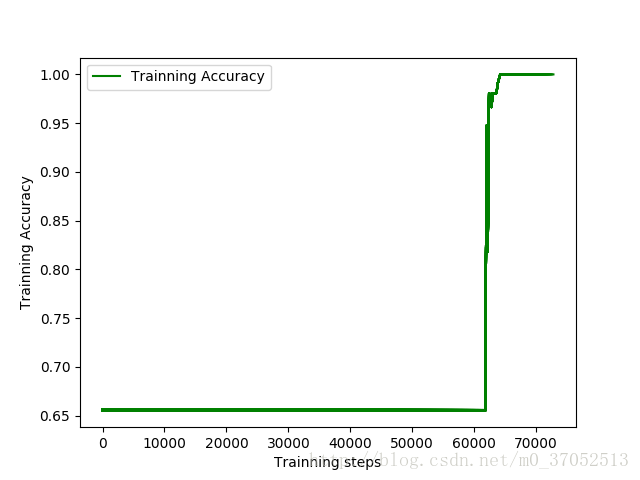
相应输出如下：