MATLAB中interp2参数使用指南

最新推荐文章于 2024-08-23 13:33:42 发布

执念斩长河

最新推荐文章于 2024-08-23 13:33:42 发布

阅读量2w

点赞数 19

分类专栏：数学建模文章标签： matlab 数学建模

本文链接：https://blog.csdn.net/m0_37149062/article/details/119455649

版权

数学建模专栏收录该内容

126 篇文章

订阅专栏

本文通过一个网格温度分布的例子，详细介绍了MATLAB中的interp2函数如何用于二维插值，使不光滑的曲面变得平滑。文章解释了interp2函数的参数用法，包括x0、y0、z0、x、y和不同的插值方法如nearest、linear、spline和cubic，并强调了参数的约束条件。通过实例展示了使用(interp2函数平滑曲面的效果，帮助读者理解并掌握该函数的使用技巧。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本文源于《数学建模》，interp2函数是matlab中的二维插值，下面用一个网格测量温度的例子讲解interp2函数如何使用吧。

一、例子：网格温度分布

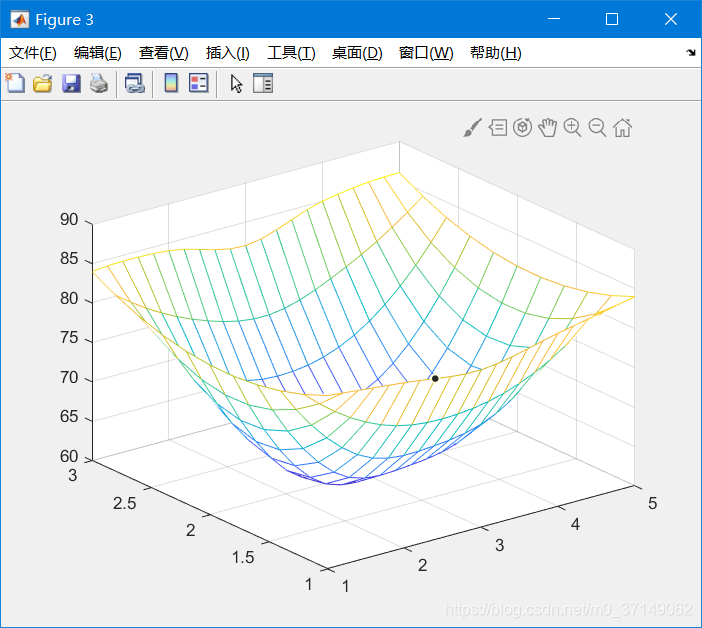
在这里插入图片描述
题目中分布曲面的图形画出来，效果是这样子的：

在这里插入图片描述

>> x=1:5;
>> y = 1:3;
>> temps = [82 81 80 82 84;79 63 61 65 81;84 84 82 85 86];
>> mesh(x,y,temps)

从图中可以看出，图形并不是光滑的。我们可以使用二维插值函数进行插值，将其图形变得光滑。那么二维插值函数如何使用呢？我们先使用(以0.2为单位进行作图)，再讲解
在这里插入图片描述

>> x=1:5;
>> y = 1:3;
>> temps = [82 81 80 82 84;79 63 61 65 81;84 84 82 85 86];
>> xi = 1:.2:5;
>> y1 = 1:.2:3;
>> zzi = interp2(x,y,temps,xi',y1,'cubic');
>> mesh(xi,y1,zi);