奇数阶幻方构造法

最新推荐文章于 2024-04-10 11:13:11 发布

Uniontake

最新推荐文章于 2024-04-10 11:13:11 发布

阅读量1.3w

点赞数 7

分类专栏：数论

数论专栏收录该内容

61 篇文章 1 订阅

订阅专栏

1.La Loubere 法奇数幻方构造

小时候玩幻方的时候没有去记这些口诀，每次我都会说我不喜欢记口诀，其实真正原因估计是懒，懒着懒着好像记性也变差了。(๑´ㅂ`๑)
老师带你们回顾一下 奇数阶幻方口诀的口诀—— 一居上行正中央，依次斜填切莫忘；上出框时向下放，右出框时向左放；排重便在下格填，右上排重一个样。这是由法国人 罗伯(do la loubere)总结出来的，所以都叫他罗（萝）伯（卜）法。（哈哈哈哈）

先解释一下这个口诀的意思：

一居上行正中央：数字 1 放在首行最中间的格子中；
依次斜填切莫忘：向右上角斜行，依次填入数字；
上出框时向下放：如果右上方向出了上边界，就以出框后的虚拟方格位置为基准，将数字竖直降落至底行对应的格子中；
右出框时向左放：同上，向右出了边界，就以出框后的虚拟方格位置为基准，将数字平移至最左列对应的格子中；
排重便在下格填：如果数字 $n$ 右上的格子已被其它数字占领，就将 $n+1$ 填写在 $n$ 下面的格子中；
右上排重一个样：如果朝右上角出界，和上面重复的情况做同样处理。

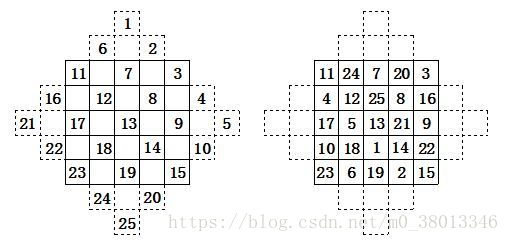
下面给出一个用这个方法构造的五阶幻方

但是这个方法，我只能回答到这里了，它的构造原理我暂时还不能很好的回答。
以前有看过幻方构造的出入相补原理法，可以解决2k+1,4k,4k+2阶的幻方构造，但是和罗伯法不一样，有兴趣的可以了解。

/**
    奇数幻方的构造:
    一居上行正中央：数字 1 放在首行最中间的格子中；依次斜填切莫忘：
    向右上角斜行，依次填入数字；
    上出框时向下放：如果右上方向出了上边界，就以出框后的虚拟方格位置为基准，将数字竖直降落至底行对应的格子中；
    右出框时向左放：同上，向右出了边界，就以出框后的虚拟方格位置为基准，将数字平移至最左列对应的格子中；
    排重便在下格填：如果数字右上的格子已被其它数字占领，就将 填写在下面的格子中；
    右上排重一个样：如果朝右上角出界，和上面重复的情况做同样处理。

    需要注意的是向上斜放
*/
#include<bits/stdc++.h>
using namespace std;
const int maxn = 100;
int maze[maxn][maxn];
void Huan(int n) {
    memset(maze,0,sizeof(maze));
    maze[0][n/2] = 1;

    int mx = n-1,my = n/2+1,it = 2;
    while(it <= n*n) {
        maze[mx][my] = it++;
        int tx = mx - 1;
        int ty = my + 1;
        if(tx < 0) {
            if(ty >= n) tx = tx + 2,ty = ty - 1;
            else tx = n-1;
        }
        else {
            if(ty >= n) ty = 0;
        }
        if(maze[tx][ty]) tx = mx + 1,ty = my;
        mx = tx;my = ty;
    }
}
int main()
{
    int n;
    while(~scanf("%d",&n))
    {
        Huan(n);

        for(int i=0;i<n;i++) {
            for(int j=0;j<n;j++) {
                printf("%d ",maze[i][j]);
            }
            printf("\n");
        }
    }
    return 0;
}

2.杨辉法

②
那我再来给大家讲讲另一种方法，这会是一种更为有趣的方法。这是我国古代数学家杨辉给出的一种巧妙的排法： 九子斜排，上下对易，左右相更，四维挺进。
举个例子：9个数斜着排，上下的两个数1,9，左右的两个数3,7互相换一下，四个角上的2,4,6,8就移到那四个角上去，这样就填好了一个三阶幻方了.

③
或许你会觉得这样子不是很漂亮，那就改进一下吧，斜排好九个数字后，就将上、下、左、右的四个数字向对方的方向（下、上、右、左）移动三格。那么这样就漂亮啦！这种方法就是巴舍法（平移补空法）啦~

个人觉得罗伯法简单易懂，只要会数数就够了，但是对于阶数比较大的幻方写起来会比较累，但是杨辉法和巴舍法对于解决阶数比较大的幻方会相对简单一些诶。

【讨论来了，biubiu~（觉得啰嗦的可以直接跳到最后看"魔力轮胎"~）

那么再来由另一种方法来借助坐标格点来代替格子，继续讨论三阶幻方构造的巴舍法到底是为什么可以这样做的。

如上图中的左图。
我们做第一步——九子斜排。

在点(0,2)处标记1，在点(1,1)处标记2，在点(2,0)处标记3，这是第一段；

在点(-1,1)，(0,0)，(1,-1)处分别标记4,5,6，这是第二段；

在点(-2,0)，(-1,-1)，(0,-2)处分别标记7,8,9，这是第二段；

那接下来第二步——画正方形。
以点(-1,1)，(1,1)，(1,-1)，(-1,-1)为顶点做一个正方形，我们发现1,9,3,7四个数在这个正方形外。
最后一步，吧位于正方形外的四个数，都向正方形内平移三个单位，就得到了三阶幻方（上图中的右图）。

为了讨论的方便，我们对于上述的三段，分别有如下记法：
第一段： $f_{1}(x,2-x) =x+a_{1}$ ，其中， $a_{1}=1,x=0,1,2$ ，也即：
$f_{1}(0,2) =1,f_{1}(1,1) =2,f_{1}(2,0) =1$ ;
第二段： $f_{2}(x,-x) =x+a_{2}$ ，其中， $a_{2}=5,x=-1,0,1$ ，也即：
$f_{2}(-1,1) =4,f_{2}(0,0) =5,f_{2}(1,-1) =6$ ;
第三段： $f_{3}(x,-2-x) =x+a_{3}$ ，其中， $a_{3}=9,x=-2,-1,0$ ，也即：
$f_{3}(-2,0) =7,f_{3}(-1,-1) =8,f_{3}(0,-2) =9$ .

这样，就建立好了一个函数列 $f_{i}(x,b_{i}-x ) =x+a_{i} ,i=1,2,3$
你也会发现这个函数列取决于两个等差数列：
$a_{1}=1, a_{2}=5,a_{3}=9,$ 其中公差 $d_{a} =4$ ；
$b_{1}=2, b_{2}=0,b_{3}=2,$ 其中公差 $d_{b} =-2$ ；
可以进行验算，发现三横行，三纵列，以及两条对角线的和，当然他们都等于15:，
这里给出主对角线和副对角线的验算：
主对角线： $4+5+6=f_{2}(-1,1)+ f_{2}(0,0)+f_{2}(1,-1)=(-1+5)+(0+5)+(1+5)=5+5+5=15$
副对角线：
$2+5+8=f_{1}(1,1)+ f_{2}(0,0)+f_{3}(-1,-1)=(1+1)+(0+5)+(-1+9)=1+5+9=15$
对于三横行和三纵行的算式都和副对角线一样，可以归结为 $a_{1}+ a_{2}+a_{3}=1+5+9=15$ ，数列各项的和就是幻和。

（更多详细的验证可以见奇数阶幻方的杨辉方法，这是我以前发现的一个还可以的证法，相对初等好理解）
对于三阶幻方，我们发现数列 $a_{1}, a_{2},a_{3}$ 的公差为1 $1,2,\cdot \cdot \cdot ,n^{2}$ +3=4，
对于五阶幻方，同理可以发现 $a_{1}, a_{2},a_{3},a_{4},a_{5}$ 公差为1+5=6
……
嗯，就是对于幻方的幻和 $\frac{n+n^{3} }{2}$ ，其实就是 $1,2,\cdot \cdot \cdot ,n^{2}$ 中最中间的 $n$ 个数的和.
比如对于1,2,……4就是2+3=5
比如对于1,2,……9就是4+5+6=15
比如对于1,2,……25就是11+12+……+15=65
这个结论是正确的，证明交给你们去吧……（我不该这样的）

好了，对于任意的奇数阶方阵，我们就有如下的构造方法：

①将 $1,2,\cdot \cdot \cdot ,n^{2}$ 排成一个斜的 $n\times n$ 方阵；
②以 $\frac{n^{2}+1 }{2}$ 为中心做一个 $n\times n$ 方阵（格）；
③将位于这个 $n\times n$ 方阵（格）外的所有元素都向方阵内平移 $n$ 格。
好了这样就填好了一个奇数阶的幻方！=￣ω￣=

举个例子： $n=5$

继续利用我们在三阶幻方中构造的函数来看， $f_{i}(x,y)=x+a_{i}$ ，就是对于每个点的横坐标加上常数 $a_{i}$ ，而这个 $a_{i}$ 是一个等差数列，首项为1，公差为 $n+1$ .

偶阶幻方
当n为偶数时，我们称幻方为偶阶幻方。当n可以被4整除时，我们称该偶阶幻方为双偶幻方；当n不可被4整除时，我们称该偶阶幻方为单偶幻方。

先看看4阶幻方的填法：将数字从左到右、从上到下按顺序填写：

1       2       3       4
5       6       7       8
9      10     11     12

13 14 15 16

将对角线上的数字，换成与它互补的数字。
这里，n*n+1 = 4*4+1 = 17；
把1换成17-1 = 16；把6换成17-6 = 11；把11换成17-11 = 6……换完后就是一个四阶幻方。

对于n=4k阶幻方，我们先把数字按顺序填写。写好后，按4*4把它划分成k*k个方阵。因为n是4的倍数，一定能用4*4的小方阵分割。然后把每个小方阵的对角线，象制作4阶幻方的方法一样，对角线上的数字换成（整个大矩阵的）互补的数字，就构成幻方。

下面是8阶幻方的作法：
(1) 先把数字按顺序填。然后，按4*4把它分割成2*2个小方阵

(2) 每个小方阵对角线上的数字，换成和它互补的数。

链接：https://www.zhihu.com/question/30498489/answer/49208033
来源：知乎

Uniontake

关注

7
点赞
踩
41

收藏

觉得还不错? 一键收藏
0
评论
奇数阶幻方构造法

1.La Loubere 法奇数幻方构造小时候玩幻方的时候没有去记这些口诀，每次我都会说我不喜欢记口诀，其实真正原因估计是懒，懒着懒着好像记性也变差了。(๑´ㅂ`๑)老师带你们回顾一下奇数阶幻方口诀的口诀——一居上行正中央，依次斜填切莫忘；上出框时向下放，右出框时向左放；排重便在下格填，右上排重一个样。这是由法国人罗伯(do la loubere)总结出来的，所以都叫他罗（萝）伯（卜）法。（哈哈哈...
复制链接

扫一扫