【论文阅读】A survey of the use of iterative reconstruction algorithms in electron micrography

注：下文只总结文章中关于cryoET重建的部分。

题目

迭代重建法在电子显微镜中的应用综述

摘要

电子显微镜的关键步骤之一是根据显微镜获取的一组二维 (2D) 投影对所研究样本的三维 (3D) 图进行断层扫描重建。可以使用不同的重建算法执行断层扫描重建，这些算法可分为几大类：直接傅里叶反演方法、反投影方法、Radon 方法或迭代算法。在本篇综述中，我们将重点介绍迭代算法，解释该类算法在电子显微镜领域引入的不同算法背后的数学原理。我们将介绍它们在单粒子分析 (SPA) 和电子断层扫描 (ET) 中的应用。

简介

电子断层扫描 (ET) 中的情况通常特别复杂，因为投影图像数量较少、存在缺失楔形以及图像非常大，对计算资源构成了重大挑战（尤其是在内存方面；有关单粒子分析和电子断层扫描之间的比较，请参阅 Jonic 等人。[47]）。试图减少重建伪影和执行时间的 3D 重建算法的研究相当激烈，尤其是在最近十年 [48-61]。类似地，ET 中的纯重建算法可以与先验信息相结合，结合重建在某些领域是稀疏的这一事实或利用被成像对象的离散性质 [62-76]。

在本篇综述中，我们重点关注迭代重建算法系列，也称为级数展开法。经典算法（ART、Block ART 和 SIRT）之后出现了许多更现代的算法，如共轭梯度法、次梯度下降法、投影次梯度法、优越化法、ADMM 等，允许各种正则化，特别强调稀疏性促进正则化器。我们首先展示如何将 3D 重建问题视为求解线性方程组的问题。然后，我们将更经典的方法放在一个通用的代数框架中。最后，我们介绍了更现代的方法背后的原理。

三维重建作为方程组问题

电子显微镜收集的图像可以理解为被成像大分子库仑势的平行投影。三维模型
$V(\tilde{r}):{\mathbb{R}}^3\times 1\to \mathbb{R}$ 与投影图像 $I(\tilde{s}):{\mathbb{R}}^2\times 1\to \mathbb{R}$ 之间的关系由以下公式给出 [77]

$$I_{\tilde{A}}(\tilde{s})={\int }_{-\infty }^{\infty }V({\tilde{A}}^{-1}{\tilde{H}}^T\tilde{s})dt$$

这里 $\tilde{r}=(x,y,z,1)$，$\tilde{s}=(x,y,1)$ 分别是3D点和2D点的齐次坐标。t是积分变量。

${\tilde{H}}^T$是：

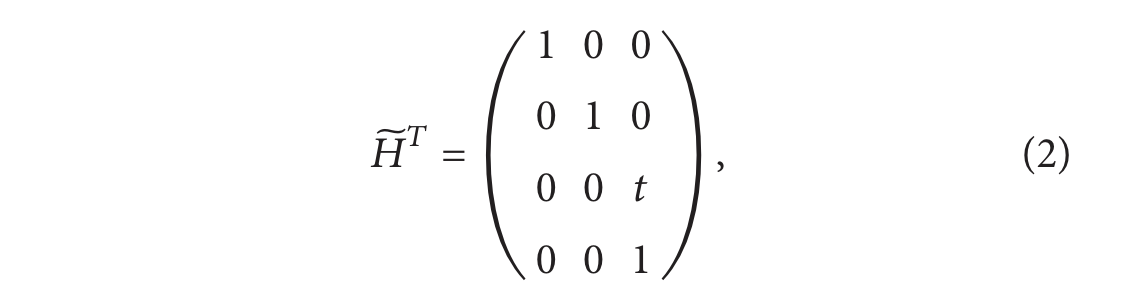
$\tilde{A}$ 是指定投影的视点的矩阵（R 是旋转矩阵，通常由3个欧拉角指定，t是平面内位移）。每个投影都有自己的矩阵A，反应每个图像的不同投影方向和单独的偏移。实际上这种理想图像不会出现，会被随机噪声破坏（其性质和大分子周围的并结构以及电子束的随机到达有关），并且投影图像旨在一组离散位置上（投影图像像素中心点）已知。

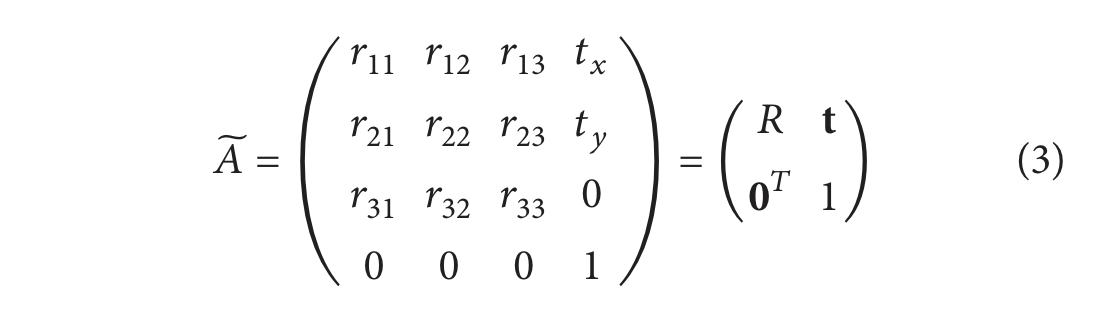
于是方程可以写成：

$$I_{\tilde{A},i}=I_{\tilde{A}}({\tilde{s}}_i)={\int }_{-\infty }^{\infty }V({\tilde{A}}^{-1}{\tilde{H}}^T{\tilde{s}}_i)dt+n_i$$

注意这里使用加性噪声，且噪声具有高斯分布。现在假设我们将体积表示为函数的线性组合$b(\tilde{r})$，移到一组已知位置 ${\tilde{r}}_j$（通常这些位置规则地分布在网格上）：

$$V(\tilde{r})=\sum _j{x}_{j}b(\tilde{r}-{\tilde{r}}_j)$$
基函数可以是体素，也可以是任何其他从断层扫描角度来看具有一些有趣特性的函数（比如 Kaiser-Bessel 修正函数，也称为blob，[32,36]可以降低三维重建中的噪声）。

断层扫描问题的目标是确定基础系数$x_j$，使得实验投影实际上是体积$V$的线性积分。将上式带入之前的公式，先忽略噪声项，可以得到方程（6）：

$$I_{\tilde{A},i}={\int }_{-\infty }^{\infty }V({\tilde{A}}^{-1}{\tilde{H}}^T{\tilde{s}}_i)dt$$
$$={\int }_{-\infty }^{\infty }(\sum _j{x}_{j}b({\tilde{A}}^{-1}{\tilde{H}}^T{\tilde{s}}_i-{\tilde{r}}_j)dt$$
$$=\sum _j{x}_j({\int }_{-\infty }^{\infty }b({\tilde{A}}^{-1}{\tilde{H}}^T{\tilde{s}}_i-{\tilde{r}}_j)dt)=\sum _j{x}_j{a}_{\tilde{A},ij}$$

其中 $a_{\tilde{A},ij}$ 是位于 ${\tilde{r}}_j$ 处、位置 ${\tilde{s}}_i$ 处的基函数沿几何变换 𝐴̃ 确定的方向的线性积分，即体积的第 𝑗 个基函数对图像中第 𝑖 个像素的贡献。我们可以使用字典顺序将图像像素写成单个向量，并且可以将上述方程重写为矩阵形式：

$$I_{\tilde{A}}=A_{\tilde{A}}\mathbf{x}$$

如果我们有 $P\times P$ 像素大小的图像，假设重建体积为 $B\times B\times B$ 的立方体，然后 $I_{\tilde{A}}\in {\mathbb{R}}^{P^2}$ 是一个$P^2$维的向量，$\mathbf{x}\in {\mathbb{R}}^{B^3}$ 维度的向量，而 $A_{\tilde{A}}$ 是一个大小为 $P^2\times B^3$ 的矩阵。如果从像素层面去考虑，可以写成：

$$I_{\tilde{A},i}=a_{\tilde{A},i}^T\mathbf{x}=⟨a_{\tilde{A},i},\mathbf{x}⟩$$

其中 $a_{\tilde{A},i}^T$ 是矩阵的第 $i$ 行。这是${\mathbb{R}}^{{\mathbb{B}}^3}$空间中超平面的方程，这意味着投影图像的每个像素都为定位体积系数 $\mathbf{x}$ 提供了超平面约束。在理想的无噪声情况下，真实的 $\mathbf{x}$ 必须位于所有像素定义的所有超平面的交点处（测量值观察到的噪声只是随机地沿垂直于超平面法线的方向移动每个超平面)。这样，单个投影提供了 $P^2$ 个方程，但是我们有 $B^3$ 个未知数。因此有无数个结构和单个投影兼容。在电子显微镜中，我们收集了数千张投影图像（假设为M），并且我们可能会将所有测量值堆叠在一个大向量中。相应的方程组将是：

$$\left(\begin{array}{c}{\mathbf{I}}_{{\tilde{A}}_1}\\ {\mathbf{I}}_{{\tilde{A}}_2}\\ ⋮\\ {\mathbf{I}}_{{\tilde{A}}_M}\end{array}\right)=\left(\begin{array}{c}{A}_{{\tilde{A}}_1}\\ A_{{\tilde{A}}_2}\\ ⋮\\ A_{{\tilde{A}}_M}\end{array}\right)\mathbf{x}$$

可以写成线性方程组：
$$\mathbf{b}=A\mathbf{x}$$

这里 $\mathbf{b}\in {\mathbb{R}}^{M{P}^2}$ 是一个包含了所有实验投影图像的向量，A是一个包含了所有投影矩阵的矩阵，大小为 $M{P}^2\times B^3$。这个矩阵非常稀疏，对于常见的基函数（如体素、斑点等），体积中只有少数系数对每个像素有贡献（只有沿着通过该像素的积分线的系数）。给出EM中的一些典型示例，比如我们有 M=50000 张大小为 $P\times P=256\times 256$ 的图像。将有 $M{P}^2=33$亿个方程和 $B^3=P^3=1680$ 万个未知数（如果用体素作为基函数）。由于测量噪声，方程组不一致，必须寻求某种最小二乘解。

我们仅针对数据收集集合结构介绍了线性方程组。但是，可以轻松结合显微镜的对比度传递函数（CTF）（即显微镜如何模糊理想图像）。卷积可以通过使用 Toeplitz 矩阵的矩阵乘法来表示，这样可以使用矩阵 $C{A}_{\tilde{A}}$ 来代替包含纯集合信息的 $A_{\tilde{A}}$ 矩阵，其中 C 是CTF Toeplitz 矩阵（每个实验图像可能都有自己的CTF矩阵）。

有趣的是，将断层扫描问题视为线性方程组也可以在傅里叶空间中完成，得益于中心切片定理，大分子模型的三维傅里叶变换和投影的二维傅里叶变换之间的关系可以表示为：

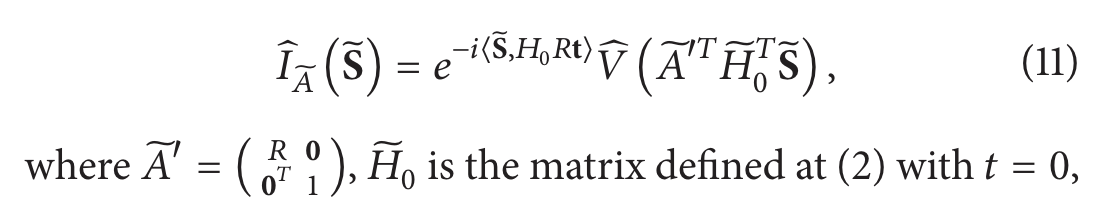
并且 $H_0$ 除了最后一行（添加其齐次性质的行）外和 ${\tilde{H}}_0$ 是相同的矩阵。$\tilde{S}$ 是二维频率坐标，${\hat{I}}_{\tilde{A}}$ 和 $\hat{V}$分别是投影图像和大分子模型的2D和3D傅里叶变换。要计算2D频率坐标 $\hat{S}$ 处的傅里叶系数，需要计算坐标 ${\tilde{A}}^{\prime T}{\tilde{H}}_0^T\tilde{S}$ 处体积的傅里叶变换，然后乘上对应的相位项e，以解释图像中的偏移。实际上，我们没有在任意位置上体积的傅里叶变换，必须从其周围的3D傅里叶系数中插值得到。让我们关注频率 ${\tilde{S}}_j$ 并将相应的二维傅里叶系数称为$I_j$，用 ${\tilde{V}}_j$ 来表示第 $j$ 个3D傅里叶系数。然后，可以将二维傅里叶系数插值如下：

$${\hat{I}}_i=\sum _j{\hat{V}}_j{\hat{a}}_{\tilde{A},ij}$$

其中 ${\hat{a}}_{\tilde{A},ij}$ 包括相移和插值权重。该方程在形式上和（6）相同，意味着傅里叶空间中的3D重建问题也可以表示为线性方程组，而且要小心执行插值。事实上，在这里包含CTF基比在真实空间更容易，因为只需要将 ${\hat{a}}_{\tilde{A},ij}$ 乘以CTF系数 $c_i$即可。

（加权）最小二乘解

对于不一致的方程组 $A\mathbf{x}=\mathbf{b}$，我们可以尝试寻找一个 $\mathbf{x}$，使其到由实验测量的像素值给出的所有超平面的距离最小化。通过最小化残差向量 $A\mathbf{x}-\mathbf{b}$ 的范数来实现这一点。在断层成像术语中，$A\mathbf{x}$ 可以解释为给定大分子模型 $\mathbf{x}$ 的预期实验投影，而 $\mathbf{b}$ 是实验测量的投影。我们的目的是找到模型 $\mathbf{x}$，使得它的重投影与实验获取的图像尽可能相似。实验图像与重投影之间比较的残差应仅为实验图像中存在的噪声。

$$\mathbf{x}=argmi{n}_{\mathbf{x}}\Vert A\mathbf{x}-{b\Vert }^2$$

其中范数是使用标准内积计算的。这是一个线性最小二乘问题。解决方案不是唯一的（矩阵$A$ 的核中的任意向量 ${\mathbf{x}}_0$都会产生相同的误差范数，因为 $A(\mathbf{x}+{\mathbf{x}}_0)=A\mathbf{x}+0=A\mathbf{x}$。实际上，${\mathbf{x}}_0$ 指的是傅里叶系数位于实验图像未测量的区域中的任何结构。在优化问题中对于范数可以写成：

$$\mathbf{x}=argmi{n}_{\mathbf{x}}(A\mathbf{x}-\mathbf{b}{)}^T(A\mathbf{x}-\mathbf{b})$$
$$=argmi{n}_{\mathbf{x}}\Vert b{\Vert }^2+{\mathbf{x}}^T{A}^{T}A\mathbf{x}-2{\mathbf{x}}^T{A}^T\mathbf{b}$$
微分并等于0，得到：
$$A^{T}A\mathbf{x}=A^T\mathbf{b}$$

这是最小二乘问题的正态方程，可以证明任何正态方程的解也是最小二乘问题的解，反之亦然。除了退化情况外，$A^{T}A$ 是一个正定矩阵，这意味着矩阵可逆，因此正态方程有唯一解。对于复数，范数定义为：

$$\Vert \mathbf{u}{\Vert }^2={\mathbf{u}}^H\mathbf{u}$$

其中 $H$ 为共轭转置，因此傅里叶空间中的正则方程为：
$$A^{H}A\mathbf{x}=A^H\mathbf{b}$$

如果有些测量值比其他测量值更可靠，那可以在最小化中引入权重（在实空间中这更难，但在傅里叶空间中低频分量相对于高频分类而言过多，因此它们的权重降低）。给定一个对角正定矩阵 $W$，大小是 $M{P}^2\times M{P}^2$，我们可以定义 $W$ 内积为：
$$⟨\mathbf{u},\mathbf{v}{⟩}_W={\mathbf{u}}^{H}W\mathbf{v}$$
$$A^{H}WA\mathbf{x}=A^{H}W\mathbf{b}$$
解决该方程组的最直接方法是使用 Moore-Penrose 伪逆：
$$\mathbf{x}=(A^{H}WA{)}^{-1}{A}^{H}W\mathbf{b}=A^{†}b$$

矩阵 $A^{H}WA$ 的尺寸是 $B^3\times B^3$，它的直接求逆通常超过了现有计算机的能力。通常使用避免求逆此矩阵的数值算法。下节会讲到。

线性方程组的迭代解

上面的方程组的形式大致都为：
$$\mathcal{A}\mathbf{x}=b$$

在本节中，$\mathcal{A}$ 和 $b$ 都是通用的矩阵和数据项，和它们在显微投影图像、CTF、傅里叶或实空间版本等方面的实际表达无关。

一种简单但通用的方法来生成求解上式的迭代算法，就是将矩阵 $\mathcal{A}$ 分解成另外两个矩阵$\mathcal{M}$和 $\mathcal{N}$ 的差，如下:
$$\mathcal{A}=\mathcal{M}-\mathcal{N}$$
于是：
$$(\mathcal{M}-\mathcal{N})\mathbf{x}=b$$

$$\mathcal{M}{\mathbf{x}}^{(k+1)}=\mathcal{N}{\mathbf{x}}^{(k)}+b$$

$${\mathbf{x}}^{(k+1)}={\mathcal{M}}^{-1}\mathcal{N}{\mathbf{x}}^{(k)}+{\mathcal{M}}^{-1}b$$
$$={\mathbf{x}}^{(k)}+{\mathcal{M}}^{-1}(b-\mathcal{A}{\mathbf{x}}^{(k)})$$

这种迭代方案具有有趣的特性，如果残差为 $b-\mathcal{A}{\mathbf{x}}^{(k)}=0$ 即成功找到了方程组的解，当前解无需更新。

1. Jacobi. $\mathcal{A}$ 分解成其对角矩阵 $\mathcal{D}$ 和两个下三角矩阵 $\mathcal{L}$ 和上三角矩阵 $\mathcal{U}$：
   $$\mathcal{A}=\mathcal{D}-(\mathcal{L}+\mathcal{U})$$
   $${\mathbf{x}}^{(k+1)}={\mathbf{x}}^{(k)}+{\mathcal{D}}^{-1}(b-\mathcal{A}{\mathbf{x}}^{(k)})$$

2. Gauss-Seidel. $\mathcal{A}$ 和上面进行相同的分解，但是矩阵用法不同：
   $$\mathcal{A}=(\mathcal{L}+\mathcal{D})-\mathcal{U}$$
   $${\mathbf{x}}^{(k+1)}={\mathbf{x}}^{(k)}+(\mathcal{L}+\mathcal{D}{)}^{-1}(\mathcal{C}-\mathcal{A}{\mathbf{x}}^{(k)})$$

3. Richardson. 使用单位矩阵作为参考来分解 $\mathcal{A}$：
   $$\mathcal{A}=I-(I-\mathcal{A})$$

$${\mathbf{x}}^{(k+1)}={\mathbf{x}}^{(k)}+(\mathcal{C}-\mathcal{A}{\mathbf{x}}^{(k)})$$

这些数值方案成功解决方程组 $\mathcal{A}\mathbf{x}=b$ 的原因在此方法里可以很好地说明。迭代算法可以写为：
$${\mathbf{x}}^{(k+1)}=b+(I-\mathcal{A}){\mathbf{x}}^{(k)}$$

从 ${\mathbf{x}}^{(0)}=0$ 开始，对 $\mathbf{x}$ 的估计为：
$${\mathbf{x}}^{(1)}=\mathcal{C}$$
$${\mathbf{x}}^{(2)}=\mathcal{C}+(I-\mathcal{A})\mathcal{C}$$
$${\mathbf{x}}^{(3)}=\mathcal{C}+(I-\mathcal{A})\mathcal{C}+(I-\mathcal{A}{)}^2\mathcal{C}$$
$$⋮$$
$${\mathbf{x}}^{(k)}=\left(\sum _{m=0}^{k-1}(I-\mathcal{A}{)}^m\right)\mathcal{C}$$

如果 $\mathcal{A}$ 是可逆矩阵，则 ${\sum }_{m=0}^{\infty }(I-\mathcal{A}{)}^m$ 收敛于 ${\mathcal{A}}^{-1}$，只要对矩阵A 的所有特征值 ${\lambda }_i$ 满足 $0<|1-{\lambda }_i|<1$，对实特征值转化为$0<{\lambda }_i<2$ [82, Section 3.5.1]。实际上，这类迭代算法通常被修改为引入松弛因子${\mu }_k$(每次迭代可能不同):

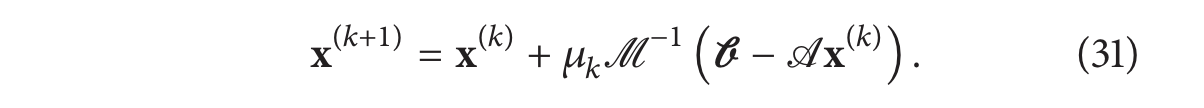
该松弛因子有助于通过修改参与收敛分析的矩阵的特征值来增加算法的收敛半径（我们已经看到了 Richardson 迭代的分析，但其余方案需要不同的矩阵）。有研究根据数字序列 ${\mu }_k$ 的性质分析重建算法的收敛性 [83]。SIRT 是电子断层扫描中最流行的重建算法之一。如下所示，SIRT 是将雅可比算法应用于具有特定加权方案的法方程的结果。让我们考虑实空间中加权最小二乘问题的法方程：

$$A^{H}WA\mathbf{x}=A^{H}W\mathbf{b}$$
具有松弛参数的雅克比更新为：

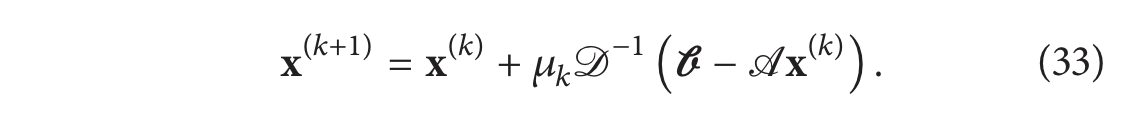
让我们将矩阵 𝐴 分解到不同的行（记住第 𝑖 行表示体积中的每个基函数对第 𝑖 个像素的贡献）和列（第 𝑗 列表示第 𝑗 个基函数如何影响测量中的所有像素）中，

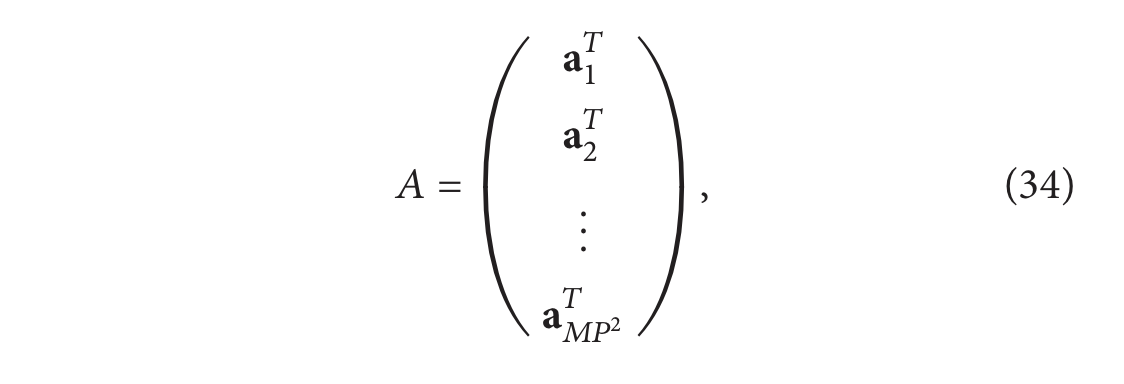
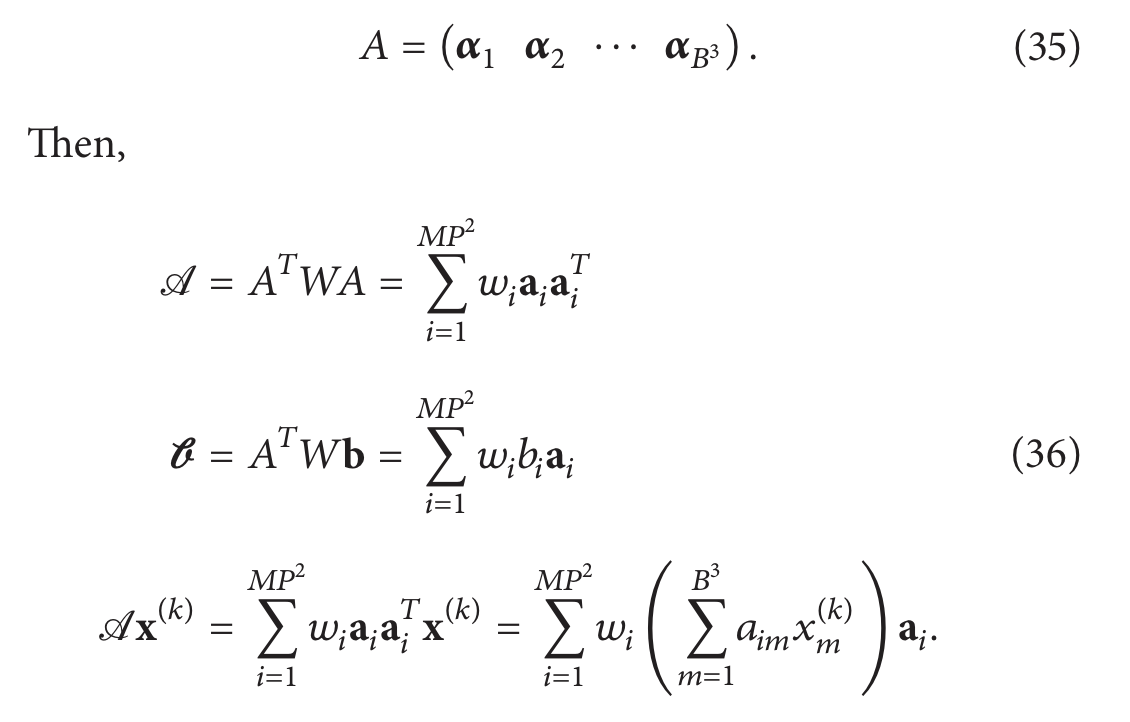
现在看给定的基函数j:

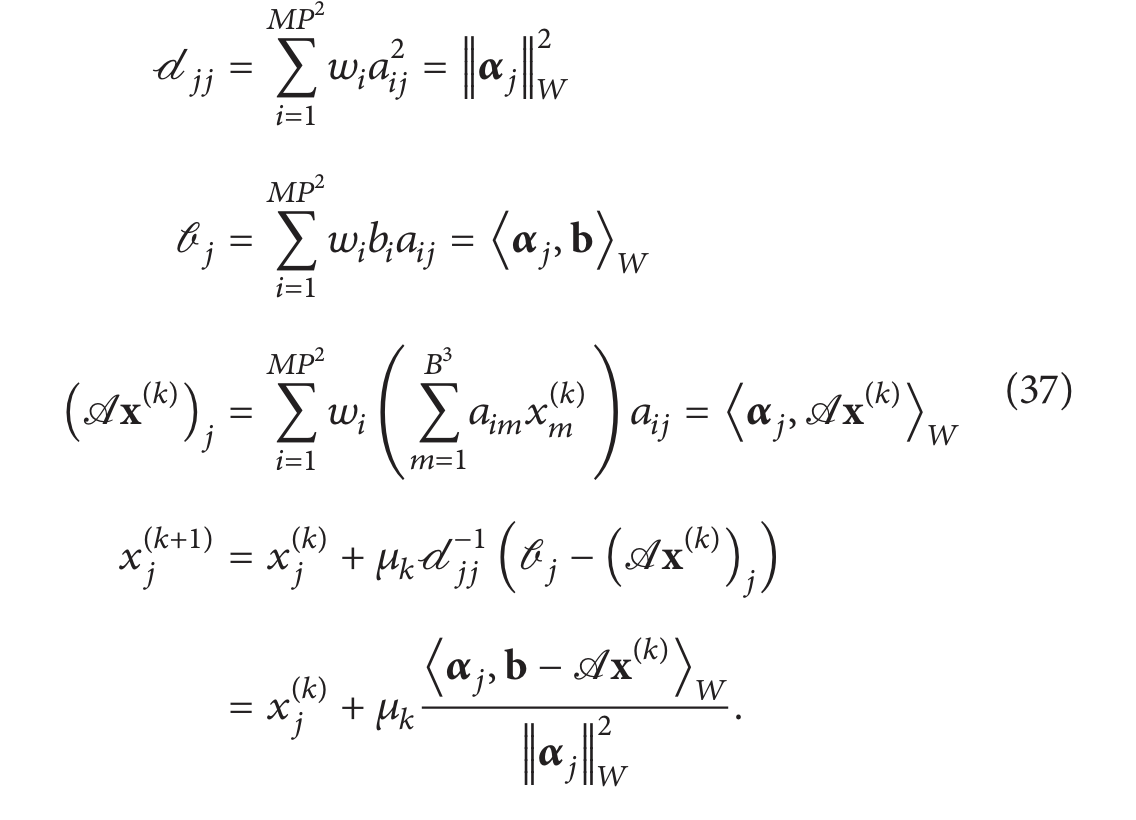
有趣的是，如果当前图像残差 $(b-A{x}^{(k)})$ 与 ${\alpha }_j$ 𝑊 正交，即改变第 𝑗 个基函数的系数不会影响残差，那么，正如预期的那样，第 𝑗 个基函数的系数不会改变。

在EM中习惯将 SIRT 表示为：

下面，我们来证明这两个公式（(37) 和 (38)）并不等价。实际上，SIRT 并不是一个单一的算法，而是一个完整的重建算法系列 [84]；每个算法都提供了对重建过程的不同见解。如果我们看 (38) 中的特定基函数 𝑗，我们有

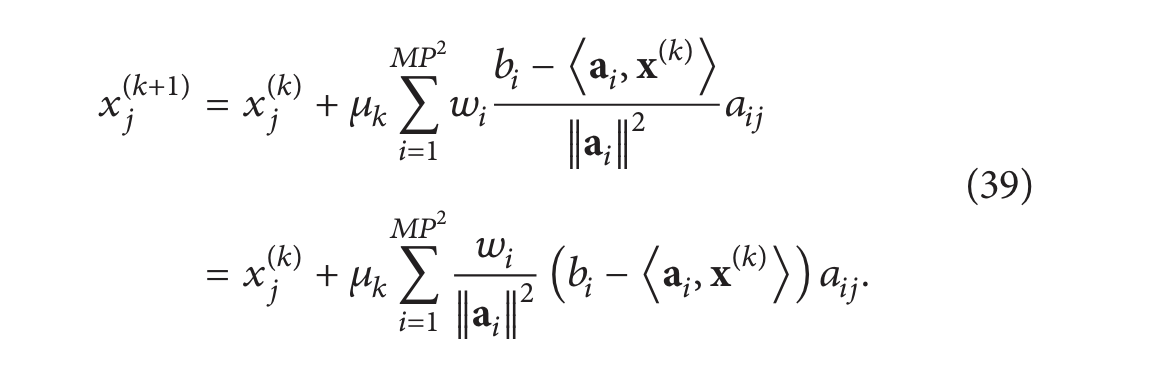
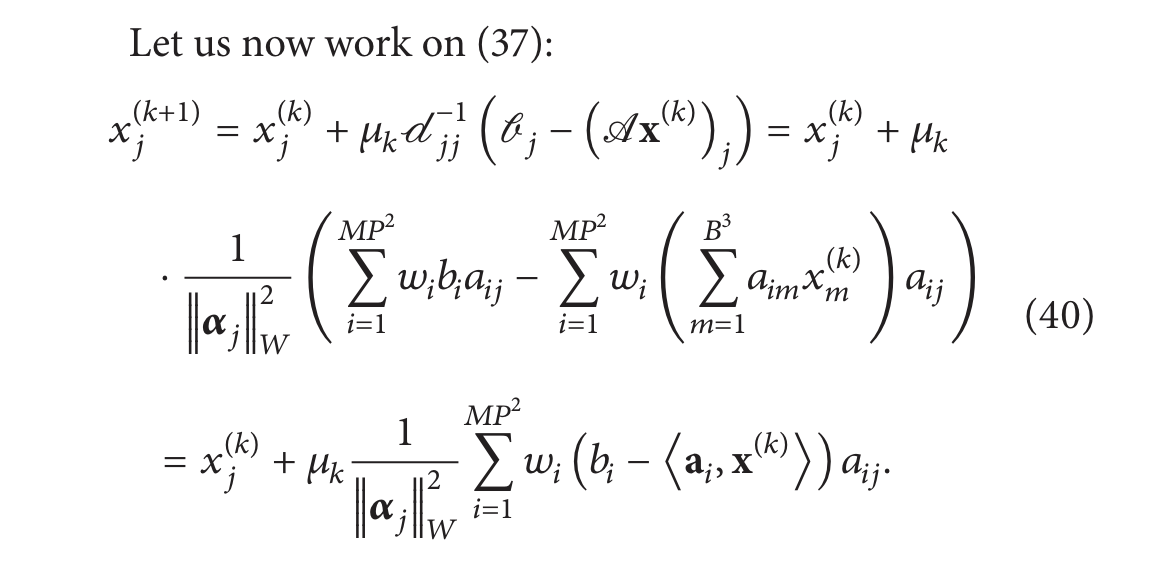
(39) 和 (40) 中的算法明显不同，但是它们都被称为 SIRT，并且都属于 SIRT
算法系列。任何形式为

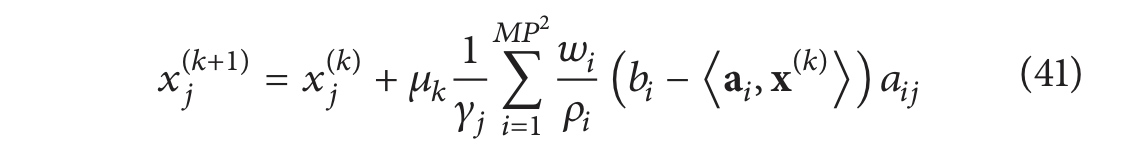
对于合适的𝛾 和 𝜌的算法也被认为是 SIRT算法 [84]。一个特定的类已经证明是收敛的 [84] 是
$${\gamma }_j=\sum _{i=1}^{M{P}^2}{w}_i|a_{ij}{|}^{\alpha }$$
$${\rho }_i=\sum _{j=1}^{B^3}|a_{ij}{|}^{2-\alpha }$$
$$0<\alpha \le 2,0<{\mu }_k<2.$$

雅克比迭代（方程40）得出的结果对应于 $\alpha =2$，典型的 EM SIRT（方程39） 对应于 $\alpha =0$，是在 Xmipp和TomoJ中实现的，然而ASTRA工具箱有一个 $\alpha =0$ 的 SIRT 算法。

$\alpha =0$ 的情况和可行性问题（feasibility problems）理论建立了有趣的联系。考虑由与第 i 个实验测量兼容的所有体积定义的超平面：
H i = { x ∈ R B 3 ∣ ⟨ a i , x ⟩ = b i } . H_i=\{x\in\mathbb{R}^{B^3}|\langle \mathbf{a}_i,\mathbf{x} \rangle =b_i \}. Hi​={x∈RB3∣⟨ai​,x⟩=bi​}.
解决断层扫描问题相当于找到一个体积 $\mathbf{x}$，使其与所有测量兼容（注意，这里忽略了噪声的影响）：

$$\mathbf{x}\in H_1\cap H_2\cap ...\cap H_{M{P}^2}$$

给定一个体积 ${\mathbf{x}}^{(k)}$，我们可以将其正交投影到由第 i 个测量给出的超平面上：

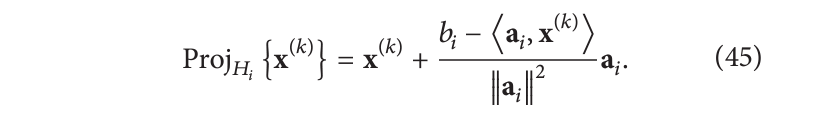
这样，可以将 $\alpha =0$ 的SIRT迭代重写为：

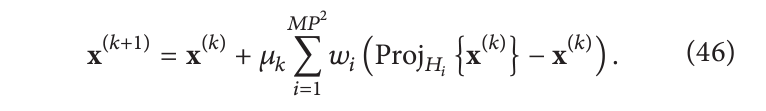
也就是说，在每次迭代中我们使用当前解到由实验测量定义的超平面集的正交投影的加权和来更新体积。松弛因子 ${\mu }_k$ （通常在0和1之间选择，虽然0到2之间的值有收敛定理）可以理解为我们从当前位置 ${\mathbf{x}}^{(k)}$ 到所需位置 P r o j H i { x ( k ) } Proj_{H_i}\{\mathbf{x}^{(k)}\} ProjHi​​{x(k)}。在有噪音的情况下，我们可能会更加保守并使用较小的松弛因子，这反映了我们对实验测量的不信任。

实际上，我们可以在一次超平面投影之后更新对当前解的估计，也就是说不必等待同时看到所有测量结果，但我们可以在看到每个像素值后立即更新体积。

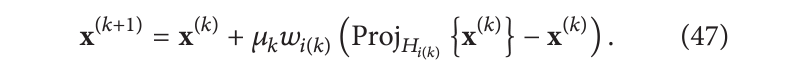
索引 i(k) 会覆盖所有实验测量结果。该方案被称为 ART （代数重建技术）， SIRT 和 ART 之间的差异与线性方程组解中的 雅克比更新（SIRT）和高斯-赛德尔更新（ART）之间的差异相同。在 ART 情况下，一旦获得新的可用信息就会更新体积。可用利用 ART 这一特性，在采集数据时以流式模式使用 ART，并在重建达到特定标准时立即停止数据采集（这里以最小化辐射损伤）。ART 的收敛速度比 SIRT 快得多，尽管它往往会产生稍微有噪声的重建。通过选择随时间减小的松弛因子可以缓解此问题。Block-ART 和 Simultaneous ART (SART) 给出了查看每个像素后更新和查看所有像素后更新的权衡策略。

体积在看到一小组像素后更新（通常是同一实验图像中的所有像素）。

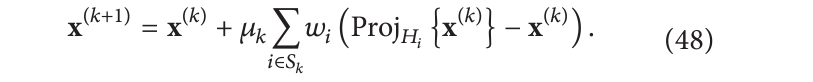
Kunz等[73]研究了这些块的选择顺序如何影响重建的质量。此外我们不需要局限于正交投影，也可以进行倾斜投影。给定一个对称的正定矩阵 $G$，超平面 $H_i$ 上的倾斜投影（oblique projection）定义为：

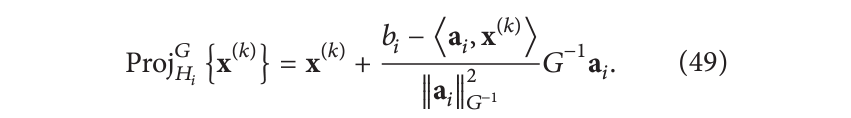
对这些替代方案的研究促进了一系列迭代算法的出现（Cimmino，Component Averaging(CAV)，Block-iterative CAV (BiCAV)， Block-Simplified SART，带Bregman投影的迭代算法，块迭代欠松弛熵投影，Averaging Strings等）。
ART的一个变体 multiplicative ART(MART)，其中迭代步骤是惩罚而不是加法。尽管其中一些算法研究在 EM 中进行了测试，但这些更先进的变体都没有得到大规模采用。对于代数重建法的综述可以参考[100-102]。

所有的 SIRT 算法可以写成紧凑矩阵形式：

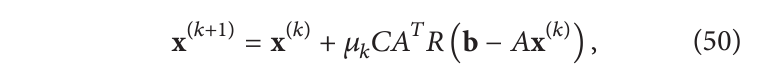
其中A为系统矩阵（$A$ 将解的当前估计值投影到图像投影空间，而 $A^T$ 将残差反向投影到体积空间），$R$ 和 $C$ 为合适的对角矩阵（$C$ 作用于基函数空间 $c_{jj}=1/{\gamma }_j$，$R$ 作用于实验测量空间 $r_{ii}=w_i/{\rho }_i$）。

以这种矩阵形式表示，我们可以很容易地找到另一种在图像处理中非常流行的SIRT算法： Landweber迭代。加权最小二乘法的一种可能解决方案，

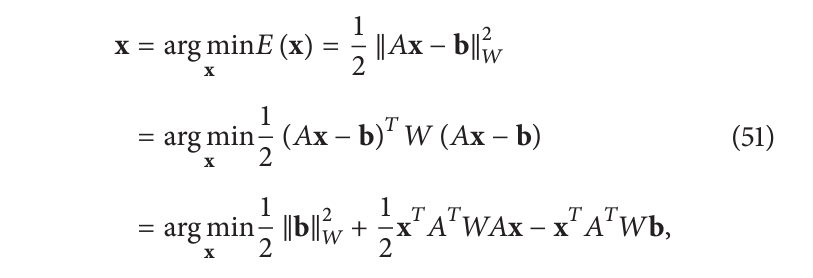
就是使用梯度下降迭代：

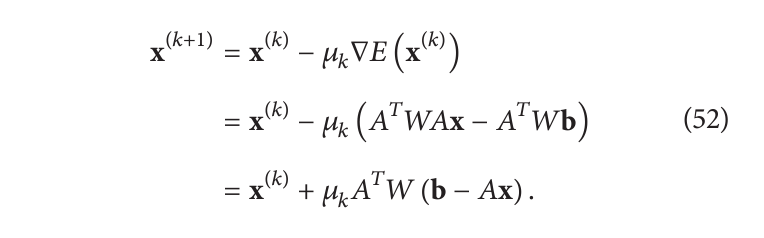
后一个迭代称为 Landweber 迭代，可以很容易地看出它符合通用(方程50)的 SIRT 形式。

这类传统算法的另一个有趣变体是可以使用不匹配的投影，例如，一个相对复杂的前向投影A，包括投影几何和多个离焦效应，以及一个简单的后向算子B，只考虑投影几何：
$${\mathbf{x}}^{(k+1)}={\mathbf{x}}^{(k)}+{\mu }_{k}C{B}^{T}R(\mathbf{b}-A\mathbf{x})$$

这类算法的收敛性取决于矩阵 $I-C{B}^{T}RA$ 的特征值。
在EM中该策略已在Xmipp中实现（前向投影考虑几何和CTF，但后向投影仪只考虑几何）。尽管已证明该方法可以成功恢复底层3D结构，但由于大多数迭代算法都存在普遍问题：和直接傅里叶反演算法相比计算速度较慢，因此该方法尚未得到进一步研究。

近年来，求解线性方程组最流行的算法之一是共轭梯度法。该算法的成功之处在于能够在 $B^3$ 步内收敛到局部解（步数和所寻求解的维数相同）。注意这个数字是有限的，比 ART 和 SIRT 的步数小得多，后者的收敛定理在迭代次数趋于无穷大时处于极限。给定方程：
$$\mathcal{A}x=b$$

诀窍在于使用一组方向 { p k } \{p_k\} {pk​}，这些方向相对于由A导出的内积是正交的（$k\ne k^{\prime }=>⟨p_k,p_{k^{\prime }}{⟩}_A=0$），这些方向被成为相对于A的共轭方向。然后所求的解可以写成以下形式：

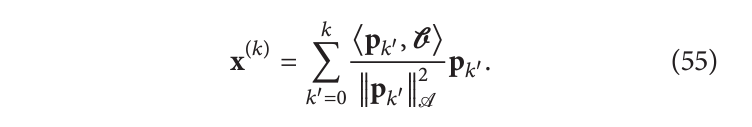
共轭方向的集合也迭代地构造为：

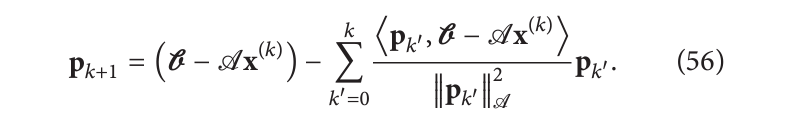
实际上这些求和可以被很好地重组，这样在实现时只要保留一个当前解的向量，一个残差的向量和一个当前共轭方向的向量。

在EM背景下，[59]在傅里叶空间中使用了共轭梯度方法，然而基本的共轭梯度算法有很多变种（如共轭残差、双共轭梯度、稳定双共轭梯度、Lanczos方法、广义最小残差法、双 Lanczos、共轭梯度平方、准最小残差等；其中大部分属于 Krylov 子空间算法家族），这些算法尚未在EM中测试。

实际上这些迭代算法都不会运行到完全收敛。相反，这些算法通常运行固定的迭代次数（在Block ART的情况下通常为M或2M次，在CG的情况下为20次，在SIRT的情况下为100-150次）。这些算法在目标函数中更新多少次取决于方程系统的条件数：
$$k(\mathcal{A})=\frac{{\sigma }_{max}}{{\sigma }_{min}}$$
这里的 $\sigma$ 是矩阵A的最大和最小奇异值。如果这个比例接近1，迭代算法将很快收敛到误差函数的最小值。如果该比例远大于1，则该问题被称为 ill-posed 问题（b向量中的小扰动可能会转化为解向量x中的大变化）并且迭代算法的收敛速度较慢。在求解normal方程时有：

$$k(\mathcal{A})=k(A^{T}A)=k^2(A)$$
也就是说矩阵A的不适定性恶化了。因此，在线性方程求解理论中，通常使用预条件矩阵P，这样就不用求解问题：
$$\mathcal{A}x=\mathcal{C}$$
而是：
$$P^{-1}\mathcal{A}x=P^{-1}\mathcal{C}$$

预处理矩阵P的选择方式如下：
$$k(P^{-1}\mathcal{A})<k(\mathcal{A})$$
尽管已经在不同类型的断层扫描装置中测试了几种预处理器，在EM中还没有尝试使用任何预处理器。

受约束的三维重建

$$\mathbf{x}\in H_1\cap H_2\cap ...\cap H_{M{P}^2}$$
可以用一些额外的约束来补充上面公式的可行性问题，这些约束代表了关于重建的先验知识。我们可以通过施加体积属于某个凸集的事实来实现这一点（如果对于集合中的任意两个体积 $x_1$ 和 $x_2$，它们的线性组合 $(1-\lambda )x_1+\lambda x_2$，其中$0\le \lambda \le 1$，也属于该集合，则该集合是凸的。所有非负体积的集合是凸的，所有在掩模里定义的体积的集合也是凸的，具有给定对称性的所有体积的几何，以及限定在给定频率范围内的所有体积的集合等也是凸的。给定一组表示我们对重建粒子的先验知识的凸集$C_1,C_2,...C_K$，可以尝试在这些凸集的交集中找到一个可行的体积
$$\mathbf{x}\in H_1\cap H_2\cap ...\cap H_{M{P}^2}\cap C_1\cap C_2...\cap C_K$$

这个问题在EM社区被广泛研究，称为投影到凸集（POCS）。该方法的基本思想是交替进行投影：一方面投影到由实验测量定义的子空间(Hi)，另一方面是投影到凸集上（将负值全部置为0的投影器将非负体积集上的负值全都置为0；将当前解应用到mask上的投影器将mask应用到当前解；将当前解对称化的投影器对当前解进行对称化；将当前解应用低通滤波器的投影器将带限体积集上的低通滤波器应用到当前解等）。在信号处理领域，POCS算法已通过使用邻近运算符的算法进行了推广。尽管超出了本综述范围，但这些算法尚未在EM中引入。

Landweber 迭代也可以在约束设置中设置。假设我们已知先验是x位于凸集C中。那么约束问题的解
$$\mathbf{x}=argmi{n}_{\mathbf{x}\in C}\frac{1}{2}\Vert A\mathbf{x}-\mathbf{b}{\Vert }_W^2$$
可以通过迭代算法找到：

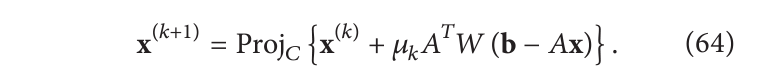
如上面的两个示例，这种约束优化最有趣的想法之一是可以在标准断层扫描更新 $({\mathbf{x}}^{(k)}+{\mu }_k{A}^{T}W(b-A\mathbf{x}))$ 和凸集上的投影 $(POCS,Pro{j}_C)$ 之间进行交替。

这些约束优化的思想可以进一步拓展到不可微的凸函数（残差的$l_1$范数就是这种函数）。让我们假设正在最小化不可微分的凸函数 $\varphi (\mathbf{x})$:
$$\mathbf{x}=argmin\varphi (\mathbf{x})$$

在可微点 $\varphi$ 处，梯度下降迭代很适合寻找目标函数的最小值：

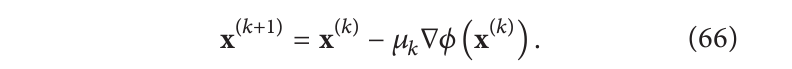
不可微分点（通常出现在凸集交集的边界处）的问题是梯度没有明确定义。我们可以定义次梯度。向量 ${\mathbf{g}}_k\in {\mathbb{R}}^{B^3}$ 是 $\varphi$ 在 ${\mathbf{x}}^{(k)}$ 的子梯度，如果对于任意 $\mathbf{x}$ 我们有：

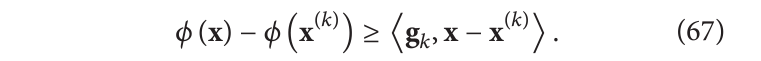
直观上，梯度在可微点处定义了一个和 $\varphi$ 相切的唯一超平面，并且由于 $\varphi$ 是凸面，所以该切平面始终低于 $\varphi$ 。在不可微点处，有无数个超平面接触 $({\mathbf{x}}^{(k)},\varphi ({\mathbf{x}}^{(k)}))$ 且低于 $\varphi$。这些超平面的法向量构成了次梯度的集合。然后，在这些不可微分点处，次梯度方法迭代为：
$${\mathbf{x}}^{(k+1)}={\mathbf{x}}^{(k)}-{\mu }_k{\mathbf{g}}_k$$
我们可以轻松地向该方法添加凸约束，以获得约束次梯度最小化（称为投影次梯度最小化，Projected Subgradient minimization）

x ( k + 1 ) = P r o j C { x ( k ) − μ k g k } . \mathbf{x}^{(k+1)}=Proj_C\{\mathbf{x}^{(k)}-\mu_k\mathbf{g}_k\}. x(k+1)=ProjC​{x(k)−μk​gk​}.

优越化（superiorization）被提出作为投影次梯度法的代替方案。优越化的思想是引导重建迭代朝向约束条件。投影次梯度法和优越化之间的主要区别之一是如果存在多个凸约束，投影次梯度法需要投影到它们的交集中，即可行集，而优越化只需要依次投影到每个约束条件上。注意，交集可能是空的。例如，在有限支持掩模内定义并带限的所有体积的集合是空的。此外，投影到并集的投影器可能比投影到每个单独约束的投影器更复杂。这限制了投影次梯度法的适用性，而这对优越化来说不是问题。尽管这些算法在断层扫描社区中是可用的，但尚未在EM领域得到应用。

在EM中，对受约束优化的另一种方法是定义新的方程，这些方程必须与来自测量的方程系统一起同时求解。例如，可以用基函数来容易地表示一个掩模。假设在给定位置 $r_0$ 没有来自分子的密度，那么可以在 $r_0$ 特化级数展开并添加线性方程：

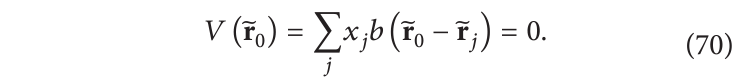
通过这种方式，我们处理了来自掩模、对称性、总分子质量和非负性的先验知识。当投影数量较少时，添加这些先验信息确实很有意义。然而随着投影数量的增加，先验信息带来的改进变得不是那么显著，表明大部分信息以及存在于实验数据集中。现在，随着对高分辨率结果的不断追求，再次有机会探索这些可用的额外信息来源，尽管目前这条研究路线尚未被重启。

迭代引导算法往往会促进具有某些特征的重建。例如，[65,71,72,127,128]关注于重建离散值对象的问题（重建的体积只能有少数几个值，通常是两个（背景和前景））或者只有很少活跃体素的对象。它们使用的投影器类似于在凸集中的那些投影器，例如，bgART 定义了如下投影器：

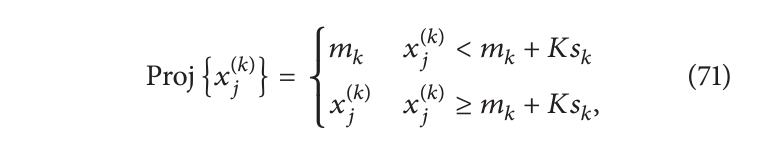
其中，$m_k$是第i次迭代中背景灰度值的估计均值，$s_k$是其估计标准差，$K$ 是用户选择的倍数（通常在3到6之间）。这些迭代引导算法和投影到凸集的算法之间的主要区别在于，前者投影到非凸集上，此外，重建投影的集合在每次迭代中都会改变。这类算法的收敛性在[129]中进行了研究。[75]中提出了一种用于电子断层扫描的算法，其中引导由非线性扩散去噪算法驱动。在每次重建步骤之后，通过应用非线性扩散算法的一步（投影器）来对重建体积进行去噪。为了使这些引导算法收敛，重建算法必须具备“抗扰动性”，且扰动必须“小到不会破坏重建算法的工作”。

稀疏3D重建

在过去的十几年里，稀疏表示一直是图像和信号处理领域最活跃的研究方向之一，其思想是，自然图像和对象在某些适当的空间中可以用很少的非零系数来表示。这个空间可以是固定的（例如小波变换或离散余弦变换），也可以针对特定问题计算的（基于字典的算法）。知道我们的对象具有稀疏表示可以帮助算法将能量集中在少数系数上，防止因噪声通常引起的能量分散。在这个问题设置中，通常使用不同于欧几里得范数的向量范数。通常使用的是 $l_p$ 范数：

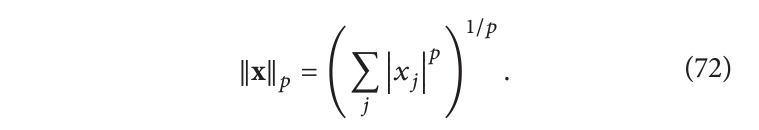
当 $p=2$ 时是欧几里得范数，$p=1$ 时是曼哈顿范数，当 $p=0$ 时向量的范数仅仅是向量中非零系数的个数（严格来说不算是范数）。稀疏性的目标是找到 $\mathbf{x}$ 的一种表示形式，使得：

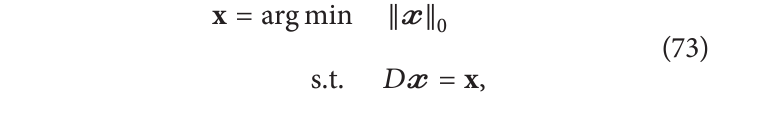
其中，D是用于表示 $\mathbf{x}$ 的元素字典（小波、DCT或特定问题的字典），$x$ 是 $\mathbf{x}$ 在该字典中的表示。目标是使尽可能少的系数不为0。如上所述，稀疏表示在 $l=0$ 范数中最有趣。然而将这种范数加入目标函数需要组合优化技术，而这在计算复杂度上是NP难的。有趣的是，$0<p<2$ 的 $l_p$ 范数倾向于促进稀疏表示（ $x$ 具有相对较少的非零系数），并且在近年来以及开发出高效的算法来进行这些最小化。

我们将回顾的第一类算法设计 $l_0$ 范数，并解决以下两个相关问题中的任意一个：

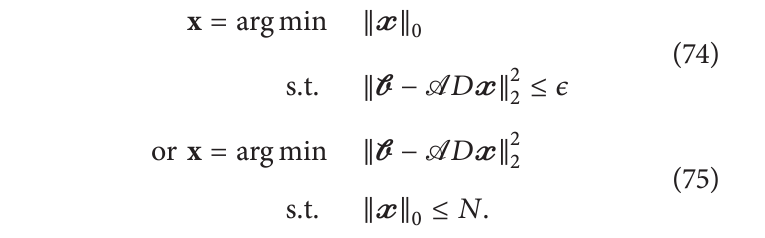
请注意，我们的“断层字典”（$\mathcal{A}D=A^{T}AD$）包括标准字典表示 $D$ 以及断层设置的投影结构信息 $\mathcal{A}=A^{T}A$
。在下面，我们把这种断层字典称为 $\mathcal{D}$，它的第 $j$ 列表示为 $d_j$（在字典术语中，这将是第j个原子，假设字典中有 $J<<B^3$ 个原子）。许多不同的算法可以解决该问题，但没有在EM中测试过。其中，匹配追踪（Matching Pursuit）和正交匹配追踪是两个最流行的方法（实际上后者曽被从事EM研究的人在断层扫描设置中测试过，但没有应用于 EM 数据）。为了简单起见，我们展示匹配追踪的迭代过程，以说明这些算法的特点及其与迄今为止介绍的迭代算法的不同之处。

另 $x^{(k)}$ 表示现在的重建。在第一次迭代时， $x^{(0)}=0$. 现在我们选择和我们方程系统的残差 $r^{(k)}$ 最大对齐的原子（注意 $r^{(0)}=b$），计算其系数并更新残差。这个过程迭代进行直到达到所需的原子数量。以下算法从 $k=0$ 执行到 $k=N-1$。

• Step1. 找到和该残差最大对齐的原子
• Step2. 通过将残差投影到该原子上来更新当前解
• Step3. 更新残差

该算法是贪心算法，找到的是重建问题的次优解。然后它非常容易实现。正交匹配追踪通过修改第2步提供了显著的改进，在这一方法中，通过将b正交投影到目前使用的所有原子所跨越的子空间上来更新所有系数。

第二类算法用 $l_1$范数代替 $l_0$ 范数。

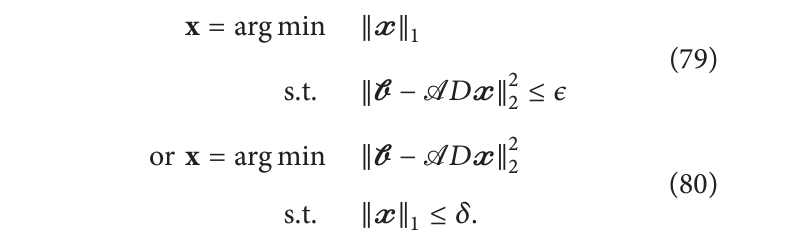
这允许采用更高效的优化算法。经典算法包括最小绝对收缩和选择算法（Lasso，也称为基追踪）、迭代重加权最小二乘法（IRLS）、迭代收缩算法、最小角回归（LARS）及其任何变种。由于其简洁性，迭代收缩算法已被引入电子显微镜。然而EM版本的算法旨在解决正则化问题：

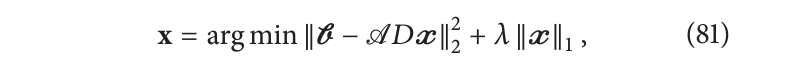
而不是上面提到的受约束问题。在其最简化的形式中，这些算法在标准重建更新（例如采用一个SIRT步骤）和在某个合适的稀疏空间（例如小波空间）中的软阈值步骤之间交替进行。其基本原理相对简单，类似于迭代引导算法的思路。在应用标准重建步骤之后，通过将某些已知能够促进稀疏性的空间（例如小波空间）中的所有小系数设置为0，将解引导到稀疏解。一个基本的迭代步骤如下：

在上述迭代中，我们假设了一个正交字典或变换，但对于非正交字典也可以找到等效的公式。

使用拉格朗日增强的目标函数形式在数据分析中是一个常用技术：
$$\mathbf{x}=argmi{n}_{\mathbf{x}}F(\mathbf{b}-A\mathbf{x})+\lambda G(\mathbf{x})$$

第一项 F 是 数据保真项，第二项 G 是正则项。很多不同的方案都是这种结构。例如一个典型的正则化加权最小二乘法问题可以通过Tikhonov二次正则化（也称为岭回归）来表示。该正则化涉及一些预处理矩阵 L:
$$\mathbf{x}=argmi{n}_{\mathbf{x}}\Vert \mathbf{b}-A\mathbf{x}{\Vert }_W^2+\lambda \Vert L\mathbf{x}{\Vert }_2^2$$
其 normal equations 是：
$$(A^{T}WA+\lambda L^{T}L)\mathbf{x}=A^{T}W\mathbf{b}$$
假设测量值存在高斯误差，体积系数存在高斯先验，我们将有 $L={\sum }_{\mathbf{x}}^{-1/2}$。
$$(A^{T}WA+\lambda \sum _{\mathbf{x}}^{-1})\mathbf{x}=A^{T}W\mathbf{b}$$

如果我们认为 $\mathbf{x}$ 和 $\mathbf{b}$ 是在傅里叶空间中，那么这些将是与Relion正在解决的相同贝叶斯问题相关的 normal equation。矩阵W包括CTF信息，矩阵A包含数据采集的几何信息（包括每个投影具有给定投影方向和位移的概览），矩阵 ${\sum }_x$ 表示我们关于傅里叶空间中系数能量的先验信息。Relion 和这些 normal方程的一个区别在于其在每次迭代后都会重新估计先验信息。

我们可能还可以更进一步考虑广义Tikhonov正则化

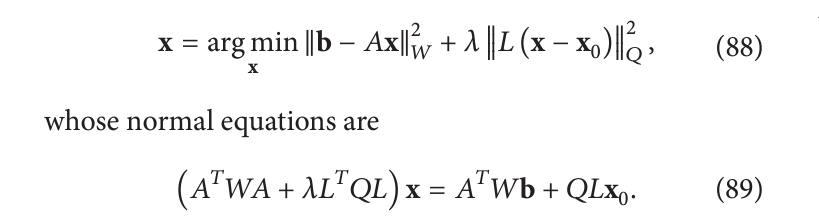
如果假设预处理系数之间的独立性，则大多数最大后验（MAP）算法可以写成：
$$G(L\mathbf{x})=\sum _j\varphi ((L\mathbf{x}{)}_j)$$
这里 $\varphi (\mathbf{x})$ 是先验，x的负对数似然 （$\varphi (\mathbf{x})=-log{p}_{\mathbf{x}}(x)$）。假设 $\mathbf{x}$ 系数的高斯分布导致 $L={\sum }_{\mathbf{x}}^{-1/2}$ 和 $\varphi (\mathbf{x})={\mathbf{x}}^2+C$（C是常数不影响MAP优化）。假设标准差 $\sigma$ 呈中心拉普拉斯分布导致 $L=(1/\sqrt{2}\sigma )I$ 和 $\varphi (x)=|x|+C$。在EM中，[74]假设了一种中值根先验（Median Root Prior），该先验有利于局部单调的重建。

如果我们将 $L$ 视为体积导数算子，并将G视为该导数的 $l_1$范数（即导数系数上的拉普拉斯先验），
$$G(\mathbf{x})=\Vert L\mathbf{x}{\Vert }_1$$

然后我们就有了全变分正则化（也叫 TVL1）。 $l_1$ 范数的问题是无法微分，有时它被替换成：

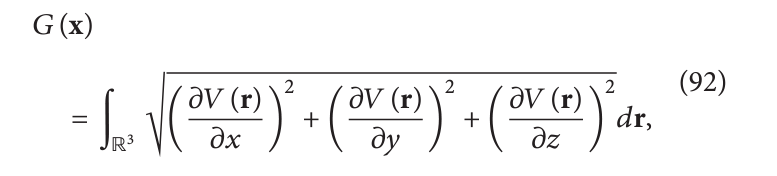
其中 $V(\mathbf{r})$ 是使用 x 系数重建的体积，这在EM领域在[62][63][66][57][76]中探索过。

[140]中的方法也属于正则化类型。函数 G 是从稳健统计中借用的 Huber 函数：

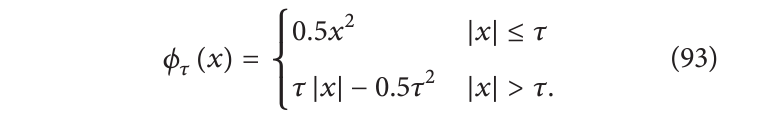
这个函数介于二次惩罚和线性惩罚之间（$\tau$来控制二者之间的切换）。对于低导数值，该函数表现为二次项，对于高导数值，它表现为线性项。其目的是防止大导数在优化过程中占主导地位。

可以看到上述正则化问题要么包含关于体积 $\mathbf{x}$ 的一些先验知识，要么包含该体积的某种性质（$L\mathbf{x}$，通常是其导数）。然而我们可以通过一种新算法（交替方向乘子法，ADMM），同时包含这两种。这种算法最近被引入电子显微镜领域：

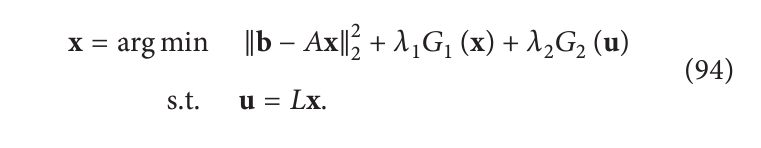
实际要解决的问题是增强拉格朗日：

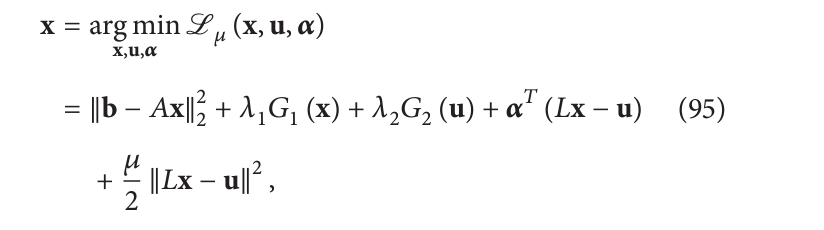
这里 $\alpha$ 是拉格朗日乘数的集合。 ADMM 迭代进行：

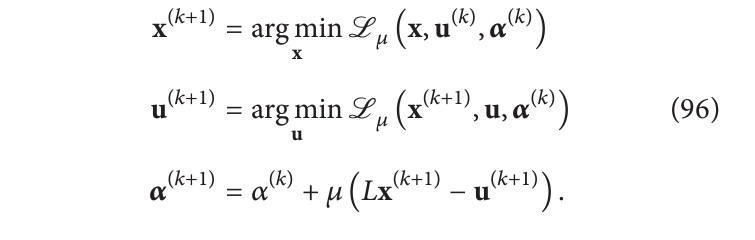
和这些稀疏重建问题相关的是压缩感知问题。其思路是进行二维或三维重建时，不是从完整图像开始，而是从投影图像中的一些不相关的点来时[142-144]。诀窍在于先验知识表明解是稀疏的，这使得可以从比奈奎斯特定理要求的更少的点重建完整的图像或体积（存在一个测量数量的下限）。这种理论尚未在生物电子显微镜应用中得到探索，但在材料科学电子显微镜中已有研究，特别是在使用扫描透射电子显微镜（STEM）时。对于生物样品，能量过滤透射电子显微镜（EFTEM）是一个明显可以受益于压缩感知采集的候选者。

结论

迭代重建算法领域已经得到了广泛研究，特别是在电子显微镜数据的应用中，如我们在这篇综述中所展示的。三维重建问题不再是SPA的瓶颈。尽管将数据和先验知识相结合的尝试不多见，可能由于较高的计算成本。然而随着接近更高的分辨率，重新探讨这条研究路线以提高重建分辨率可能是值得的。

在电子断层扫描中不太一样，因为最大倾斜角限制、金颗粒的存在以及投影数量少导致了重构伪影的产生。此外，特定的数据采集几何（通常为单轴倾斜）有利于采用纯二维重建方法，从而减少一个维度的重构问题，极大地降低了计算成本。在这一领域，能够结合先验信息的迭代算法仍然是一个非常活跃的研究领域。传统的迭代算法如ART和SIRT仍然占据主流地位。然而，结合凸、非凸和稀疏性约束的更现代的强大重建算法不断出现，很可能在不久的将来，会有新的标准。

---

$$Author:Chier$$