（二）背景知识 -- 1 Huffman树与Huffman编码

1. Huffman树与Huffman编码

1.1 Huffman树

1.1.1 背景

在介绍赫夫曼编码前，需要介绍赫夫曼树，而介绍赫夫曼树，就不得不提到美国数学家赫夫曼(David Huffman) ， 也译为哈夫曼。

他在1952年发明了赫夫曼编码，为了纪念他的成就，于是将他在编码中用到的特殊二叉树称为赫夫曼树，将他的编码方法称为赫夫曼编码。

也就是说，我们现在介绍的知识全都来自于近60年前这位伟大科学家的研究成果，而我们平时所用的压缩和解压缩技术也都是基于赫夫曼的研究之上发展而来的。

1.1.2 概念

为了更好地理解相关概念，以将学生的成绩（0-100分）划分为不及格（0-59分）、及格（60-69分）、中等（70-79分）、良好（80-89分）、优秀（90-100分）五个等级为例进行说明。

若逐级而上进行判断，有以下二叉树：

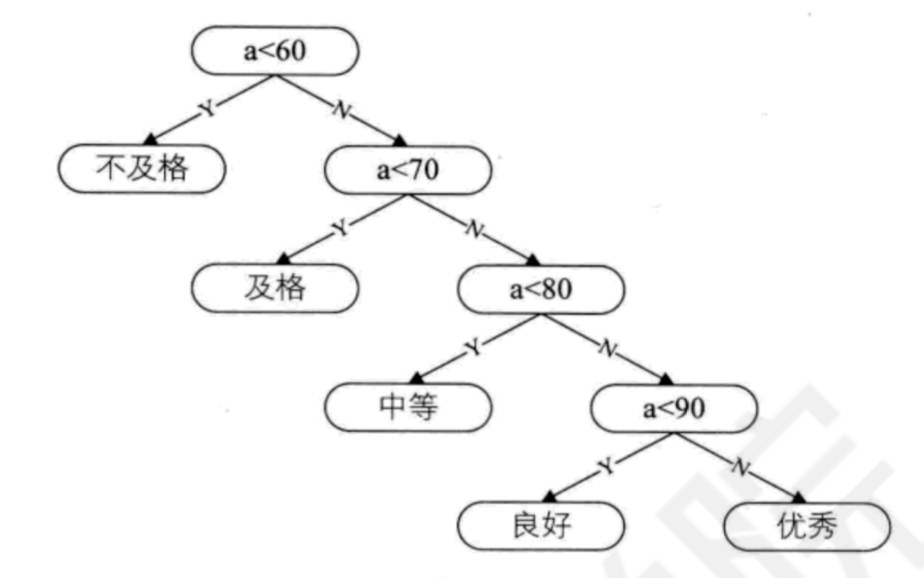
为提高判断效率，结合各分数段所占比例，设计了效率更高的二叉树：

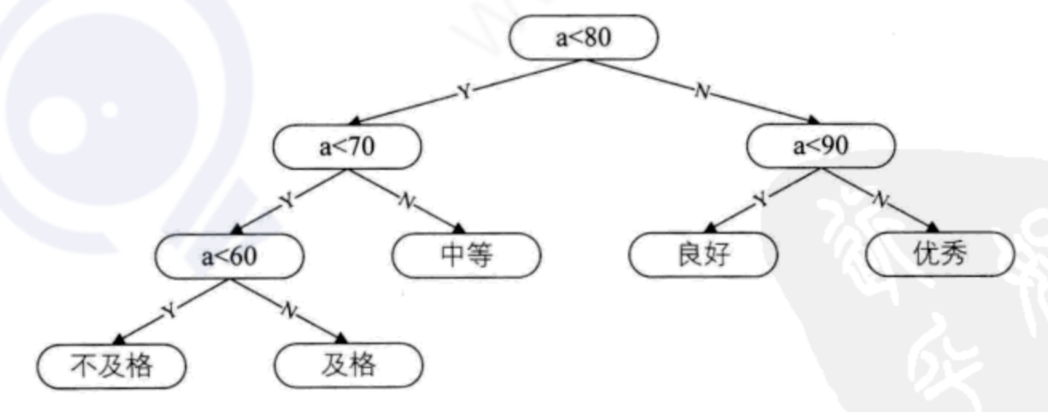
将上述两棵二叉树简化为叶子结点带权的二叉树，A表示不及格、B表示及格、C表示中等、D表示良好、E表示优秀。每个叶子的分支线上的数字，为五级分制的成绩所占比例数，有下图：

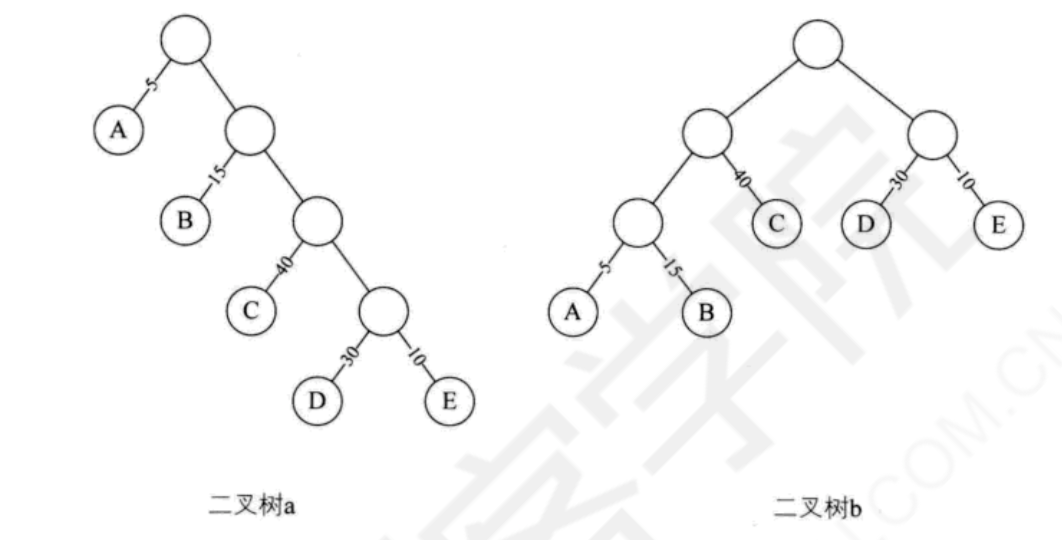
• 路径/路径长度
  从树中一个结点到另一个结点之间的分支构成两个结点之间的路径。
  路径上的分支数目称做路径长度。
  树的路径长度，就是从树根到每一结点的路径长度之和。
  路径长度通常针对根节点而言。设根节点层数为1，那么，根节点到$L$层节点路径长度为$L-1$。
  如上图所示：二叉树a中，根结点到结点D的路径长度为4；二叉树b中，根结点到结点D的路径长度为2；二叉树a的树路径长度为1+1+2+2+3+3+4+4=20；二叉树b的树路径长度为1+2+3+3+2+1+2+2=16。
• 结点的带权路径长度
  考虑到带权的结点，结点的带权路径长度为，从该结点到树根之间的路径长度与结点上权的乘积。
• 树的带权路径长度
  树中所有叶子结点的带权路径长度之和。
• Huffman树（最优二叉树）
  假设有n个权值 {$w_1,w_2,...,w_n$}，构造一棵有n个叶子结点的二叉树，每个叶子结点带权$W_k$，每个叶子的路径长度为$l_k$，则其中带权路径长度 $WPL$ 最小的二叉树称作赫夫曼树。
  如上图所示：
  二叉树a的WPL=5×1+15×2+40×3+30×4+10×4=315；
  二叉树b的WPL=5×3+15×3+40×2+30×2+10×2=220。
  这意味着，假设有10000个学生的百分制成绩需要计算五级分制成绩，用二叉树a的判断方法，需要做31500次比较，而二叉树b只需22000次比较。

1.1.3 构造

步骤

如何构造Huffman树，结合上述示例，具体步骤如下：

(1) 将有权值的叶子结点按从小到大的顺序排列成一个有序序列，即：A5，E10，B15，D30，C40。
(2) 取头两个最小权值的结点作为一个新节点$N_1$的两个子结点，其中相对较小的是左孩子，此处A为$N_1$的左孩子，E为$N_1$的右孩子。新结点的权值为两个叶子权值的和5+10=15，如下图所示：

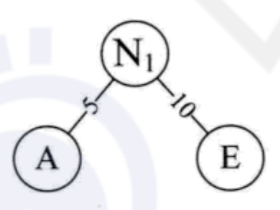
(3) 将$N_1$替换A与E，插入有序序列中，保持从小到大排列。即：$N_1$ 15，B15，D30，C40。
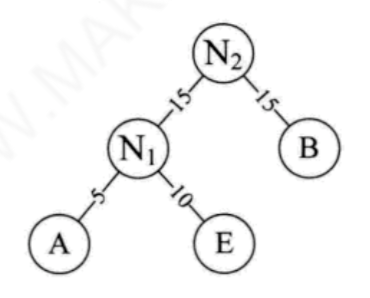
(4) 重复步骤2。将$N_1$与B作为一个新节点$N_2$的两个子结点。$N_2$的权值=15+15=30，如下图所示：

(5) 将$N_2$替换$N_1$与B，插入有序序列中，保持从小到大排列。即：$N_2$ 30，D30，C40。
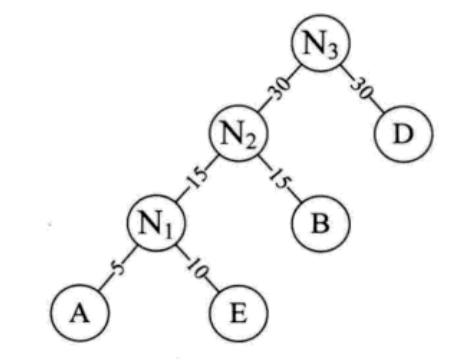
(6) 重复步骤2。将$N_2$与D作为一个新节点$N_3$的两个子结点。$N_3$的权值=30+30=60，如下图所示：

(7) 将$N_3$替换$N_2$与D，插入有序序列中，保持从小到大排列。即：C40，$N_3$ 60。
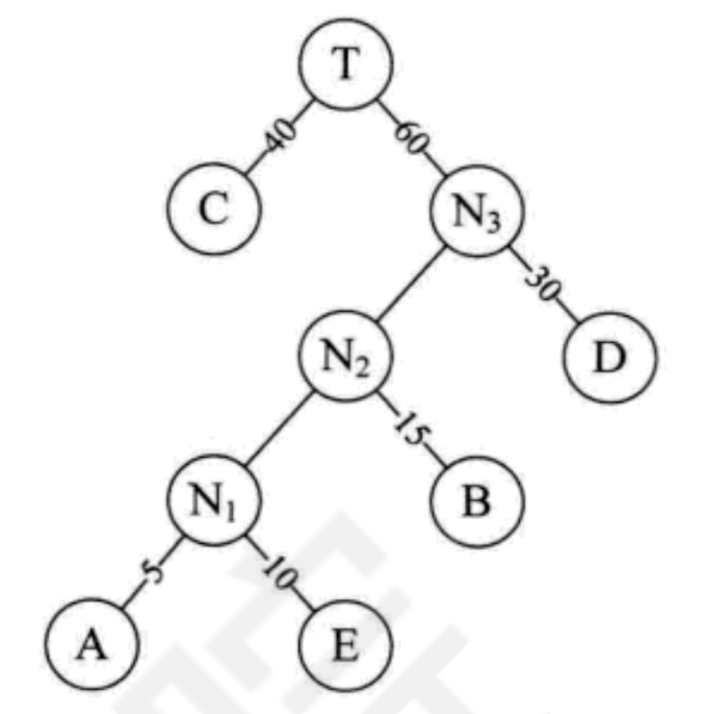
(8) 重复步骤2。将C与$N_3$作为一个新节点$T$的两个子结点。由于T即是根结点，完成赫夫曼树的构造。如下图所示：

算法

结合上述步骤，可将构造Huffman树的算法描述总结如下：

(1) 根据给定的n个权值 { w 1 , w 2 , . . . , w n } \{w_1,w_2, ... , w_n\} {w1​,w2​,...,wn​} 构成n棵二叉树的集合 F = { T 1 , T 2 , … ， T n } F=\{T_1, T_2, …，T_n\} F={T1​,T2​,…，Tn​}，其中每棵二叉树$T$中只有一个带权为$w$根结点，其左右子树均为空。
(2) 在$F$中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。
(3) 在$F$中删除这两棵树，同时将新得到的二叉树加入$F$中。
(4) 重复2和3步骤，直到$F$只含一棵树为止。这棵树便是赫夫曼树。

1.2 Huffman编码

数据通信中，需要将传送的文字转换成二进制的字符串，用01的不同排列表示字符。二进制编码大致有两种方式：等长编码和变长编码。

等长编码即所有字符的编码长度相同，如果有6个字符，那么就需要3位二进制（$2^3=8>6$）。由于等长编码对于所有字符的编码长度相同，因此对于一些出现频率极高的字符来说，等长编码会造成数据压缩率不高。

变长编码可以达到比等长编码好的多的压缩率，其思想就是赋予高频词短编码，低频词长编码。变长编码中只考虑「前缀编码」，即一个字符的编码不能是另一个字符编码的前缀。

因此，可以用字符集中的每个字符作为叶子节点生成一颗编码二叉树，为了获得传送报文的最短长度，可以将每个字符的出现频率作为字符节点的权值赋予该结点上，然后构造一棵Huffman树。利用Huffman树设计的二进制前缀编码，被称为Huffman编码。

• 一般地，设需要编码的字符集为 { d 1 ， d 2 ， . . . ， d n } \{d_1，d_2，...，d_n\} {d1​，d2​，...，dn​}，各个字符在电文中出现的次数或频率集合为 { w 1 , w 2 , . . . , w n } \{w_1,w_2, ... , w_n\} {w1​,w2​,...,wn​}，以 { d 1 ， d 2 ， . . . ， d n } \{d_1，d_2，...，d_n\} {d1​，d2​，...，dn​}作为叶子结点，以 { w 1 , w 2 , . . . , w n } \{w_1,w_2, ... , w_n\} {w1​,w2​,...,wn​}作为相应叶子结点的权值来构造一棵赫夫曼树。规定赫夫曼树的左分支代表0，右分支代表1，则从根结点到叶子结点所经过的路径分支组成的0和1的序列便为该结点对应字符的编码，这就是赫夫曼编码。

Word2vec算法也用了Huffman编码，它把训练语料中的词当成叶子节点，其在语料中出现的次数当做权值，通过构造Huffman树来对每一个词进行Huffman编码。

参考

博客：Word2Vec-知其然知其所以然
《大话数据结构》 —— 6.12 赫夫曼树及其应用