2.2.2-2原码定点数的力加减法运算-3补码定点数的加减法运算-4符号扩展

 

 

多亏了你我的人生才闪闪发光◠‿◠

XYXZNB

 

 

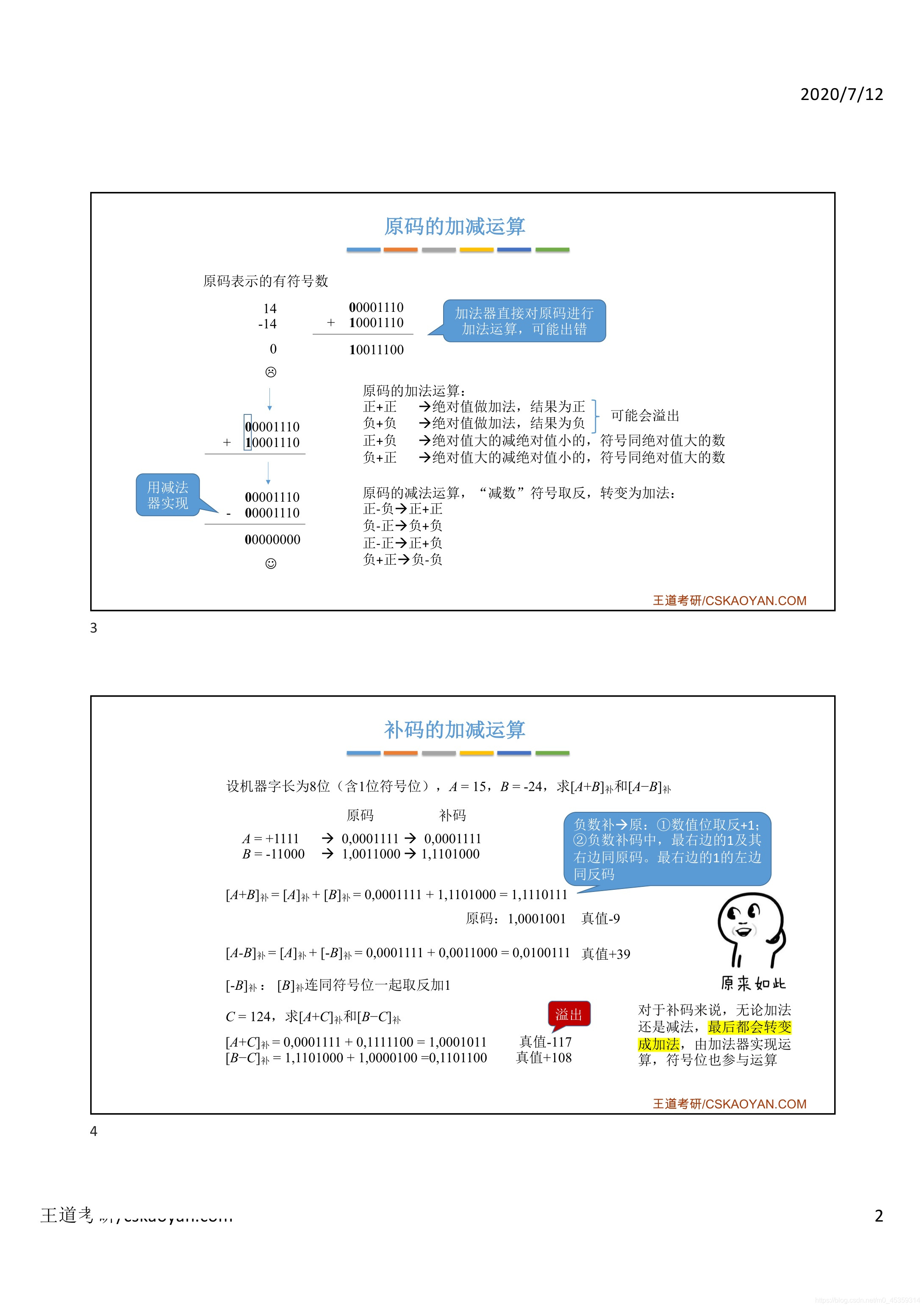
好的这一小节中我们要探讨的是定点数的加减运算，我们之前说过在进行加减运算的时候，我们通常只会探讨原码和补码而反码，一般来说是不会直接参与这种加减乘数运算的，所以我们只探讨元码和补码的加减运算，另外杠精减加或者减的时候有可能会出现溢出的情况，那么计算机硬件是用什么逻辑来判断溢出的呢，这个是我们之后会探讨的问题目那之后我们还会探讨一个符号扩展的问题，首先来看一下源码的加减运算，其实这个部分在之前的小结中我们有简要的探讨过，比如说-14和14这两个数进行相加的操作，那如果加法器直接使用它们的源码进行相加，最终得到的这个结果是一个错误的结果，那我们的处理办法是把-14改为正14，然后加法变成减法，这样的运算用这样的方式来等价，正14+上-14的一个效果，最终就可以得到正确的结果那队员。4的一个效果，最终就可以得到正确的结果，那对于原码的加法来说，左边是被加数，右边是加数被加数，有可能出现两种情况，一种是正数，一种是负数，而加速也有可能出现正和负这样的两种情况，所以源码的加法操作有可能出现4种情况，就是被加数和加数分别为正或者为负的连梁组合好，那首先来看，如果说被加数和加数都是正数的话，此时我们只需要让被加数和加数的绝对值做一个加法，那相加的结果保持为正就可以，而如果是负数加负数，那么同样的用这两个数的绝对值做一个加法符号位啊，保持是负不变，如果被加数是正的，加数是负的，那么我们需要用绝对值大的一个数减掉绝对值更小的一个数最终的符号为何绝对值打了一个数十亿正加速的实测而加速弑父的食物我们丢弃这个硬件进行减法。是负的15，那么我们丢给减法器这个硬件进行减法运算的时候，是把这两个数的绝对值就给了他，并且是绝对值大的一个数，也就15作为被减数，然后剪掉绝对是小的一个，14作为减数，这样我们就确定了数值部分应该是一那最终的结果，符号位应该是和绝对值更大的，这个数保持一致，也就是负的好，最后一种情况，一个负数加上一个正数，那这种情况下处理的方式和上边其实是一样的，同样是要用绝对值更大的那个数减掉绝对值更小的来确定竖直部分，然后符号位和绝对只跟大的那个树宝持一致那源码的，这种加法逻辑，如果用硬件实现的话是很复杂的，接下来我们再来看源码的减法运算，其实减法运算我们最终终归可以把它转变成与之等价的加法运算简述的符号取法这样的话我们就可以把一个转变为假的一个家而转变为我们之前提到的这个逻辑。让操作转变为阏与之等价的一个加法操作，而转变为加好之后，就可以用我们之前提到的这个逻辑来进行处理啊，所以减法操作这就不再多说，另外一点需要注意的是，在进行源码加法的时候，如果a加数和加数它们的符号都是相同的，那么加法之后得到的结果有可能出现溢出的情况，好，那这是原码的加法和减法的一个实现，思路减法，只需要把减数法就可以转变成与之等价的加法，那刚才我们说过原码的加法这么复杂的逻辑，用遍布实现太难了，所以计算机当中通常是用砝码来实现加减运算吧，那这一点我们在之前的小节中同样提过对补码进行加减运算，我们不需要单独的考虑符号位应该怎么处理符号位，同样参与运算就可以啊，来看一下啊，现在有a和B这样的两个数分别是15和负的24表示他们的争执应该是这两个数四表示他们的争执应该是这两个数四现在。5和负的24，那如果用二进制表示它们的真值应该是这样的，两个数4个一表示的是15，然后11000表示的是24，好，现在这个机器字长是8位，其中最高位是符号位，所以我们把a和B两个数不足8位得到他们的源码，再根据源码我们可以求得a和B两个数所对应的补码，那原码和补码的一个转换关系，我们之前已经介绍过了，而现在我们要计算a加B的值，那我们只需要把a和B两个不嘛一起留给加法器，然后加法器会让这个符号位也一同参与运算好，那这样我们就得到了a加B的一个直的补码表示那可以验证一下，我们把这一步吗转变成源码，会发现它所对应的真值是-9也就是15加上不24的一个正确结果，那还记不记得5码如何转变成原码和原码转变成补码的方法是一样的在马的基础上数值为全部取法然后就可以得到与之对应的源码但其实还有一种更快速的转换方式用我们。取法然后末位加1就可以得到与之对应的源码，那其实还有一种更快速的转换方式，用我们上一小节啊推出的这一个规律，对于一个负数来说，负数的补码当中最右边的一个1也就是这个1这个一还有它的右边的部分和原码是保持一致的，而这个一左边的这些部分和反码是保持一致的，所以我们把补码转变成圆满一个更快的方法是找到补码，最靠右的一个一，然后以这个E作为一个分界线，这个分界线左边的这些全部取法就可以直接得到源码，当然了，用之前大家熟悉的方式来转换也是OK的好，那刚才我们探讨的是补码的加法运算，接下来来看一下补码的减法运算如何实现那减法必然是可以转换为加法的a-B可以把它等价为a+负B所以我们这个吗得到了一个布满了这个。那还记不记得，那这个转化方式我们也强调过，只需要把所有的位就符号为在内全部取法，然后没为嘉羿就可以，当然你也可以结合我们刚才介绍的这些方法，要由B的补码求出复辟的不骂，那由于B是一个复数，所以我们可以先求出这个富庶的一个圆满，那从右往左找，到第1个1这画一条分界线，第1个1的左边所有的部分全部取反0001，然后这个一的右半部分全部保持不变，这样的话我们就可以直接得到复B的一个图码表示和我们所有的未取反，然后没为嘉羿而得到的结果是一致的，好，那这我们得到的。得到的值它是一个补法，表示把转换成真值的话就应该是正的39，这就是我们所期待的正确结果，补码的加法和减法的实现最终都会转变成加法，这样的话我们只需要设计一个实现加法的硬件加法器，就可以不需要设计减法器，两个数的补码进行相加，操作的时候符号位也会参与运算好，接下来给大家一个提议，大家可以暂停来练练手，我们引入一个新的变量C，然后a和B就是我们之前给出的这两个值，大家可以试一下a加C和B减C的一个补码运算的结果，可以暂停试一下，好我们来看一下a加C，最终计算的结果是这样的啊，这是C的一个补码，那这个补码所对应的源码是多少呢？我们从最右边这个一的这儿画一条竖线的，然后前边这些数值位全部取反最右边的这个还有他同样保持不变这就是这个吗。部分保持不变符号位同样保持规定，那这就是这个补码所对应的源码，大家可以自己算一下，真值是负的117，好，现在问题发生了，a=15C=124，但是计算的结果，两个正数相加竟然得到了一个负数，那这种现象说明发生了溢出，因为124+15应该是等于139，而我们之前说过8倍的补码，它所能表示的范围只有负的128到镇的127这样的一个范围，所以139这样的一个增值显然已经超出了8位不满可以表示的范围，所以这种情况下就是所谓的溢出皓影一个例子，B减C其实也是一样的，我们通过C的补码求出负C的一个补吗？这样的话就可以把B减C转变成加法运算，那最终得到的这个结果可以看到啊，对应增值是108，同样也是发生了溢出的问题负四减一百二十四已经超出了八位码表示的范围。砝码所能表示的范围两个负数相加，竟然得到了一个正数，好，那既然溢出的状况不可避免，因此计算机硬件就必须考虑到如何处理溢出的问题，所以接下来我们要探讨用计算机硬件实现溢出判断的一个逻辑，当我们对补码进行加法或减法运算的时候，最终都会被转变成加法运算，所以我们只需要考虑补码的加法运算，如何判断溢出就可以好，那一出分为这样的两种，一种叫上一一种叫下移啊，根据这个图很好理解，一个补码，他所能表示的范围是有限的，比如8倍的补码就是负的128，一直到正的127这样的一个范围，那如果两个正数相加，最终的真值超出了127的范围，此时我们就称发生了上亿，那类似的，如果两个负数相加，最终得到的增值啊，小于负的128超出了负数区所能表示的范围，那此时就发生了所谓的下亿，当发生上亿的时候一定是两。唉，那此时就发生了所谓的下一当发生上亿的时候，一定是两个正数相加，最终得到的结果，看起来是一个富庶而发生夏邑的时候，一定是两个负数相加，最终得到的结果，看起来是一个正数，也就是我们刚才提到的这两种情况，那我们可以基于这个规律来设计判断溢出的逻辑，给大家一个例子，大家可以自己体会一下，这儿给出了三位的话所能表示的范围也就是-4~正3这样的一个范围，并且这个地方已经给出了每一个数值所对应的补码到底是多少，那首先第1点只有两个符号，相同的数相加的时候才会发生溢出，这点应该是很好理解的，因为如果两个数比如说1正1负进行相加操作的话，那最终得到的结果只有可能比被加数和加数的绝对值更小，所以两个异号的数相加不可能发生溢出我现在就和这个三位的时候是否一定是正数加证书的复印件。当发生上亿的时候，是否一定是正数加正数，然后最终得到一个负数呢来看一下三位补码，最大可以表示的正数13，如果两个正数相加超过了三这个值，那么此时就发生了上亿，比如说2+2那么2的补码是010，这两个数相加应该是等于00往高位进一个1也就是110，那这个补码对应的是-4这个值，那你会发现从这个数轴上看，在2的基础上再加2，其实相当于从2为出发点往右移动一格，然后再移动一格，移动两格来到了-4这个位置，所以2+2发生了上亿，最终得到的结果是负色，这和我们之前给出的这个结论是相符合的再来看，如果是3+3，那么就是011+011得到结果应该是零一一负二十三百级术上再加三如果结合。3的基础上再加3，如果结合数轴来看的话，就是从这个点出发向右移一格两格三格移动，到了-2这个地方，它的两个正数相加得到了一个负数，那么此时我们就可以判断是发生了上亿的情况好，所以结合这个例子我们可以体会到，当发生上亿的时候，一定是正数加正数，最终得到的结果是一个富庶而发生，下一的时候大家也可以自己验证一下，一定是负数加负数，最终得到的结果是一个正数啊，那基于这个规律计算机硬件如何判断一出呢？先来介绍第1种方法，采用一位符号位计算机进行溢出判断的逻辑表达式，是这样子啊，其中aS表示的是被加速的一个正负号 Ps的一个正负号表示的是最终运算结果的一个政府号这个逻辑表达式计算结果为零的手表是没有一处现在我们来解释一下这个。表示有益处，好，现在我们来解释一下这个逻辑表达式的一个含义，这可能是跨考同学的一个盲点，那如果大家学过离散数学肯定学过这种逻辑的啊，是啊，除了离散数学之外数字电路啊，数电这门课里面也会接触到这种逻辑表达式，包括跨好同学可能没有学过这些内容，所以我们来解释一下，照我们aSBS和SS表示的是逻辑值的真和假，或者说灵合一以这样给出的第1个加法为例，as表示的是被加数的一个符号，也就是0表示逻辑值的甲，然后BS表示的是加数的一个符号，同样是0表示逻辑值的甲，然后最后SS表示的是最终运算结果的一个符号位，符号位为一表示逻辑之地，真也就是这三个逻辑之分别为假假真真，用这种连着写的方式把它们写在一起表示的是这些逻辑值之间执行一个女的运算。写的方式把它们写在一起，表示的是这些逻辑值之间执行一个语的运算，那这的语运算其实就是大家熟悉的C语言里的且的一个操作，几个逻辑值进行与运算的时候，只有所有的逻辑值都为真，都为一的时候，最终相余的结果才是一只要其中任何一个尾角最终都会等于角画，好同学可以联想一下，你编程的时候写if语句你是不是会写啊，某某某某条件且某某条件再切某某条件对吧，只要其中的某一个条件不成立为讲的时候，那么这个逻辑运算最终的结果肯定都是讲，只有所有条件都满足，都为真的时候最终得到结果才是真呐，这是与运算的一个逻辑，而在这个式子当中，除了把这些逻辑值并排着写之外，啊，这还有一个加号，但是这个加号表示的是逻辑的或运算，也就是大家编程的时候会用到的或这个运算服务。编程的时候会用到的货，这个运算符啊，猫条贱货某条件再获猫条，见如果多个条件进行或运算的话，那么只有所有的这些条件都不成立都没讲啊，或者说都为0的时候，这个后预算的结果才是0，而只要其中一个或者多个呃，条件能够满足为真或者说唯一的话，那这个或预算的结果就是1啊，最后这个式子当中还会涉及到逻辑非运算在一个逻辑值的上面画，上一横表示一个非运算，其实非预算就是大家写代码的时候会用到的是感叹号，感叹号，然后某一个条件对吧，呃，其实就是指这个条件真假，取一个烦，这就是非运算，它的效果就是0变11变0号，那弄清楚与或非这三个基本的逻辑运算之后，来看一下这个逻辑运算的式子，最终得到的结果基于这儿的第1个式子被家属和加速的符号位都为零最终得到结果而最终。符号位为1，而最终的这个结果需要进行一个非运算，也就是会把1变成0号，那左边这一整块的运算就是三个0进行与运算，那显然这个与运算最终得到的结果是0再来看右半部分本来是001噢，现在as和BS会分别进行一个非运算，零会变成1，那这样的话，右边部分就相当于是三个1的与运算，那右边这个整体运算结果是1好，最后这两个与运算再进行一个或运算，0或1应该是等于1，所以基于刚才给出的这个加法，我们用这个逻辑判断就可以得到V的最终结果，是等于1此时表示是有溢出发生的，那第2个式子逻辑运算夸考同学也可以自己带进去验证一下，所以同样可以得到一当有意初发生的时候，也就是V=1的时候，一定是左边这个部分运算的结果等于1或者右边这个部分运算的结果等于一。右边这个部分运算的结果等于1，那当加数和被加数的符号位都为1最终运算的结果，符号位为0的时候，就会导致左半部分预算结果为一，而如果加数和被加数符号位都为0，最终运算的结果符号位为1，此时就会导致右半部分的运算，结果为1，其实这个是字背后的逻辑，依然是我们之前提到过的东西，如果两个复数附加附最终等于挣，那么这种情况下是有溢出的，如果张家城等于负此时也是有溢出的，那既然背后的逻辑这么简单，我们为什么还要折腾写出这么复杂的一个逻辑表达式呢？原因是这样的于霍飞这些逻辑运算可以很方便的用一个门电路就实现与门或门联盟，就是分别实现我非的只要我们写出来我们已经把这个地方这么多其实我们。相当于我们已经把啊硬件的电路都给设计好了好，所以这个地方折腾这么多，其实我们就是在设计硬件电路的实现，只不过我们是用数学表达式的方式把它表示出来而已好的，这是硬件判断溢出的第1种方法，接下来看第2种是情况同样只采用一位符号位，但是我们会根据数据位的敬畏情况，还有符号位的进位情况来进行溢出的判断，当符号位的进位为0，然后最高数值位的进位为1的时候，此时发生了上亿儿铺好被精锐，唯一最高数值为敬畏为0的时候，说明此时发生了下一好我们来解释一下什么叫符号位的进位和数值位的进位，同样的我们结合这给出的例子好，现在计算a和C补码相加的一个值啊，末位1+0=11+0=11+1=0，向高位进一个1那1+1再加，1=1向高位进一个1一加一等于零高位进一个一一加一等于零。+0=11+0=11+1=0，向高位进一个1那1+1再+1=1向高位进一个11+1=0，向高位进一个1 1+1=0，向高位再进一个1好，现在我们已经算到了树职位的最高一个为这个为等于0，嘉羿在嘉羿，那么应该是=0，然后往高位进一个1，这就是所谓最高数值位的进位，这儿是进了一个一好，接下来是符号位的运算，0+0再加1应该是等于1，那上小学说我们是不是提到过近卫卫的一个问题，当a和C相家的时候，近卫卫应该是等于0，也就是这所谓号位向更高位产生了一个进位CS，好，所以在这个例子当中CS=0，然后CE=1此时一定是发生了上亿，那第2个例子，大家也可以验证一下这两个数相加最高数值位的进位符号位的经纬应该。那第2个例子大家也可以验证一下，这两个数相加，最高数值位的进位应该是0，然后符号位往更高位的进位应该是一两个负数相加，最终得到的结果是一个正数，而原本的符号位往更高位又进了一个1，此时说明发生了夏季好，所以只要发生了一出，那么刚才我们提到的这两个V的数值肯定是不同的，那怎么用硬件来判断不同的逻辑呢？只需要用我们之前提到的异或运算就可以，计算机硬件只需要把符号辈的敬备和最高数值为的敬畏进行一个异或运算，如果异或的结果为0，那么表示没有艺术，抑或的结果，为一则表示有意出，因为之前我们说过抑或的逻辑就是如果两个逻辑是不一样，那么以后的结果为1，而如果两个逻辑是相同的异或的结果，都是您这样的话，就符合之前我们给出的判断逻辑好，那这是用硬件判断溢出的第2种方法最后一种。溢出的第2种方法好再看，最后一种用硬件判断溢出的方法，我们可以采用双符号位的补码来表示，一个数正数的符号位是两个0，负数的符号位是两个一之前我们介绍的补码都只有一个符号位，现在我们把符号位进行一个拓展，让它有两个符号位，并且两个符号位一定是00或者11好，我们来试一下，用双符号位表示的a和C进行一个相加的操作，当然的两个符号位都会参与我们的加法运算，同样要考虑进位这个问题，那最终得到的结果是这样子，也就是运算结果的两个符号位一个为0，一个为一，此时我们可以断定是发生了上亿，而第2个例子，两个复数用双符号位补码的形式来表示相加之后啊，最终得到的结果符号位为1和零两个符号呗不一样，那么此时说明发生了下一在最终结果表示的是本来应该得到的正确的一个复姓表示的。符号a表示的是实际得到的一个正负的结果，所以本应得到正的而实际得到了负的，那此时一定是上亿本应得到负的，但是运算的结果，是一个正的，此时可以判断发生了下意识好，所以如果要用硬件来判断溢出的话，烦恼我们只需要用一个异或运算把运算结果的两个符号位进行，一个异或如果异或的结果为0，也就是两个符号位都相同，那么说明没有溢出一会结果为一说明有溢出，那这给出的是一个有溢出的情况啊，大家也可以结合之前的例子来自己动手验证一下啊，如果说没有发生溢出的话，那最终得到的两个符号位一定是相同的，这儿就不再赘述好，那我们还需要补充一个关于双符号位补码的，呃一些一些边角的知识点双符号被补满，又称为模似不满，而之前我们学习的单符耗费的那种不慢，又称为摩尔不慢如果把这个逗号把它看作是小数点的话那么他前边这一位的。前面这一个应该是2的一次方，那如果再往前还有一位的话，应该是2的二次方也就是4，而之前我们简单的介绍过模运算，不过模4的话其实是相当于啊位全小于4的这些部分给保留而位权大于4的这些部分全部把它舍弃，所以如果把这个地方看作是小数点的话，那由于我们只保留小数点前边的两倍，所以这就相当于计算机在运算之后进行了一个模式的操作，那单符号被被称为摩尔补码的原因也是类似的，如果把这个地方看作是一个小数点，那么他前面这一位的位权就应该是2的0次方在前边，如果还有别的味，那应该是2.1次方，那魔2就相当于把卫泉小于2的这些部分给保留而位权大于或者等于2的啊，这些部分全部给舍弃最大这两个主意那另外一点需要补充的是虽然我们这儿看到的这个符号为但是其实这种不满。这两个概念需要注意好，那另外一点需要补充的是，虽然我们这儿看到的这个补码，它有两个符号位，但是其实这种补码在内存里在计算机当中进行存储，实际也只存储一个符号位，只不过在这个补码进行运算之前，在运算之前会复制一个符号位，然后接下来补码的运算会让两个符号位同时参与运算，所以这种双负号位的补码并不会增加存储所需要的空间好的，那这就是关于溢出判断的三种方法，其中最后这种方法是最常好的，但无论是哪种方法，其实背后的核心逻辑都是两个同号的数相加，最终得到了一个1号的结果，此时一定是发生了移出，那么发生溢出的时候，其实是说明我们给定的这个机器字长这个源码补码的位数足够表示那么大的范围，那如何让原码补码表示更大范围的数，从而避免溢出的发生呢一个最容易想到的办法就是我们可以让。最容易想到的办法就是我们可以让短数据把它拓展为常数句，比如大家编程的时候应该遇到过把印制行扩展为浪形这样的情况，那么在这种短数据拖出来长数据的时候多出来的那些为应该怎么填补呢？比如短数据本来只占一个字节，那我们把拓展为两个字节的长数据，那多出来的那8个比特币应该如何填充，这就是所谓的符号扩展的问题，好来看一下吧，为扩展为16位，那对于正整数来说，由于原码反码补码的表示都一样，所以8位扩展为16倍的时候，我们只需要在符号费还有啊之前的这个数值位之间中间把它填上8个0就可以，然后再来看负整数的拓展，负数的原码反码补码表示是不一样的，那么源码的复述扩展起来很方便，同样我们只需要在符号位和数值为中间的部分补上新的8个0由于复苏的方法和他的数字部分都是相反的我们辛苦的这些由于复苏的方法和他的数字部分都是相反的我们辛苦的这些费用。就可以，那对于砝码来说，由于负数的砝码和源码，它的数值部分都是相反的，所以我们新补的这些V应该刚好和源码相反，源码补零我们就需要补一好最后再看平码补码的，这个补位规则和反码是一致的，同样都是天意，因为上一小节我们说过不买房，码原码之间有这样的规律，我们找到补码，从右往左看的第1个一然后再画一条线，这条线的左边的数值部分和反码应该是保持一致的，所以左边这些新鲜的味砝码怎么做，那补码就应该怎么做，因此和砝码一样都是天一好，这是定点整数的符号扩展，接下来再看定点小数的一个符号扩展，对于正的小数来说，同样的原码反码补码表示都是一样的，只不过当我们把8位的小数拓展为16位的小数的时候由于小数点是固定在这个符号v后边这个位置而每一味的为全市根据各个费和这小树点的相对位置关系确定了因此为了保证。来确定当中，因此为了保证每一个为了位权不变，也就是拓展之后整体的数值不变，所以我们只能在尾部添加新的那些位，对于正数来说，我们只需要补0就可以好再看负数对于源码表示的附小书啊，我们只需要在末尾添0就可以而砝码表示的附小数，我们需要把这些新鲜的V全部设为一好，最后是不嘛，我们需要在末位全部签名，那么原因还是一样的啊，从右往左看找到卓玛的第1个1，然后这样画一条线，它的这个一还有他的右半部分需要保持和原码一致，然后这条线的左边又需要和砝码保持一致，那由于我们要宣布的是右边的这些低位，所以原码怎么做，不卖就跟着怎么做好的，那这就是定点小数的一个符号扩展的问题变成传述橘汁后所表示的数值范围还要数职的精度都会有所扩展这种策略就可以在一定程度上避免溢出。好的，那这就是定点小数的一个符号扩展的问题，把短数据变成长数据之后啊，所能表示的数值范围还有数值的精度都会有所扩展，那用这种策略就可以在一定程度上避免溢出这种情况的发生，好的，那这个学校的内容比较多，比较杂，我们介绍了定点数的加减运算，怎么实现对圆满的加减运算的实现啊，相对来说会复杂一些，所以实际当中通常使用补码的方式来实现啊，加法或者减法，那对于补码的减法操作，最终我们肯定可以把它变为等价的加法操作，并且最后符号位会参与运算符号位，也要考虑到经费相关的问题，那对补码进行加法运算有可能会导致溢出的问题，如果两个同号的数相加，最终得到的结果符号改变了，那么就说明发生了一出超出补马政数所能表示的范围，这种现象称为上一超出补码付数所能表示的范围，这种现象称为夏一衲，我们介绍了三种用硬件判断溢出的方法，其中第3种方法是阿。啊，更重要的也就是双符号位的这种方法，那在接受双符号位的时候，我们也引出了两个概念叫做模四不骂和模二不骂，这两个概念大家也需要注意，最后为了解决溢出，我们介绍了符号扩展相关的问题比较容易错的是对于负数补码的一个呃扩展问题，那今年整数和小数的扩展啊策略都会不太一样，那这就不再赘述好了，那以上就是这小节。