变色龙算法chameleon聚类

参考论文：
CHAMELEON A hierarchical clustering algorithm using dynamic modeling
chamelon算法是一种层次聚类算法。

一、层次聚类

层次聚类算法的关键是如何判定两个子簇是最相似的。
度量两个子簇相似性的常见方法有：

单连接规则就是用两个子簇中最近的一对点之间的距离来刻画这两个簇的相似性。基于这种度量方法的聚类容易受异常点、噪音的影响。

二、closeness和inter-connectivity

1.closeness的介绍

关于下图(a),(b),( c ),(d)，如果聚类算法只侧重于两个子簇之间的近邻节点的靠近程度，则将合并(a) 和（b）。事实上，（c）和（d）是属于同一个簇。因为（c）和（d）簇之间的距离与它们簇内个元素的距离几乎相近，所以（c）和（d）是同构的。

同样的，对于下图中的(a),(b),(c ),(d)，如果算法只侧重于两个子簇之间的近邻节点的靠近程度，则将合并© 和（d）。

这里我们将两个簇之间的近邻节点的靠近程度称为“紧性”（closeness）。

2.inter-connectivity 的介绍

关于下图(a),(b),(c ),(d)，如果聚类算法只侧重于两个子簇之间的邻接区域的大小，则会选择合并（c）和（d）。而实际上，（a）和（b）是同构的。

同样的，对于下图中的(a),(b),(c )，如果算法只侧重于两个子簇之间的邻接区域的大小，则将合并(a) 和（c）。

这里我们将两个簇之间的邻接区域的大小称为“互连接性”（inter-connectivity ）。

为了能使算法对上面四幅图中的子簇进行正确的合并，算法必须在聚类的时候既考虑到closeness，又考虑到inter-connectivity 。而且每一对簇之间的closeness和inter-connectivity的度量需要结合这一对簇自身的结构特点，即由绝对指标The absolute closeness 和The absolute inter-connectivity转化为相对指标the Relative closeness和the Relative Inter-Connectivity。chameleon算法满足上述要求。

三、chameleon算法

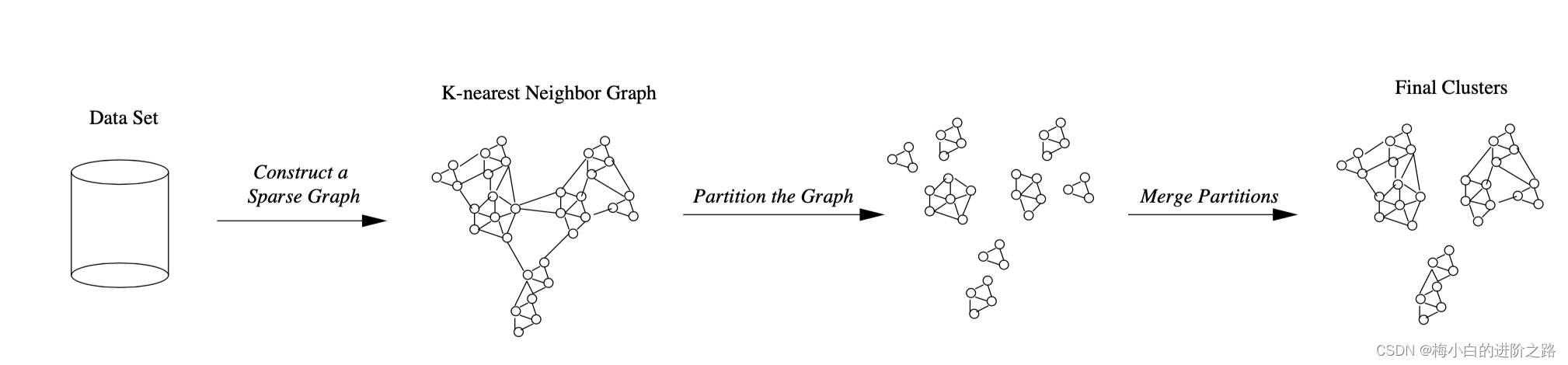
chameleon算法是一个两阶段算法。

第一阶段：找到初始子簇

第一阶段是用k-近邻算法将数据集构建成一个图。将数据集中的每一个点和它k-近邻的点连接起来。每一条线段对应一个权重，这个权重是由这条线段所连接的两个点的距离的倒数来表示。边的权重代表相似度。两点距离越大，连接两点的边的权重越小，两点的相似度越低。

采用图分割技术对由k-近邻构建的图进行分割。分割的标准是连接不同区域的边的权重最小化。边的权重越小， 两点之间的距离越大，两点的相似度越低。所以连接不同区域的边的权重最小意味着不同区域的点相似度越低。

图分割工具为metis。python可安装metis库。具体分割流程为：依据连接不同区域的边的权重和最小的原理，将原k-近邻图分成两部分，要求这两部分各自至少含原图的25%的点，这是因为如果子区域点点太少，无法计算the Relative closeness和the Relative Inter-Connectivity。对较大部分区域再进行划分，直到所得到的较大部分区域所包含的点的个数少于预先给定的值（MinSize）。MinSize值要适中，通常将MinSize的值设置在整体数据集的1%～5%之间。

第二阶段：动态合并子簇

首先给出the Relative closeness和the Relative Inter-Connectivity的定义。

1.the Relative Inter-Connectivity的公式

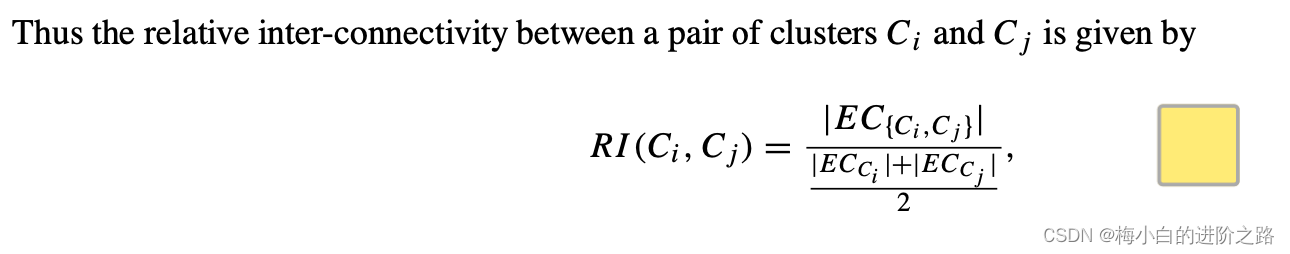
其中 E C { C i , C j } EC_{\{C_i,C_j\}} EC{Ci​,Cj​}​是指$C_i$和$C_j$相连接的边的权重的和。
$E{C}_{C_i}$是指属于$C_i$内的边的权重的和。

2.the Relative closeness的公式

其中 S ‾ E C { C i , C j } \overline{S}_{EC_{\{C_i,C_j\}}} SEC{Ci​,Cj​}​​是指$C_i$和$C_j$相连接的边的平均权重。
${\overline{S}}_{E{C}_{C_i}}$是指属于$C_i$内的边的平均权重。

3.构造函数

因为要求the Relative closeness和the Relative Inter-Connectivity都很大时，才合并相应的两个子簇。为了避免遍历所有子簇的the Relative closeness和the Relative Inter-Connectivity，构造一个关于
the Relative closeness和the Relative Inter-Connectivity的函数，通过函数值来判断是否合并两个簇。


合并使上述式子最大化的两个子簇。