堆排序中 i 位置的节点的子节点位置为 2i+1, 2i+2, 父节点为 (i-1) / 2

在堆排序中使用到了左右子节点，它们的节点位置是 2i + 1 和 2i + 2,下面是如何得到这个结论：

1.我们首先假设一个节点：它的数组下标是 i ，在二叉树的第 n 层的第 x + 1 个

我们可以知道完全二叉树的前 n 层的总结点数是 2 ^ n - 1 个，在第n层的节点，前n-1层有 2^(n-1) - 1 个节点，加上他本层前面的x个节点，则：

 i = 2^(n-1) - 1 + x

2.我们再来看子节点，i 的子节点在第 n + 1 层，对于左子节点，令他在数组中下标为 j。
左子节点在n+1层中，前面应该有2x个节点，（因为i在第n层前面有x个，每一个节点在下一层都会有2个节点）。

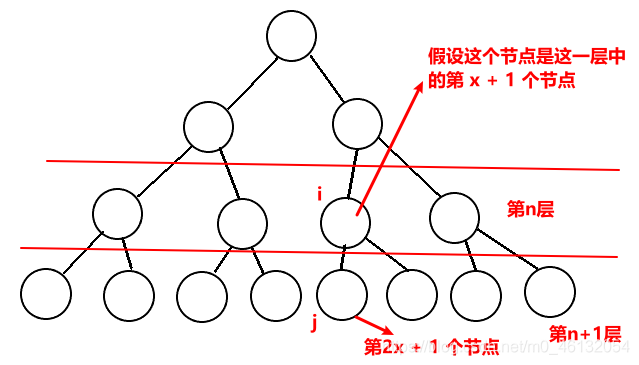
所以得到

j = (2^n - 1) + 2x = 2(2^(n-1) + x -1) + 1 = 2i + 1

这样左节点下标 j = 2i+1，右节点也就是 2i+2。

3.再来分析父节点为什么是 (i - 1) / 2

i 的父节点在第 n - 1 层，对于父节点，令他在数组中下标为 k。

因为 i = 2^(n-1) - 1 + x
得到 i + 1 = 2^(n-1) + x

k = 2^(n-2) - 1 + x/2 
  = 2^(n-1)/2 + x/2 -1 
  = (2^(n-1) + x)/2 -1
  = (i-1)/2