数据结构与算法（python版）

最近学习数据结构，对于从未接触过数据结构的我来说，老师不仅讲解理论，还有代码的逐层分析，非常不错，受益匪浅！！！（以下是学习记录）

黑马程序员孔德海老师教程

重点+基础语法

1. python语言只要是给出的变量名，里边存储的都是地址值(可以把类，函数，付给变量a)。
   如a=5 a=“s” a=Person() a=f 方法

java基本数据类型中，变量a存放的是数值。引用数据类型(对象，数组，集合)的变量a存放的是地址。

#1
strat=time.time()

时间复杂度(主要关注最坏时间复杂度)

不同方法间的复杂度

import time
start= time.time()
for i in range(0,1001):
    for j in range(0,1001):
        for k in range(0,1001):
            if i+j+k==1000 and i**2+j**2==k**2:
                print(i,j,k)
end = time.time()
print("总开销：",end-start)#总开销： 126.49699997901917

start1= time.time()
for i in range(0,1001):
    for j in range(0,1001):
        k=1000-i-j
        if i**2+j**2==k**2:
            print(i,j,k)
end1= time.time()
print("总开销：",end1-start1)#总开销： 1.0120000839233398

1. T(n)时间复杂度，n执行的步数
   大O表示法，只记录最显著特征O(n)=nxn
   
2. 最坏时间复杂度（平常说的就是这个）
   比如对一个list排序，无序的复杂度要高于有序

基本步骤：顺序，条件(取T最大值)，循环
li.append()不能看成一步，只有分析函数中的封装才能看到append的时间复杂度

time.it，list，dic内置函数

from timeit import Timer
def test3():
   l = [i for i in range(1000)]
t3 = Timer("test3()", "from __main__ import test3")#1函数名，2import，因为这个Timer不一定在这里运行
print("comprehension ",t3.timeit(number=10000), "seconds")#test3()执行10000次后，10000次总的执行时间

import time
start=time.time()#从1970年到现在的计时秒数
end=time.time()-start#返回秒

对于上例使用不同方法实现时

1.
('list(range(1000)) ', 0.014147043228149414, 'seconds')
('l = [i for i in range(1000)]', 0.05671119689941406, 'seconds')
('li.append ', 0.13796091079711914, 'seconds')
('concat加 ', 1.7890608310699463, 'seconds')
2.由于数据的存储方式不同，导致插头部和尾部
append()#2.159s
insert(0,i)#30.00s
pop(end)#0.00023,对尾部弹出
pop(0)#1.91

数据结构

数据是一个抽象的概念，将其分类后得到程序语言的基本类型，如int,float,char。数据结构指对数据的一种封装组成，如高级数据结构list，字典。数据结构就是一个类的概念，数据结构有顺序表、链表、栈、队列、树。

算法复杂度只考虑的是运行的步骤，数据结构要与数据打交道。数据保存的方式不同决定了算法复杂度

程序 = 数据结构 + 算法
总结：算法是为了解决实际问题而设计的，数据结构是算法需要处理的问题载体

抽象数据类型(Abstract Data Type)
抽象数据类型(ADT)的含义是指一个数学模型以及定义在此数学模型上的一组操作。

== 代码编写注意==

2.对于链表要先接入新的node，再打断原来的，要注意顺序

下面讲的各种表都是一种数据的封装结构

顺序表

顺序表+链表=线性表：一根线串起来，两种表都是用来存数据的

顺序表的2个形式

1. 计算机存储
   计算机最小寻址单位是1字节，就是一个字节，才有一个地址，所有的地址都是统一大小0x27 4个字节
   
2. 元素内置顺序表
   对于存放一个含有相同类型元素的list来讲，用顺序表封装成一个数据结构。
   
   
3. 元素外置顺序表
   
   元素内置顺序表，是指存储的数据类型都是一样，这样为每个元素开辟的空间都是一样大的，在根据index找元素的时候
   如list1=[1,2,3], 可以根据list的首地址0x12，很容易计算要查询元素的物理地址=0x12+index x 4.
   元素外置, 指存的数据类型不一样，如list2=[1,3,“b”,4,“ccc”]
   

顺序表的结构与实现

对于python来讲已经做好封装，不需要写容量，元素个数


so常用的是分离式

顺序表数据区扩充

如果数据要来回增，删，导致空间不稳定，所以有了策略

顺序表的操作

python_list使用顺序表数据结构

1.表头与数据分离式 2.因为一个list中有int，也有字符所以用的是元素外置 3.动态顺序中的倍数扩充

链表

# cur做判断，逻辑(不是指针)走到最后一个元素时，里面的方法体是执行的
# 用cur.next做判断，while循环中是不执行的
# 如果发现少一次执行语句，可以手动打印，就不用完全在while循环中执行

java，c语言是需要中间变量temp，才能完成交换，只有python可以直接交换

单链表的实现

cur：指针地址
cur.elment:地址中的元素
cur=self._head先提出等式右边地址，再给cur

多写几次单链表，有助理解，链表的运行过程

1. """单链表的结点，里面存放element区和next"""相当于元祖（element，next）
class SingleNode(object):
    def __init__(self,item):
        # _item存放数据元素
        self.item = item
        # _next是下一个节点的标识
        self.next = None
2."""单链表数据结构类，具有以下功能"""相当于python中的list数据结构类，同时它也具有以下功能
class SingleLinkList(object):
    """存放一个属性P，好用来指向第一个节点"""
    def __init__(self，):
        self._head = None# _ 私有属性,head=None说明P指向的单链表中没有node

    def is_empty(self):
        """判断链表是否为空"""
        return self._head == None

    def length(self):
        """链表长度"""
        # current游标用来遍历节点，初始时指向头节点
        cur = self._head#直接指到第一个节点
        count = 0
        # 尾节点指向None，当未到达尾部时
        while cur != None:
            count += 1
            # 将cur后移一个节点
            cur = cur.next #相当于指向下一个节点
        return count

    def travel(self):
        """遍历链表"""
        cur = self._head#直接指到第一个节点
        while cur != None:
            print cur.item,#打印第一个节点
            cur = cur.next#相当于指向下一个节点
        print ""
    
       def add(self, item):
        """头部添加元素"""
        # 先创建一个保存item值的节点
        node = SingleNode(item)
        # 将新节点的链接域next指向头节点，即_head指向的位置,有先后，否则会丢失链
        node.next = self._head
        # 将链表的头_head指向新节点
        self._head = node
        
    def append(self, item):
        """尾部添加元素"""
        node = SingleNode(item)
        # 先判断链表是否为空，若是空链表，则将_head指向新节点
        if self.is_empty():
            self._head = node#append时候，我只要保证把我的node地址给你就行，node.next不用管
        # 若不为空，则找到尾部，将尾节点的next指向新节点
        else:
            cur = self._head
            while cur.next != None:
                cur = cur.next
            cur.next = node#直接将node送给cur.next，内部操作就是把node结点地址给他

if __name__=="__main__":
    li=SingleLinkList()
    print(li.is_empty())
    print(li.length())
    node = SingleNode(3)
    li.append(11111)
    li.travel()
  
  3.使用
   node =Node(100)
   single_obj=SingleLinkList(node)#创建node，让单链表指向它
   single_obj=SingleLinkList()#直接创建空链表

指定位置添加元素


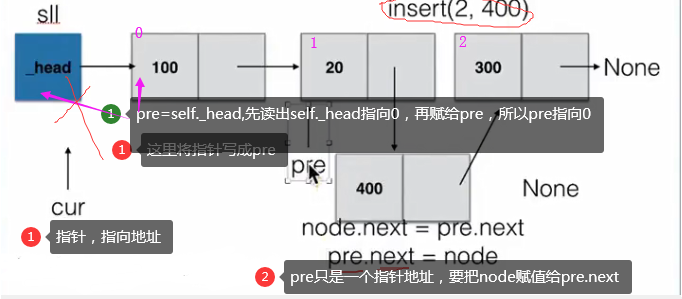
    def insert(self, pos, item):
        """指定位置添加元素"""
        # 若指定位置pos为第一个元素之前，则执行头部插入
        if pos <= 0:
            self.add(item)
        # 若指定位置超过链表尾部，则执行尾部插入
        elif pos > (self.length()-1):
            self.append(item)
        # 找到指定位置
        else:
            node = SingleNode(item)
            count = 0
            # pre用来指向指定位置pos的前一个位置pos-1，初始从头节点开始移动到指定位置
            pre = self._head
            while count < (pos-1):
                count += 1
                pre = pre.next
            # 先将新节点node的next指向插入位置的节点
            node.next = pre.next
            # 将插入位置的前一个节点的next指向新节点
            pre.next = node

查找节点是否存在

def search(self,item):
        """链表查找节点是否存在，并返回True或者False"""
        cur = self._head
        while cur != None:#一直往后走，起到遇到none停止
            if cur.item == item:
                return True
            cur = cur.next
        return False

删除节点

def remove(self,item):
        """删除节点"""
        cur = self._head
        pre = None
        while cur != None:
            # 找到了指定元素
            if cur.item == item:
                # 如果第一个就是删除的节点
                if not pre:
                    # 将头指针指向头节点的后一个节点
                    self._head = cur.next
                else:
                    # 将删除位置前一个节点的next指向删除位置的后一个节点
                    pre.next = cur.next
                break
            else:
                # 继续按链表后移节点
                pre = cur
                cur = cur.next

链表与顺序表的对比

链表只能记录头节点地址，因此在访问，尾部插，中间查时，都需要从头节点，遍历过去，所以复杂度O(n)

1. 链表可以利用离散的空间，顺序表只能开辟完整的连续空间，只要list不够，必须重新开辟
2. 链表时间花费到遍历地址上，顺序表花费到表的复制搬迁
   

双向链表

对于前面单向的，当前node不能查看其前面node的信息，所以引入双向。添加，删除node时，要保证每个node中的P,N都 给上值，如：中间插入

头部插入元素

def add(self, item):
        """头部插入元素"""
        node = Node(item)
        if self.is_empty():
            # 如果是空链表，将_head指向node
            self._head = node
        else:
            # 将node的next指向_head的头节点
            node.next = self._head
            # 将_head的头节点的prev指向node
            self._head.prev = node
            # 将_head 指向node
            self._head = node

尾部插入元素

def append(self, item):
        """尾部插入元素"""
        node = Node(item)
        if self.is_empty():
            # 如果是空链表，将_head指向node
            self._head = node
        else:
            # 移动到链表尾部
            cur = self._head
            while cur.next != None:
                cur = cur.next
            # 将尾节点cur的next指向node
            cur.next = node
            # 将node的prev指向cur
            node.prev = cur

中间插入

单向循环链表

由于是循环列表，最后的尾结点不再是None结束，而是指向self._head
由于一开始将cur = self._head设成游标，所以判断语句只能是cur.next
while cur.next != self._head
使用cur.next不能进到循环体，会导致少一次打印，可以手动打印

length(self)返回链表长度

def length(self):
        """返回链表的长度"""
        # 如果链表为空，返回长度0
        if self.is_empty():
            return 0
        count = 1
        cur = self._head#指针启动地址
        while cur.next != self._head:#因为循环链表最后一个node要带有self._head，所以通过判断是否有self._head来看是否一个循环结束
            count += 1
            cur = cur.next
        return count

头部添加节点

def add(self, item):
        """头部添加节点"""
        node = Node(item)
        if self.is_empty():
            self._head = node
            node.next = self._head
        else:
            #添加的节点指向_head
            node.next = self._head
            # 移到链表尾部，将尾部节点的next指向node
            cur = self._head
            while cur.next != self._head:
                cur = cur.next
            cur.next = node
            #_head指向添加node的
            self._head = node

栈

栈=杯
顺序表，链表是用来存数据的
栈和队列不考虑数据是如何存放的，栈stack，队列是一种容器，执行什么样的操作，抽象结构。
6*（2+3）

#利用前面封装好的顺序表的二次开发
class Stack(object):
    """栈"""
    def __init__(self):#初始化的时候要生成一个容器，顺序表就是python中的list，然后再执行操作，可将list设成私有的，self.__items = []这样就不能修改原来的list容器
         self.items = []

    def is_empty(self):
        """判断是否为空"""
        return self.items == []#右边是一个判断返回True
        
#对于存放的数据结构是顺序表来讲，尾部压栈出栈复杂度为o（1），对于链表来讲，头部复杂度为o（1），所以要考虑
    def push(self, item):#从尾部压，从尾部取
        """加入元素"""
        self.items.append(item)

    def pop(self):
        """弹出元素"""
        return self.items.pop()

    def peek(self):
        """返回栈顶元素"""
        return self.items[len(self.items)-1]

    def size(self):
        """返回栈的大小"""
        return len(self.items)

if __name__ == "__main__":
    stack = Stack()
    stack.push("hello")
    stack.push("world")
    stack.push("itcast")
    print stack.size()
    print stack.peek()
    print stack.pop()
    print stack.pop()
    print stack.pop()

队列

#因为出入队总有一个复杂度为N,所以考虑是出队用的多，还是入队多，再写程序
class Queue(object):
    """队列"""
    def __init__(self):#空列表保存队列
        self.items = []

    def is_empty(self):
        return self.items == []

    def enqueue(self, item):
        """进队列"""
        self.items.insert(0,item)

    def dequeue(self):
        """出队列"""
        return self.items.pop()

    def size(self):
        """返回大小"""
        return len(self.items)

if __name__ == "__main__":
    q = Queue()
    q.enqueue("hello")
    q.enqueue("world")
    q.enqueue("itcast")
    print q.size()
    print q.dequeue()
    print q.dequeue()
    print q.dequeue()

双端队列
两个栈尾部放一起

是上面的扩展，含有的函数功能更多了

排序

排序算法的稳定性

冒泡排序O(n2)稳定

#可以将这个算法操作在顺序表上（改变存储位置），也可以操作在链表上（改变node节点）
#不论list是什么要，O（n）=n^2
def bubble_sort(alist):
    for j in range(len(alist)-1,0,-1):#n-1,n-2,,,1
        # j表示每次遍历需要比较的次数，是逐渐减小的
        for i in range(j):
            if alist[i] > alist[i+1]:
                alist[i], alist[i+1] = alist[i+1], alist[i]

li = [54,26,93,17,77,31,44,55,20]
bubble_sort(li)
print(li)

#加个检测是否交换的优化的count,这样复杂度为n
#[1,2,3,4,5,9,8]
def bubble_sort(alist):
    for j in range(len(alist)-1,0,-1):#n-1,n-2,,,1
        # j表示每次遍历需要比较的次数，是逐渐减小的
        count=0
        for i in range(j):
            if alist[i] > alist[i+1]:
                alist[i], alist[i+1] = alist[i+1], alist[i]
                count+=1
        if 0 == count:
            contine
li = [54,26,93,17,77,31,44,55,20]
bubble_sort(li)
print(li)

冒泡是稳定的

选择排序O(n2)不稳定

比如[5,5,2],就是不稳定的
选择排序，插入排序，希尔排序是把序列分成两部分，把其中的一部分元素往另外一部分做

list=[54,226,93,17,77,31,44,55,21]
def selec_sort(list):
    for j in range(len(list)-1):
        min=list[j]
        for i in range(j+1,len(list)):
            if list[i]<min:
                min=list[i]
                list[j],list[i]=list[i],list[j]

    print(list)
selec_sort(list)

插入排序O(n2)稳定

#这个想法像选择排序，每次对比选出最大，没有插序的相邻之间对比，向前移
list=[54,226,93,17,77,44,4,55,21]
    #0,   1,  2,  3  4, 5, 6 ,7, 8
def insert_sort(list):
    for j in range(1,len(list)):
        max=list[j]
        for i in range(0,len(list)-1,1):#先写第一个循化，可以直接用下表list[1],然后再加上外循环，看看j与list[1]下标的关系
            if list[i]>max:
                max=list[i]
                list[j],list[i]=list[i],list[j]
    print(list)
insert_sort(list)

#version1插序的相邻之间对比，向前移，用下面的方法
def insert_sort(alist):
    # 从第二个位置，即下标为1的元素开始向前插入
    for i in range(1, len(alist)):
        # 从第i个元素开始向前比较，如果小于前一个元素，交换位置
        for j in range(i, 0, -1):
            if alist[j] < alist[j-1]:
                alist[j], alist[j-1] = alist[j-1], alist[j]

alist = [54,26,93,17,77,31,44,55,20]
insert_sort(alist)
print(alist)

#version2
#对于上面的用for j in range(i, 0, -1):来控制i，与i-1，i-2的比较，操作比较复杂
#这里用 while i>0: i-=1 来控制指针向0的方向移动，随着i的变动，每次只比较i与i-1
def insert_sort(alist):
    # 从第二个位置，即下标为1的元素开始向前插入
    for i in range(1, len(alist)):
        # 从第i个元素开始向前比较，如果小于前一个元素，交换位置
        while i>0:
            if alist[i] < alist[i-1]:
                alist[i], alist[i-1] = alist[i-1], alist[i]
                i-=1
            else:
                break
alist = [54,26,93,1711,77,31,44,55,20]
insert_sort(alist)
print(alist)

希尔排序

def shell_sort(list):
    n=len(list)
    gap=n//2 #gap=4

    while gap>=1:#gap一直变化到1
        for j in range(gap,n):#for控制的是gap=4时的4个子序列
            i=j
            while i >0:#跟之前插入排序一样，对于一个序列的具体操作，与普通插入的区别就是gap步长
                if list[i]<list[i-gap]:
                    list[i],list[i-gap]=list[i-gap],list[i]
                    i-=gap
                else:
                    break
        gap//=2#gap减半

list = [54,26,93,17,77,31,44,55,20]
shell_sort(list)
print(list)

快速排序(不稳定)

快速排序（英语：Quicksort），又称划分交换排序（partition-exchange sort），通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
注意
1.version2 中，两个while有一个是等号，保证相同大小的元素放到mid的同一边，这是快排设计的一个思想
用version2的思想写代码

def quick_sort(alist, start, end):
    """快速排序"""

    # 递归的退出条件
    if start >= end:
        return

    # 设定起始元素为要寻找位置的基准元素
    mid = alist[start]

    # low为序列左边的由左向右移动的游标
    low = start

    # high为序列右边的由右向左移动的游标
    high = end

    while low < high:
        # 如果low与high未重合，high指向的元素不比基准元素小，则high向左移动
        while low < high and alist[high] >= mid:#加=号表示将2个一样的值放到一边，不加的话，最终迭代后也会正确
            high -= 1
        # 将high指向的元素放到low的位置上
        alist[low] = alist[high]

        # 如果low与high未重合，low指向的元素比基准元素小，则low向右移动
        while low < high and alist[low] < mid:
            low += 1
        # 将low指向的元素放到high的位置上
        alist[high] = alist[low]

    # 退出循环后，low与high重合，此时所指位置为基准元素的正确位置
    # 将基准元素放到该位置
    alist[low] = mid

    # 对基准元素左边的子序列进行快速排序
    quick_sort(alist, start, low-1)#这里要保证使用同一个list，这样产生的多个子序列下标是保持不变的，才能恢复成一个list

    # 对基准元素右边的子序列进行快速排序
    quick_sort(alist, low+1, end)


alist = [54,26,93,17,77,31,44,55,20]
quick_sort(alist,0,len(alist)-1)
print(alist)

归并排序

def merge_sort(alist):
    if len(alist) <= 1:#递归的终止条件 
        return alist
    # 二分分解
    num = len(alist)/2
    left = merge_sort(alist[:num]) 
    right = merge_sort(alist[num:])
    # 合并
    return merge(left,right)

def merge(left, right):
    '''合并操作，将两个有序数组left[]和right[]合并成一个大的有序数组'''
    #left与right的下标指针
    l, r = 0, 0
    result = []
    while l<len(left) and r<len(right):
        if left[l] < right[r]:
            result.append(left[l])
            l += 1
        else:
            result.append(right[r])
            r += 1
    result += left[l:]#当上面的while循环出来时，一个list的元素是取完的，保证将另外一个list余下的元素append
    result += right[r:]
    return result#是一个新list，不再使用之前list下标

alist = [54,26,93,17,77,31,44,55,20]
sorted_alist = mergeSort(alist)
print(sorted_alist)

递归时要注意缩进，这样可以帮助理解

排序算法效率比较

搜索

二分法
前提，二分查找只能作用于有序列表

递归法：当list处理后得到的list，还想再进行同样的操作，使用递归，但是不能无限递归下去，所以终止条件很重要，在这个例子中，要么alist[midpoint]=item，return True，要么 if len(alist) = 0: return False，用来退出递归

#递归法，每次生成一个新的list
def binary_search(alist, item):
    if len(alist) == 0:
        return False
    else:
        midpoint = len(alist)//2
        if alist[midpoint]==item:
          return True
        else:
          if item<alist[midpoint]:
            return binary_search(alist[:midpoint],item)
          else:
            return binary_search(alist[midpoint+1:],item)

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binary_search(testlist, 3))
print(binary_search(testlist, 13))

binary_search([0, 1, 2, 8, 13, 17, 19, 32, 42,],item=3)
    midpoint=4
    3<13
    binary_search([0, 1, 2, 8],item=3)
        midpoint=2
        3>2
        binary_search([8],item=3)
            midpoint=1//2=0
            3<8
                binary_search([],item=3)#a=[1,2,3,4] print(a[5:])会返回空列表
                   return False

非递归
递归法，调用函数自身,每次生成一个新的list,然后在list上操作.非递归法使用的是同一个list,所以first,last下标很重要,在while循环中,不断更新first,last值来实现对于list的取值控制

def binary_search(alist, item):
      first = 0
      last = len(alist)-1
      while first<=last:
          midpoint = (first + last)/2
          if alist[midpoint] == item:
              return True
          elif item < alist[midpoint]:
              last = midpoint-1
          else:
              first = midpoint+1
    return False
testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binary_search(testlist, 3))
print(binary_search(testlist, 13))

树

和前面的二分查找是一样的

树的存储

应用

二叉树的节点表示以及树的创建

 self.root = root#保存一个根节点,可以有,也可以没有,如果有的话说明self.root后面跟着一串数据,然后.append,在这个基础上进行加.如果self.root=None,self.root = node,为树创建第一个节点

A为第一层，2^ 0, 2^1, ,2^2
写完代码后,要分析下特殊情况是否可以跑通,若不能的话,再写特殊语句对待

广度优先的add实现的二茶树->考察队列，先入先出

#树就是链表的扩充,链表有一个element,和next,但是树有两个分支,所以lchild,rchild.
class Node(object):
    """节点类"""
    def __init__(self, elem, lchild=None, rchild=None):
        self.elem = elem
        self.lchild = lchild
        self.rchild = rchild

#树的创建,创建一个树的类，并给一个root根节点，一开始为空，随后添加节点
class Tree(object):
    """树类"""
    def __init__(self, root=None):
        self.root = root#保存一个根节点,可以有,也可以没有,如果有的话说明self.root后面跟着一串数据,然后.append,在这个基础上进行加.如果self.root=None,self.root = node,为树创建第一个节点

    def add(self, elem):#广度优先的添加方式创建的二茶树
        """为树添加节点"""
        node = Node(elem)
        #如果树是空的，则对根节点赋值,若没有这行,直接走到下面会出错
        if self.root == None:
            self.root = node
        else:
            queue = []
            queue.append(self.root)
            #对已有的节点进行层次遍历
            while queue:#          通过不断的压入队列，里面的数将会越来越多，不会为0
                #弹出队列的第一个元素
                cur = queue.pop(0)
                if cur.lchild == None:
                    cur.lchild = node
                    return
                elif cur.rchild == None:
                    cur.rchild = node
                    return
                else:
                    #如果左右子树都不为空，加入队列继续判断
                    queue.append(cur.lchild)
                    queue.append(cur.rchild)

二叉树的遍历

广度优先遍历(层次遍历)

def breadth_travel(self):
        """利用队列实现树的层次遍历"""
        if self.root == None:
            return
        queue = []
        queue.append(root)
        while queue:#这个queue最后是要为空的（上面的那么add的queue，由于满足条件就会return，所以不会空）
            node = queue.pop(0)
            print node.elem,
            if node.lchild != None:
                queue.append(node.lchild)
            if node.rchild != None:
                queue.append(node.rchild)

深度优先遍历

每次把框缩小一开始0为根节点,然后1为根节点,然后3为根节点,根节点一直变动

def preorder(self, root):
      """递归实现先序遍历"""
      if root == None:#控制迭代结束
          return
      print root.elem
      self.preorder(root.lchild)
      self.preorder(root.rchild
      
def inorder(self, root): 
      """递归实现中序遍历"""
      if root == None:
          return
      self.inorder(root.lchild)
      print root.elem
      self.inorder(root.rchild)
      
def postorder(self, root):
      """递归实现后续遍历"""
      if root == None:
          return
      self.postorder(root.lchild)
      self.postorder(root.rchild)
      print root.elem

根据数据画树图

一定要中序：用来分割数据
前、后序：用来找根

树的补充

只列出大纲，后序学习

二叉排序树（BST）

平衡二叉树（AVL）

特点：1.是二叉排序树 ⒉满足每个结点的平衡因子绝对值<=1

红黑树

红黑树是一个“适度平衡”的二叉搜索树，而非如AVL一般“严格”的平衡。（说它不严格是因为它不是严格控制左、右子树高度或节点数之差小于等于1。）
面试常问：什么是红黑树？

1.每个节点只能是红色或者黑色。
2.根节点必须是黑色。
3.红色节点的子节点只能是黑色。
4.从任一节点到其每个叶子节点，的所有路径上，包含黑色节点的数目相同。

多路查找树

B-树（多路平衡查找树）

视频增删查
B树又称为多路平衡查找树，是一种组织和维护外存文件系统非常有效的数据结构。比如数据库的索引。

B+树

b+树和b树的区别_B+树和B/B树的区别？Mysql为啥用B+树来做索引？
b+树适合范围查找，比如找年龄在18-22岁的人的信息，先用随机查找找到18，再用顺序查到到22，速度极快，这也是为啥Mysql用B+树来做索引。

主要区别：
1.所有关键字都会在在叶子节点出现
2.内部节点(非叶子节点)不存储数据（b树内部节点是存储data的），数据只在叶子节点存储（叶子节指其下没有子树了）
3.所有叶子结点构成了一个链指针，而且所有的叶子节点按照顺序排列。

B+树比B树有什么优势？
1.每一层更宽，更胖，存储的数据更多。因为B+树只存储关键字，而不存储多余data.所以B+树的每一层相比B树能存储更多节点。
2.所有的节点都会在叶子节点上出现，查询效率更稳定。因为B+树节点上没有数据，所以要查询数据就必须到叶子节点上，所以查询效率比B树稳定。而在 B 树中，非叶子节点也会存储数据，这样就会造成查询效率不稳定的情况，有时候访问到了非叶子节点就可以找到关键字，而有时需要访问到叶子节点才能找到关键字。
3.查询效率比B树高。因为B+树更矮，更胖，所以和磁盘交互的次数比B树更少，而且B+树通过底部的链表也可以完成遍历，但是B树需要找到每个节点才能遍历，所以B+树效率更高。

总结:
1.存的多 2.查询稳定 3.查的快

代码

class TreeNode:
    def __init__(self, value=0, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right



def dfs_recursive(node):
    if node is None:
        return
    print(node.value)
    dfs_recursive(node.left)
    dfs_recursive(node.right)

#处理完一个节点后将此节点的左右放到queue中，每次处理queue中的第一个
def bfs_recursive(queue):
    print(queue[0].value)
    if queue[0].left !=None:
        queue.append(queue[0].left)
    if queue[0].right != None:
        queue.append(queue[0].right)
    if len(queue)==1:
        return
    else:
        bfs_recursive(queue[1:])


# 调用递归DFS函数
if __name__ == '__main__':
    # 构建一个简单的二叉树
    root = TreeNode(3)
    root.left = TreeNode(4)
    root.right = TreeNode(8)
    root.left.left = TreeNode(9)
    root.left.right = TreeNode(10)
    root.right.left = TreeNode(11)
    #dfs_recursive(root)
    queue=[root]
    bfs_recursive(queue)