一、B-树的提出
从严格意义上讲,B-树并不是二分查找树。在物理上,B-树的每一个结点都可能包含多个分支。然而,在逻辑上将,B-树依然等效于传统的二叉搜索树。B-树的定义者,将其定义为一棵平衡的多路搜索树。
为什么要提出B-树呢?最初,B-树的提出原因就是弥合不同存储级别之间在访问速度上的巨大差异,也就是实现高效的I/O。
在现实生活中 系统存储容量的增长速度 << 应用问题规模的增长速度。在当今的世界当中,典型的数据集(数据库规模)都是以TB为单位,而我们的内存大小也大多都是8G、16G、32G、64G…。因此,相对而言,我们的内存容量非常小,并且呈现越来越小的趋势。
那么为什么不直接把内存做大一点呢?实际上,当我们的存储器容量越大/小,访问速度就会越慢/快。
事实1:不同容量的存储器,访问速度的差异悬殊。以磁盘与内存为例: m s / n s ms / ns ms/ns > > > 1 0 5 10^5 105,如果一次内存访问需要一秒,那么外存访问就相当于一天。因此,为了避免一次外存访问,我们宁愿访问内存10次、100次、甚至千次、万次。
大多数的存储系统,都是分级组织的(Caching),最常用的数据尽可能放在更高层、更小的存储器中,如果实在找不到,才向更低层、更大的存储器索取。如果希望向更低的存储级别写入,或者向更高的存储级别读出数据,我们都称之为I/O。更高层的存储器,向更低层的存储器访问都可以称为外存访问。为了避免访问速度的差异悬殊,我们要尽量避免I/O操作。
事实2:从磁盘中读写1B的数据,与读写1KB的数据几乎一样快。
因此,无论是内存向外存写入数据,还是外存向内存读出数据,涉及的数据都是批量式地以页或块为基本单位。在大量数据的访问中,我们就要充分利用批量访问的特性:要么就一次性访问1KB的数据,要么就1B也不访问。
而基于上面两个事实,我们的主角B-树就扮演了一个非常重要的角色。下图就是一个典型的B-树。
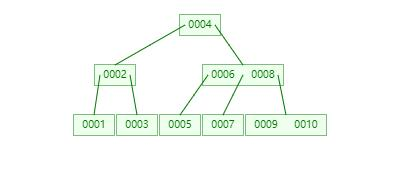
我们可以看出,B-树相对于二叉搜索树,每一个结点可以拥有更多的分支,表现的更宽、更矮。同时,所有的叶子结点都处于同一个深度。从这个意义上讲,它不失为一种理想平衡的搜索树。
在多级存储系统中使用B-树,可针对外部查找,大大减少I/O次数。
难道,我们之前学习过的AVL树还不够吗?比如,如果有 n = 1 G n=1G n=1G 个记录,也就是说使用AVL树每次查找有可能需要 l o g ( 2 , 1 0 9 ) = 30 log(2, 10^9)=30 log(2,109)=30 次I/O操作,也就是深入30层低级存储层,并且每次只能读出一个关键字,得不偿失。
那么B-树表现又如何呢?我们知道B-树每一个结点可以包含多个关键字,它可以充分利用外存对批量访问的高效支持,将此特点转换为B-树的优点。每下降一层,都是以一个多关键字的结点为单位。
那么B-树具体应该多少个关键字为一个结点呢?这需要视磁盘的外存本身设置的数据缓冲页的大小而定,假设一个页的大小为1KB,每一个关键字的大小是4B,那么一个结点就应该包含 n = 1 K B / 4 B = 250 n=1KB/4B=250 n=1KB/4B=250 个关键字。目前多数的数据库系统采用 n = 200 n=200 n=200 ~ 300 300 300 个关键字。
回到我们之前举的 1 G 1G 1G数据查询的例子,若取 n = 256 n=256 n=256,则每次查找只需要 l o g ( 256 , 1 0 9 ) ≤ 4 log(256, 10^9)≤4 log(256,109)≤4 次I/O,而4次相对于AVL树的30次,是一个非常大的提高。
二、B-树的定义
所谓 m m m 阶B-树,即 m m m 路平衡搜索树( m ≥ 2 m≥2 m≥2),这里的路,可以理解为分支。
外部结点的深度统一相等,所有叶结点的深度统一相等。
【解释】叶结点:叶结点是内部结点最后一层的结点,外部结点:外部结点是叶结点的空孩子。
B-树的树高=外部结点的高度。
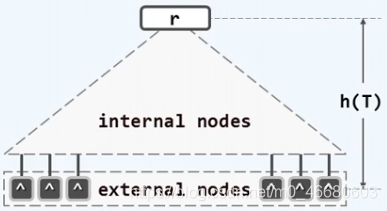
B-树的每个内部结点各有:不超过
n
=
m
−
1
n=m - 1
n=m−1 个关键字,不超过
m
m
m 个分支。
具体的,
m
m
m 阶B-树的根结点的分支数在
[
2
,
m
]
[2,m]
[2,m]之间,其余非根结点的内部结点的分支数在
[
⌈
m
2
⌉
,
m
]
[\lceil\frac{m}{2}\rceil,m]
[⌈2m⌉,m] ,因此B-树又称作
(
⌈
m
2
⌉
,
m
)
(\lceil\frac{m}{2}\rceil,m)
(⌈2m⌉,m)-树
例如,当 m = 5 m=5 m=5 时,每个结点的分支数上限不能超过 5 5 5,非根结点的一般结点的分支数的下限也不能低于 ⌈ 5 2 ⌉ = 3 \lceil\frac{5}{2}\rceil=3 ⌈25⌉=3,因此 5 5 5 阶B树又称为 ( 3 , 5 ) (3,5) (3,5)-树;当 m = 4 m=4 m=4, 4 4 4 阶B树又称为 ( 2 , 4 ) (2,4) (2,4)-树,而 ( 2 , 4 ) (2,4) (2,4)-树与我们后面要讲到的红黑树又有紧密的关系。
三、B-树的查找
B-树中所存储的记录非常多,因此不便于全部存储在内存中,甚至根本不能由内存容纳。因此我们通常将B-树存放在相对于速度更慢的外存之中。
所谓B-树的查找,其诀窍在于只需要将必须的若干个结点载入内存,通过这种策略可以尽可能的减少I/O的次数。
对于一棵处于活跃状态的B-树而言,我们可以假设其根结点已经载入到内存中。现在假设要查找关键字
k
e
y
key
key,我们先在根结点中顺序查找是否存在该关键字,如果能在某个位置命中,查找结束。假设查找失败于一个特殊的位置,这个位置会存放一个引用,这个引用将会指向B-树中存储在外存中的下一层的某个结点,因此我们通过一次I/O操作找到对应结点,并且将其载入到内存之中,然后我们继续在该结点中进行顺序查找…,依次执行上述操作。
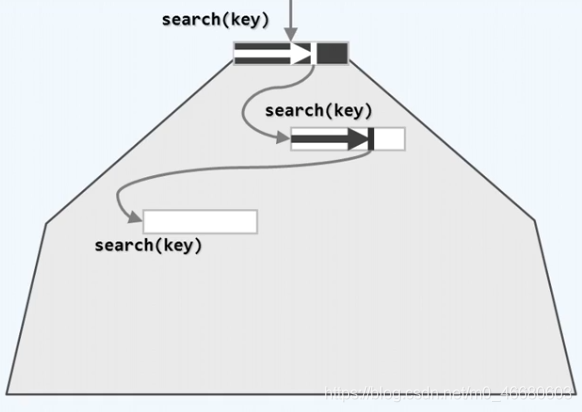
在最坏情况下,这个过程可能反复执行到叶结点,到达叶结点后依然需要进行顺序查找,如果继续失败,则指向叶结点之外的外部引用。
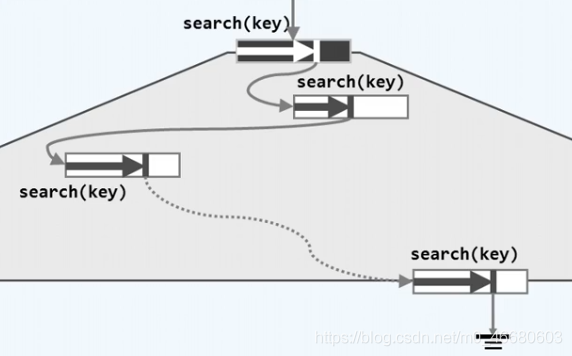
事实上,如果这个外部引用为空,则整个查找以失败告终。但是更多情况下,这个外部引用会指向另一个存储在更低存储层次上的B-树,这样就可以将不同数据规模的B-树串接起来。这也是为什么将这个引用称为“外部结点”。
有的同学可能会提出,能否用二分查找来优化查找结点内部有序关键字呢?事实上,相对于高耗时的I/O操作,这种优化是微乎其微的,甚至可能有害。我们知道一个结点内部的关键字数大概在 200 200 200 ~ 300 300 300,对于这种数量级的关键字,实验表明使用二分查找的效率反而更低。
所谓的B-树的访问,无非就是外存操作(垂直方向)和内存操作(水平方向)交替的过程,有多少次外存操作,就有多少次内存操作。
四、B-树的插入
首先,与B-树的查找的方法一致,在6阶B-树中找到关键字37应该插入的位置,如下图。
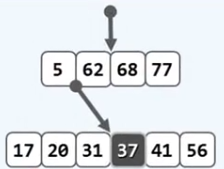
我们知道,
6
6
6 阶B-树的一个结点中最多只可以容纳
5
5
5 个关键字。此时,我们可以发现下层结点中关键字的多于
5
5
5 个,我们称这个结点为上溢结点,需要通过B-树特有的分裂方法调整。
4.1 分裂
- 设上溢结点中的关键字依次为 [ k 0 , . . . , k m − 1 ] [k_0,...,k_{m-1}] [k0,...,km−1]
- 取中位数 s = ⌊ m 2 ⌋ s=\lfloor \frac{m}{2} \rfloor s=⌊2m⌋,以关键字 k s k_s ks 为界划分为 [ k 0 , . . . , k s − 1 ] [k_0,...,k_{s-1}] [k0,...,ks−1], [ k s ] [k_s] [ks], [ k s + 1 , . . . , k m − 1 ] [k_{s+1},...,k_{m-1}] [ks+1,...,km−1] 三个结点
- 关键字 [ k s ] [k_s] [ks] 结点上升一层,并进行分裂操作,将所得的左右另外两个分别作为左、右孩子。
上例中关键字37上升、分裂之后的效果如下图所示。
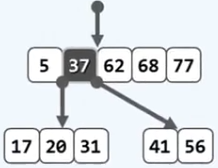
4.2 再分裂
如果上溢结点的父亲结点原本也处于分裂的边缘, [ k s ] [k_s] [ks] 上升之后如果使父亲结点也成为上溢结点,则需要对父结点再次使用分裂操作,成为再分裂。
上溢可能持续发生,并且逐层向上传播;纵然发生了最坏的情况,也不过上溢到根结点。但是,根结点的上溢处理略有不同。如果根结点发生了上溢,则上升的结点 k s k_s ks 将作为整棵B-树的新的根,原先的根节点分裂为2个孩子挂在根结点 [ k s ] [k_s] [ks] 的两侧,如下图。

这也是B-树高度增加的唯一情况。
五、B-树的删除
首先,与B-树的查找的方法一致,在m阶B-树中找到关键字应该删除的位置直接删除即可,但是如果删除之后结点内部的关键字数量过少,即通过删除一个关键字只剩下 ⌈ m 2 ⌉ − 2 \lceil \frac{m}{2} \rceil - 2 ⌈2m⌉−2个结点 ⌈ m 2 ⌉ − 1 \lceil \frac{m}{2} \rceil - 1 ⌈2m⌉−1 个分支。则必须通过旋转和合并操作调整结点。
注意:旋转操作的优先级大于合并操作,只有当旋转操作的条件无法满足时,才进行合并操作。
5.1 旋转
如果发生了下溢,下溢结点首先会左顾右盼看其左右子树是否有盈余(必须是相邻的左右子树,其他兄弟结点不能进行旋转)。这里举例左子树有盈余,则优先朝左子树最后一个结点借。
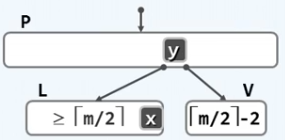
为什么是一定是朝左子树最后一个结点借?因为B-树依然要保证中序遍历的有序性,让
x
x
x 上升到
y
y
y 的位置,再让
y
y
y 下降到下溢结点的第一个位置。这样做则中序遍历依然能够保持有序性。
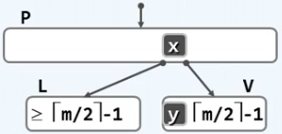
相反的,如果左子树不够借,再看看右子树是否有盈余。如果有,则将右子树第一个结点替换到其父结点的位置,将父结点所对应的元素补充给下溢结点的最后一个位置,这样就能保证中序遍历依然是有序的。
旋转的优先级是高于合并操作的,但是旋转的条件不一定能够满足(左右兄弟不一定有盈余),则需要合并操作。
5.2 合并
发生下溢的结点在经过左顾右盼后,都没有找到可以帮忙的左右结点,旋转操作无法执行。则需要进行合并操作。
此时,左兄弟 和 右兄弟或者不存在,或者所含的关键字均不足 ⌈ m 2 ⌉ \lceil \frac{m}{2} \rceil ⌈2m⌉ 个。
注意:此时还不算糟糕透顶,毕竟左兄弟和右兄弟至少存在一个(因为即使是根结点都有两个子树),且恰巧包含
⌈
m
2
⌉
−
1
\lceil \frac{m}{2} \rceil - 1
⌈2m⌉−1 个关键字,这里不妨以存在左兄弟为例。
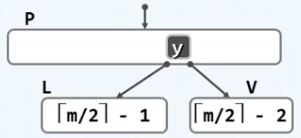
此时,无论是结点
L
L
L 还是下溢结点
V
V
V,关键字的个数都非常的少,并且
[
L
]
[L]
[L]、
[
y
]
[y]
[y]、
[
V
]
[V]
[V] 三个结点的总和关键字的个数都不会超过结点的关键字上界
m
−
1
m - 1
m−1,因此直接将其三者合并(原先
[
y
]
[y]
[y] 左右两个分支也合并为一个指针指向合并结点),来解决结点
V
V
V 的下溢问题。
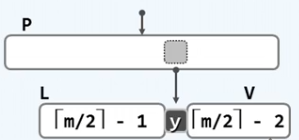
通过合并之后,依然能够保持中序遍历的有序性。
但是问题还没有结束,通过合并以后,上层的父结点失去了一个关键字,父结点有可能因此发生了下溢。因此再尝试对父结点进行旋转,如果无法旋转,则继续合并,如法炮制。跟旋转操作一样,最坏情况下,也只是达到了树根。
补充:B+树
因为B+树不是本章的重点,但是既然讲到了B-树,那么也理应带上一点B+树的影子。在这里我就直接引用另外一个作者的文章,供大家参考:【B+树和B树的区别】






















 859
859











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










