《我的第一本算法书》笔记-第1章 数据结构

第 1 章 数据结构

1-1 什么是数据结构

数据存储于内存时，决定了数据顺序和位置关系的便是“数据结构”。所谓结构就是关系，是数据元素本身的特性及数据元素直接的关系。将数据存储于内存时，根据使用目的选择合适的数据结构，可以提高内存的利用率。

数据在内存中是呈线性排列的，但是我们也可以使用指针等道具，构造出类似“树形”的复杂结构。

1-2 链表

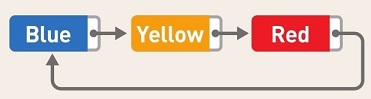
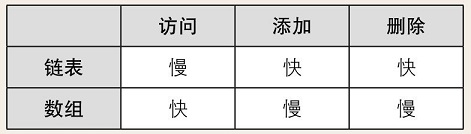
链表是数据结构之一，其中的数据呈线性排列。在链表中，数据的添加和删除都比较方便，就是访问比较耗费时间。

上图为链表的概念图，每个数据都有1个“指针”，它指向下一个数据的内存地址。

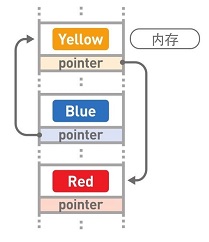
在链表中，数据一般都是分散存储于内存中的，无需存储在连续空间内。

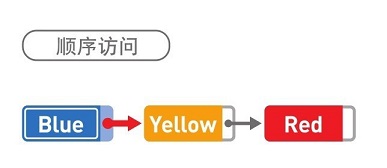
因为数据都是分散存储的，所以如果想要访问数据，只能从第1个数据开始，顺着指针的指向一一往下访问（这便是顺序访问）。

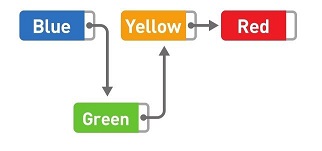
如果想要添加数据，只需要改变添加位置前后的指针指向就可以。比如，在Blue和Yellow之间添加Green，将Green的指针指向Yellow，然后再把Blue的指针指向的位置变成Green（需要注意原书此处的描述是错误的）。

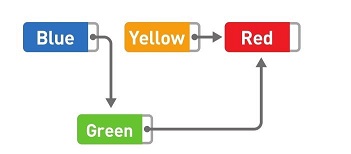
数据的删除也是一样，只要改变指针的指向就可以。比如删除Yellow，这时只需要把Green指针指向的位置从Yellow变成Red，删除就完成了。

我们把链表中的数据量记成n，访问数据时，我们需要从链表头部开始查找（线性查找），如果目标数据在链表最后的话，需要的时间就是O(n)。添加数据只需要更改两个指针的指向，所以耗费的时间与n无关。如果已经到达了添加数据的位置，那么添加操作只需要花费O(1)的时间，删除同理。

循环链表或环形链表：在链表尾部使用指针，并且让它指向链表头部的数据，将链表变成环形。此种链表没有头和尾的概念。

双向链表：每个数据设定为两个指针，分别指向前后数据。使用这种链表，不仅可以从前往后，还可以从后往前遍历数据，十分方便。缺点：1、指针数的增加会导致存储空间需求增加；2、添加和删除数据时需要改变更多指针的指向。

1-3 数组

数组也是数据呈线性排列的一种数据结构。与链表不同，在数组中，访问数据十分简单，而添加和删除数据比较耗工夫。

这就是数组的概念图。Blue、Yellow、Red作为数据存储在数组中。

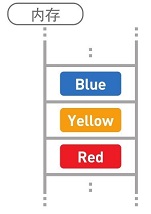
数据按顺序存储在内存的连续空间内。

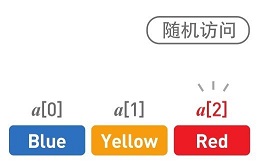
由于数据是存储在连续空间内的，所以每个数据的内存地址（在内存上的位置）都可以通过数组下标算出，我们也就可以借此直接访问目标数据（这叫作“随机访问”）。比如现在我们想要访问Red。如果使用指针就只能从头开始查找，但在数组中，只需要指定a[2]，便能直接访问Red。

如果想在任意位置上添加或者删除数据，数组的操作就要比链表复杂多了。这里我们尝试将Green添加到第2个位置上。首先，在数组的末尾确保需要增加的存储空间。为了给新数据腾出位置，要把已有数据一个个移开。首先把Red往后移。然后把Yellow往后移。最后在空出来的位置上写入Green。




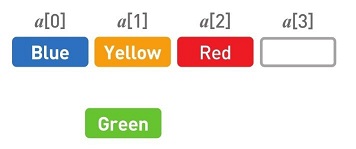
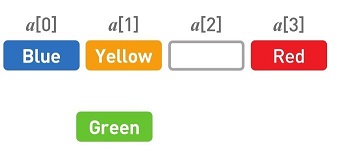
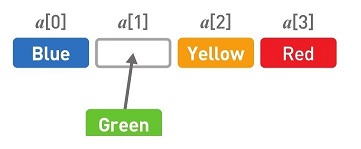
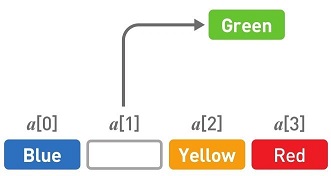
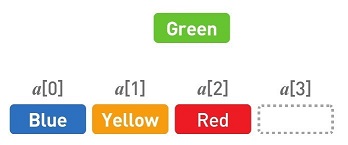
如果想要删除Green，首先，删掉目标数据（在这里指Green）。然后把后面的数据一个个往空位移。先把Yellow往前移。接下来移动Red。最后再删掉多余的空间。这样一来Green便被删掉了。


假设数组中有n个数据，由于访问数据时使用的是随机访问（通过下标可计算出内存地址），所以需要的运行时间仅为恒定的O(1)。但另一方面，想要向数组中添加新数据时，必须把目标位置后面的数据一个个移开。所以，如果在数组头部添加数据，就需要O(n)的时间。删除操作同理。

1-4 栈

栈也是一种数据呈线性排列的数据结构，不过在这种结构中，我们只能访问最新添加的数据。栈就像是一摞书，拿到新书时我们会把它放在书堆的最上面，取书时也只能从最上面的新书开始取（可以看做是向空箱子里面放东西，先放进去的在下面，后放进去的再上边，取的时候先取上面的）。


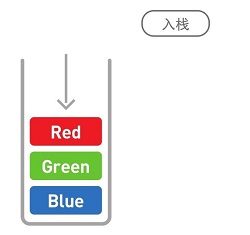
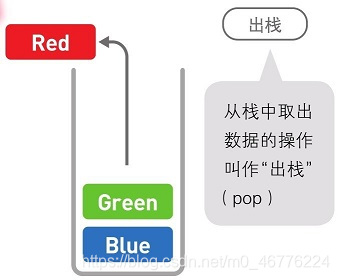
像栈这种最后添加的数据最先被取出，即“后进先出”的结构，我们称为Last InFirst Out，简称LIFO。与链表和数组一样，栈的数据也是线性排列，但在栈中，添加和删除数据的操作只能在一端进行，访问数据也只能访问到顶端的数据。想要访问中间的数据时，就必须通过出栈操作将目标数据移到栈顶才行。只能在一端操作这一点看起来似乎十分不便，但在只需要访问最新数据时，使用它就比较方便。

1-5 队列

队列中的数据也呈线性排列。就和“队列”这个名字一样，把它想象成排成一队的人更容易理解。在队列中，处理总是从第一名开始往后进行，而新来的人只能排在队尾。


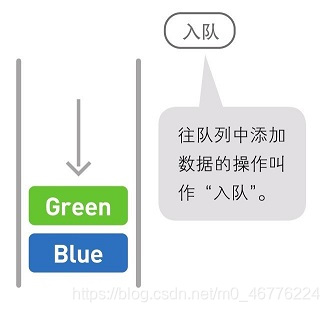
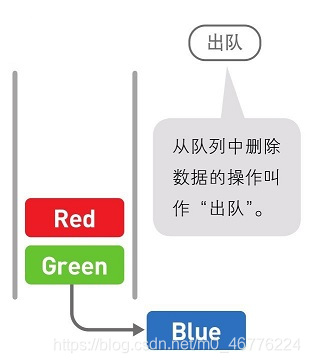
像队列这种最先进去的数据最先被取来，即“先进先出”的结构，我们称为FirstIn First Out，简称FIFO。与栈类似，队列中可以操作数据的位置也有一定的限制。在栈中，数据的添加和删除都在同一端进行，而在队列中则分别是在两端进行的。队列也不能直接访问位于中间的数据，必须通过出队操作将目标数据变成首位后才能访问。

1-6 哈希表

在哈希表这种数据结构中，可以使数据的查询效率得到显著提升。

哈希表存储的是由键（key）和值（value）组成的数据。例如，我们将每个人的性别作为数据进行存储，键为人名，值为对应的性别。

首先准备好数组，我们用5个箱子的数组来存储数据。尝试把Joe存进去。使用哈希函数（Hash）计算Joe的键，也就是字符串“Joe”的哈希值。得到的结果为4928（哈希函数的详细说明在5-3节）。

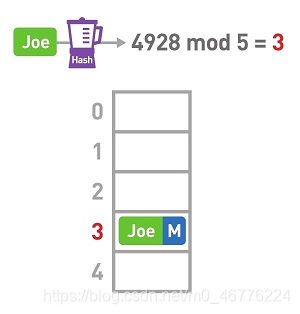
将得到的哈希值除以数组的长度5，求得其余数。这样的求余运算叫作“mod运算”。此处mod运算的结果为3。因此，我们将Joe的数据存进数组的3号箱子中。重复前面的操作，将其他数据也存进数组中。

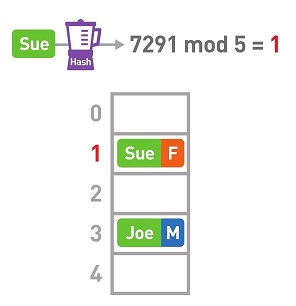
Nell键的哈希值为6276, mod 5的结果为1。本应将其存进数组的1号箱中，但此时1号箱中已经存储了Sue的数据。这种存储位置重复了的情况便叫作“冲突”。遇到这种情况，可使用链表在已有数据的后面继续存储新的数据。


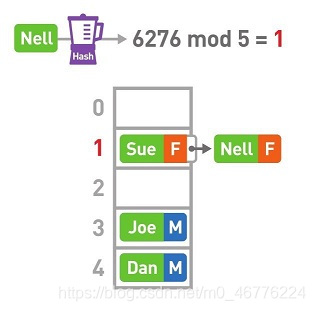
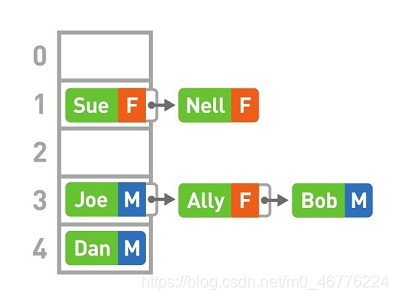
像这样存储完所有数据，哈希表也就制作完成了。

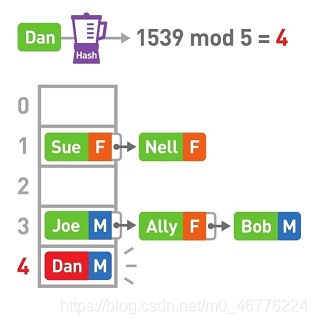
假设我们要查询Dan的性别。首先需要算出Dan键的哈希值，然后对其进行mod运算。最后得到的结果为4，于是我们知道了它存储在4号箱中。

想要查询Ally的性别时先要算出Ally键的哈希值，再对其进行mod运算。最终得到的结果为3。

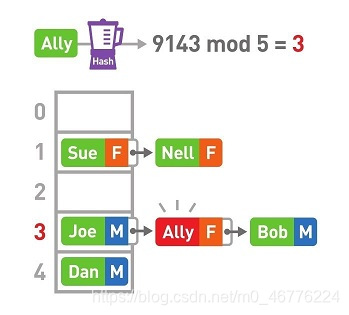
然而3号箱中数据的键是Joe而不是Ally。此时便需要对Joe所在的链表进行线性查找。

在哈希表中，我们可以利用哈希函数快速访问到数组中的目标数据。如果发生哈希冲突，就使用链表进行存储。这样一来，不管数据量为多少，我们都能够灵活应对。这种方法被称为“链地址法”。除此之外，还有几种解决冲突的方法。其中，应用较为广泛的是“开放地址法”。这种方法是指当冲突发生时，立刻计算出一个候补地址（数组上的位置）并将数据存进去。如果仍然有冲突，便继续计算下一个候补地址，直到有空地址为止。可以通过多次使用哈希函数或“线性探测法”等方法计算候补地址。

如果数组的空间太小，使用哈希表的时候就容易发生冲突，线性查找的使用频率也会更高；反过来，如果数组的空间太大，就会出现很多空箱子，造成内存的浪费。因此，给数组设定合适的空间非常重要。

1-7 堆

堆是一种图的树形结构，被用于实现“优先队列”（priority queues）（树形结构的详细讲解在4-2节）。优先队列是一种数据结构，可以自由添加数据，但取出数据时要从最小值开始按顺序取出。在堆的树形结构中，各个顶点被称为“结点”（node），数据就存储在这些结点中。

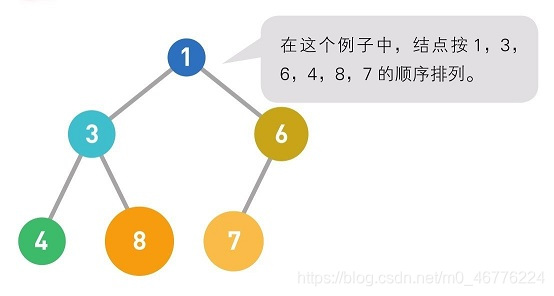
结点内的数字就是存储的数据。堆中的每个结点最多有两个子结点。树的形状取决于数据的个数。另外，结点的排列顺序为从上到下，同一行里则为从左到右。

在堆中存储数据时必须遵守这样一条规则：子结点必定大于父结点。因此，最小值被存储在顶端的根结点中。往堆中添加数据时，为了遵守这条规则，一般会把新数据放在最下面一行靠左的位置。当最下面一行里没有多余空间时，就再往下另起一行，把数据加在这一行的最左端。

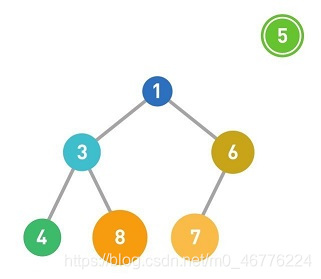
往堆里添加数字5。

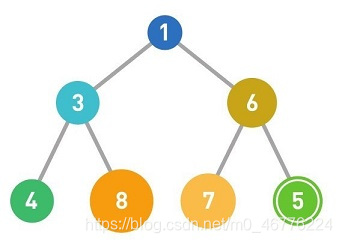
图中最下面一排空着一个位置，所以将数据加在此处。

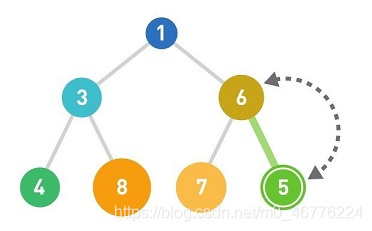
如果父结点大于子结点，则需要交换父子结点的位置。重复这样的操作直到数据都符合规则，不再需要交换为止。

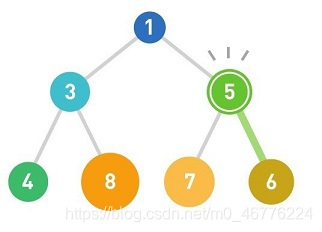
至此添加完成。

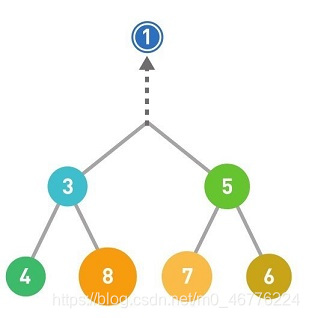
从堆中取出数据时，取出的是最上面的数据。这样，堆中就能始终保持最上面的数据最小。由于最上面的数据被取出，因此堆的结构也需要重新调整。

将最后的数据（此处为6）移动到最顶端。

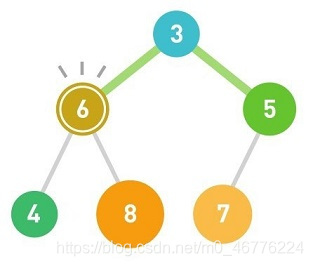
如果子结点的数字小于父结点的，就将父结点与其左右两个子结点中较小的一个进行交换。重复这个操作直到数据都符合规则，不再需要交换为止。

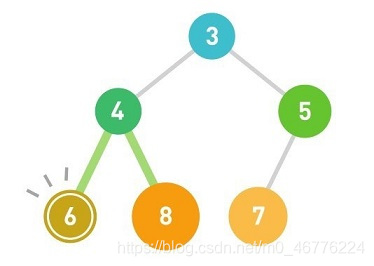
这样，从堆中取出数据的操作便完成了。

堆中最顶端的数据始终最小，所以无论数据量有多少，取出最小值的时间复杂度都为O(1)。另外，因为取出数据后需要将最后的数据移到最顶端，然后一边比较它与子结点数据的大小，一边往下移动，所以取出数据需要的运行时间和树的高度成正比。假设数据量为n，根据堆的形状特点可知树的高度为log₂n，那么重构树的时间复杂度便为O(logn)。添加数据也一样。在堆的最后添加数据后，数据会一边比较它与父结点数据的大小，一边往上移动，直到满足堆的条件为止，所以添加数据需要的运行时间与树的高度成正比，也是O(logn)。

1-8 二叉查找树

二叉查找树（又叫作二叉搜索树或二叉排序树）是一种数据结构，采用了图的树形结构。数据存储于二叉查找树的各个结点中。此处以不存在相同数字为前提进行说明。

二叉查找树有两个性质：

1. 每个结点的值均大于其左子树上任意一个结点的值；
2. 每个结点的值均小于其右子树上任意一个结点的值。

根据这两个性质可以得到以下结论：

1. 二叉查找树的最小结点要从顶端开始，往其左下的末端寻找；
2. 二叉查找树的最大结点要从顶端开始，往其右下的末端寻找。
   
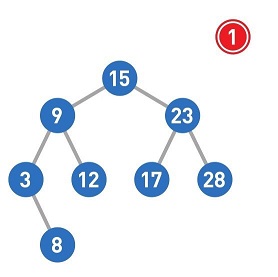
   下面我们来试着往二叉查找树中添加数据。比如添加数字1。
   
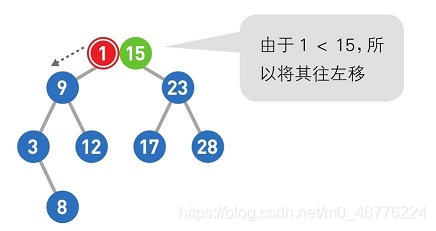
   首先，从二叉查找树的顶端结点开始寻找添加数字的位置。将想要添加的1与该结点中的值进行比较，小于它则往左移，大于它则往右移。
   
   
   
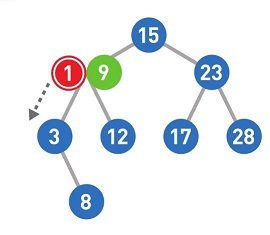
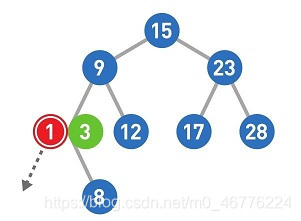
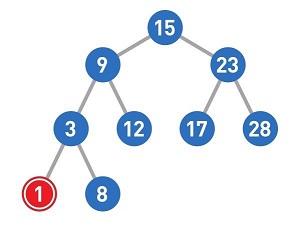
   这样，1的添加操作便完成了。
   
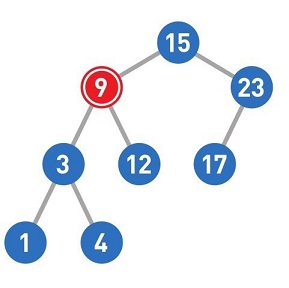
   接下来我们来试试删除结点9。

如果需要删除的结点有两个子结点，那么先删掉目标结点，然后在被删除结点的左子树中寻找最大结点，最后将最大结点移到被删除结点的位置上。这样一来，就能在满足二叉查找树性质的前提下删除结点了。如果需要移动的结点（此处为4）还有子结点，就递归执行前面的操作。



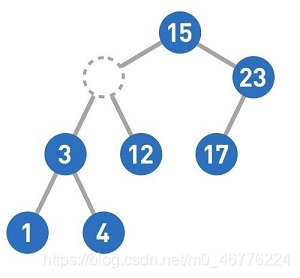
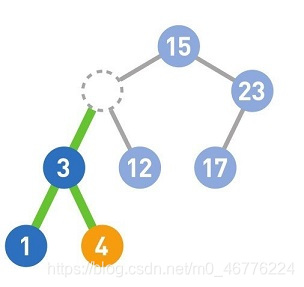
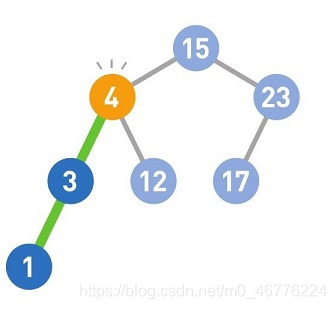
这样，9的删除操作便完成了。

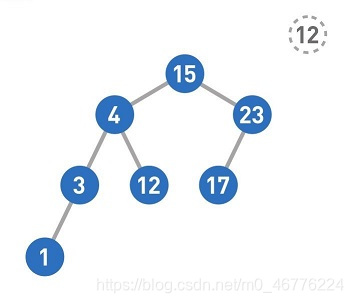
下面我们来试试查找12。

从二叉查找树的顶端结点开始往下查找。和添加数据时一样，把12和结点中的值进行比较，小于该结点的值则往左移，大于则往右移。


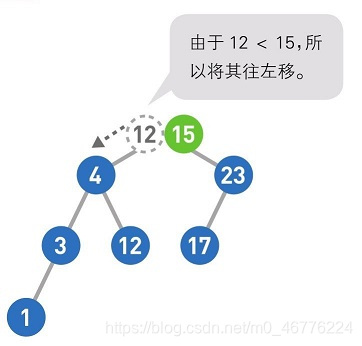
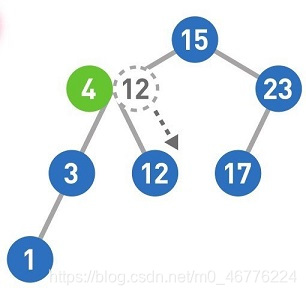
这样，我们就完成了查找操作。

我们可以把二叉查找树当作是二分查找算法思想的树形结构体现。因为它具有前面提到的那两个性质，所以在查找数据或寻找适合添加数据的位置时，只要将其和现有的数据比较大小，就可以根据比较结果得知该往哪边移动了。比较的次数取决于树的高度。所以如果结点数为n，而且树的形状又较为均衡的话，比较大小和移动的次数最多就是log₂n。因此，时间复杂度为O(logn)。但是，如果树的形状朝单侧纵向延伸，树就会变得很高，此时时间复杂度也就变成了O(n)。