Java方法（下）-CSDN博客

本文链接：https://blog.csdn.net/m0_48677434/article/details/137726757

1.1 方法的可变参数（一般重要）

规则要求

【修饰符】 class 类名{
    【①修饰符】 ②返回值类型  ③方法名(④数据类型... 参数名){
        ⑤方法体语句;
    }
    
    【①修饰符】 ②返回值类型  ③方法名(④数据类型 参数名1, 数据类型 参数名2, 数据类型... 参数名3){
        ⑤方法体语句;
    }
 }

方法的形参列表中出现 “数据类型 ... 参数名”这个部分，就是可变参数。

可变：实参的个数可变

可变参数有要求：

一个方法的形参列表中，最多只能有1个可变参数
可变参数必须是最后一个

区别：数组类型的形参与可变参数的形参，即(元素类型[] 数组名) 与 (元素类型... 可变参数名)

从接收实参的角度来说，可变参数更灵活
- (元素类型[] 数组名) ：实参必须传入对应类型的数组
- (元素类型... 可变参数名) ：实参可以传入 0 ~ n 个的元素，也可以接收1个对应类型的数组
从适用性来说，数组类型更灵活
- 因为可变参数一个方法只能有1个，而且必须是最后一个
- 但是数组类型的形参，没有这个要求

案例1

public class TestVarParam {
    //声明一个新的方法，用来求【任意个】整数的和
    public static int add(int[] arr){
        int sum = 0;
        for (int i = 0; i < arr.length; i++) {
            sum += arr[i];
        }
        return sum;
    }

    //声明一个新的方法，用来求【任意个】整数的和
    public static int total(int... arr){//在声明可变参数的方法里面，把可变参数当成数组使用即可
        int sum = 0;
        for (int i = 0; i < arr.length; i++) {
            sum += arr[i];
        }
        return sum;
    }


    public static void main(String[] args) {
        //调用add方法
        //求1,2,3,4,5的和
        System.out.println(add(new int[]{1,2,3,4,5}));//直接输出结果
        //求：1,8,9,7的和
        System.out.println(add(new int[]{1,8,9,7}));//直接输出结果
        //求：5的和
        System.out.println(add(new int[]{5}));//直接输出结果
        //求：0个元素的和
//        System.out.println(add());//错误，因为形参类型是int[]，就必须给它数组
        System.out.println(add(new int[0]));
        System.out.println(add(new int[]{}));

        System.out.println("======================");
        //调用total方法
        //求1,2,3,4,5的和
        System.out.println(total(1,2,3,4,5));
        //求：1,8,9,7的和
        System.out.println(total(1,8,9,7));
        //求：5的和
        System.out.println(total(5));
        //求：0个元素的和
        System.out.println(total());

        //求1,2,3,4,5的和
        System.out.println(total(new int[]{1,2,3,4,5}));//直接输出结果
        //求：1,8,9,7的和
        System.out.println(total(new int[]{1,8,9,7}));//直接输出结果
        //求：5的和
        System.out.println(total(new int[]{5}));//直接输出结果
        //求：0个元素的和
        System.out.println(total(new int[]{}));//直接输出结果
    }
}

案例2

public class TestVarParam2 {
    //定义一个新方法，可以实现 将任意个字符串进行拼接，每两个字符串之间使用某个字符进行连接
    //separator：分隔符
    public static String concat(char separator, String... args){
        String str = "";//空字符串
        for (int i = 0; i < args.length; i++) {
            str += (i==0 ? "" :separator) + args[i];
        }
        /*
        i=0   str += "" + args[0];   str += "" + "hello";           str ="hello"
        i=1   str += separator + args[1];   str += '-' + "world";   str = "hello-world"
         */
        return str;
    }


    public static void main(String[] args) {
        //用-连接  hello  world  java 这些字符串
        System.out.println(concat('-', "hello", "world", "java"));
        //hello-world-java

        //用-连接  0个字符串
//        System.out.println(concat());
        //错误的，因为(char separator, String... args)中 char separator部分不是可变参数，那么就得和原来一样，传入对应个数、类型的实参
        System.out.println(concat(' '));
    }
}

练习题

（1）声明如下方法：

声明方法int min(int... nums)：返回n个整数中的最小值
声明方法int maxApproximate(int... nums)：返回n个整数的最大公约数

（2）在测试类的main方法中调用测试

/*
（1）声明如下方法：
- 声明方法int min(int... nums)：返回n个整数中的最小值
- 声明方法int maxApproximate(int... nums)：返回n个整数的最大公约数
（2）在测试类的main方法中调用测试
 */
public class VarParamExercise5 {
    public static void main(String[] args) {
        //测试找最小值的方法min
        System.out.println("4,6,2,3最小值：" + min(4,6,2,3));
        System.out.println("6,12,9小值：" + min(6,12,9));

        //测试maxApproximate方法
        System.out.println("4,6,2,3公约数：" + maxApproximate(4,6,2,3));
        System.out.println("6,12,9公约数：" + maxApproximate(6,12,9));

//        System.out.println(Integer.MAX_VALUE);//2147483647

//        System.out.println("找0个整数的最小值：" +min());
    }

    /*
    例如：6,12,9       公约数：1,3
        思路：
        （1）先找到它们中最小的值  6
        （2）从6开始往回找[6->1]，找到的第一个公约数，就是最大公约数   第1个找到的是3,3就是它们的最大公约数
     */
    public static int maxApproximate(int... nums){
        //(1)找到nums这组数中的最小值
        int min = min(nums);
        //(2)在 [min -> 1]范围内找 nums这组数公约数
        for(int i=min; i>=1; i--){
            //判断i是不是nums[0],nums[1],,,nums[最后的下标]它们共同的公约数
            boolean flag = true;//假设i是它们的公约数
            for(int j=0; j<nums.length; j++){
                //if(nums[j] % i == 0)//一次条件成立，只能说明i是nums[j]这一个数的公约数
//                if(nums[j] % i != 0)//一次条件成立，说明 i一定不是他们的公约数，因为i已经不是nums[j]的约数
                if(nums[j] % i != 0){//内循环如果一次都没有满足这个if，说明i把每一个nums[j]整除，说明i是它们的公约数
                                    //如果没有进入这个if，flag是true
                    flag = false;
                    break;
                }
            }
            if(flag){
                return i;
            }
        }
        return 1;//当上面的循环没进入，默认返回1
    }

    //声明方法int min(int... nums)：返回n个整数中的最小值
    public static int min(int... nums){
        //方法名min 与 变量名min可以重名
        int min = nums[0];
        for (int i = 1; i < nums.length; i++) {
            if(nums[i] < min){
                min = nums[i];
            }
        }
        return min;
    }//上面这么写也对.当min()没有传入实参的时候，会发生ArrayIndexOutOfBoundsException

    /*public static int min(int... nums){
        //方法名min 与 变量名min可以重名
        int min = Integer.MAX_VALUE;//把变量min初始化为一个很大的数，这个数是int的最大值 2147483647
        for (int i = 0; i < nums.length; i++) {
            if(nums[i] < min){
                min = nums[i];
            }
        }
        *//*
        假设这组数是 6,12,5
            i=0   if(num[0]<min)成立  if(6<2147483647)成立  min = 6
            i=1   if(num[1] < min)   if(12 < 6)不成立
            i=2   if(num[2] < min)   if(5 < 6)成立   min=5
         *//*
        return min;
    }*///下面的写法，当min()没有传入实参的时候，不会发生ArrayIndexOutOfBoundsException
}

1.2 方法的重载（非常重要）

1.2.1 什么是方法的重载？

方法的重载（Overload），是指在同一个类中（或者父子类中（后面会将））出现两个或多个==方法的名称相同==，==形参列表不同==，这样的两个或多个方法称为重载。

序号	方法的构成	重载的方法
0	位置	在同一个类中（现在），或父子类中
1	修饰符	不看
2	返回值类型	不看
3	方法名	必须相同
4	(形参列表)	必须不同，可以个数、类型、顺序不同。一般都是个数或类型不同。
5	{方法体}	不看

如果方法有重载，调用重载的方法时，匹配的原则：

先找类型、个数、顺序最最匹配
如果没有最最匹配，找可以兼容的，但是不能有同时多个都兼容，兼容程度相同。
- 例如：可以通过类型的自动升级匹配
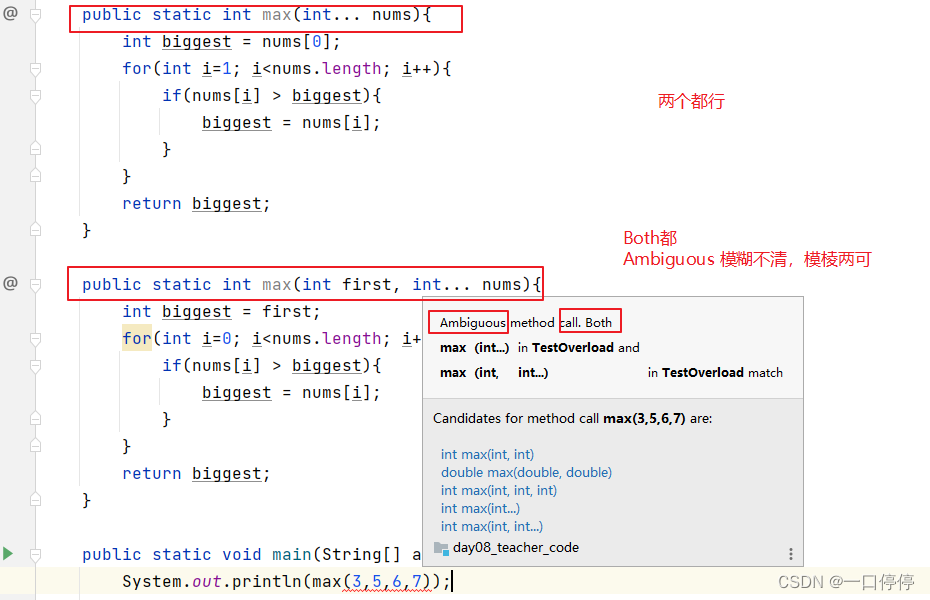
如果找不到匹配的，也找不到兼容，或者找到多个同时兼容的（兼容程度一样），都会报错。

1.2.2 方法重载的演示

需求：

定义一个方法，可以求2个整数的最大值
定义一个方法，可以求2个小数的最大值
定义一个方法，可以求3个整数的最大值

public class TestOverload {
//    - 定义一个方法，可以求2个整数的最大值
    public static int max(int a, int b){
        return a > b ? a : b;
    }

    //- 定义一个方法，可以求2个小数的最大值
    public static double max(double a, double b){
        return a > b ? a : b;
    }

    //- 定义一个方法，可以求3个整数的最大值
    public static int max(int a, int b, int c){
        int bigger =  a > b ? a : b;
        return bigger > c ? bigger : c;
    }

    public static int max(int... nums){
        int biggest = nums[0];
        for(int i=1; i<nums.length; i++){
            if(nums[i] > biggest){
                biggest = nums[i];
            }
        }
        return biggest;
    }

    /*public static int max(int first, int... nums){//没必要写它
        int biggest = first;
        for(int i=0; i<nums.length; i++){
            if(nums[i] > biggest){
                biggest = nums[i];
            }
        }
        return biggest;
    }*/

    public static void main(String[] args) {
        //调用max方法
        System.out.println(max(5,6));//匹配 int max(int a, int b)
        System.out.println(max(5.0,6.0));//匹配 double max(double a, double b)
        System.out.println(max(5,4,7));//匹配  int max(int a, int b, int c)

//        System.out.println(max(5.0,6.0,7.0));//报错，因为没有可以匹配的
        System.out.println(max(5.0,6));//没有报错，匹配  double max(double a, double b)  6被自动升级为6.0
//        System.out.println(max(3,5,6,7));//报错，有两个方法同时都兼容，兼容程度一样
    }
}

1.2.3 练习题

练习题7

（1）声明如下方法：

int compare(int a, int b)：比较两个整数大小关系，如果第一个整数比第二个整数大，则返回正整数，如果第一个整数比第二个整数小，则返回负整数，如果两个整数相等则返回0；
int compare(double a, double b)：比较两个小数大小关系，如果第一个小数比第二个小数大，则返回正整数，如果第一个小数比第二个小数小，则返回负整数，如果两个小数相等则返回0；
int compare(char a, char b)：比较两个字符大小关系，如果第一个字符比第二个字符编码值大，则返回正整数，如果第一个字符比第二个字符编码值小，则返回负整数，如果两个字符相等则返回0；

（2）在测试类的main方法中调用，分别比较

public class OverloadExercise7 {
    public static void main(String[] args) {
        System.out.println(compare(4, 7));//-3  代表4<7的意思
        System.out.println(compare(15.6, 9.6));//1 代表15.6>9.6
        System.out.println(compare('尚','硅'));//-7211 代表'尚' < '硅'
        System.out.println(compare('谷','硅'));//5106 代表'谷' > '硅'
    }

    /*
    定义一个方法，可以比较两个整数的大小关系。
    两个整数的大小关系有几种情况？
    3种情况：
    （1）a > b
    （2）a < b
    （3）a = b
    返回1个结果，让使用这个方法的人，一看结果就知道是3种情况的哪一种。
    无论a,b是什么类型，Java里面有一个约定：
        返回的是正整数结果，那么就代表 a>b， 正整数的值是多少也不重要，可以是1，可以是100，可以是89
        返回的是负整数结果，那么就代表 a<b，
        返回的是0结果，那么就代表 a=b，
     */
    public static int compare(int a,int b){
        /*
        if(a > b){
            return 1;//正数就行，什么值都可以
        }else if(a < b){
            return -1; //负数就行，什么值都可以
        }else{
            return 0;
        }
        //上面代码是对的， if-else if-else，如果前两个条件不满足，默认执行else
         */

     /*   if(a > b){
            return 1;//正数就行，什么值都可以
        }else if(a < b){
            return -1; //负数就行，什么值都可以
        }else if(a==b){
            return 0;
        }//错误的，编译器会认为，if-else if - else if结构，就存在3个if都不进去，那么就可能没有结果返回*/

        return a - b;
    }

    public static int compare(double a, double b){
//        return a - b;//错误，a-b的结果是double，不符合int类型结果要求
    //    return (int)(a-b);//语法上看起来可以，但是有点小问题
            //当 a = 2.5 ,b = 2.3   (int)(a-b)结果是(int)0.2结果是0  代表相等
        if(a > b){
            return 1;//正数就行，什么值都可以
        }else if(a < b){
            return -1; //负数就行，什么值都可以
        }else{
            return 0;
        }
    }

    public static int compare(char a, char b){
        return a - b;//用两个char字符的编码值计算
    }


}

练习题8

（1）声明一个数组工具类包含几个重载方法

重载方法系列1：可以为int[]，double[]，char[]数组实现从小到大排序
- void sort(int[] arr)
- void sort(double[] arr)
- void sort(char[] arr)
重载方法系列2：toString方法，可以遍历int[]，double[]，char[]数组，遍历结果形式：[元素1，元素2，。。。]
- String toString(int[] arr)
- String toString(double[] arr)
- String toString(char[] arr)

（2）在测试类的main方法中调用

/*
ctrl + Shift +  -：收拢所有方法
ctrl + Shift +  +：展开所有方法
Ctrl + alt + M：选中一段代码，按这个快捷键，就会把这段代码抽出来放到一个新方法中，新方法由我们自己取名字
 */

public class OverloadExercise8 {
    //定义一个方法，用冒泡排序，实现给一个int[]数组排序，从小到大
    public static void sort(int[] arr){
        //外循环，控制几轮， arr.length个元素，比较 arr.length-1轮
        //i的范围[1, arr.length-1]
        for(int i=1; i<=arr.length-1; i++){
            //内循环，控制每一轮比较几次，哪些元素在比较
            /*
            假设 arr.length=4
            i=1,第一轮
                arr[0]~arr[1]
                arr[1]~arr[2]
                arr[2]~arr[3]
                arr[j]~arr[j+1]
                for(int j=0; j<3; j++)  for(int j=0; j<arr.length-i; j++)
            i=2,第2轮
                arr[0]~arr[1]
                arr[1]~arr[2]
                //arr[2]~arr[3] 可以不比较
                arr[j]~arr[j+1]
                for(int j=0; j<2; j++) for(int j=0; j<arr.length-i; j++)
             i=3,第3轮
                arr[0]~arr[1]
                //arr[1]~arr[2] 可以不比较
                //arr[2]~arr[3] 可以不比较
                arr[j]~arr[j+1]
                for(int j=0; j<1; j++) for(int j=0; j<arr.length-i; j++)

             */
            for(int j=0; j<arr.length-i; j++){
                if(arr[j] > arr[j+1]){
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
            }
        }
    }
    public static void printIntArray(int[] nums) {
        for (int i = 0; i < nums.length; i++) {
            System.out.print(nums[i]+" ");
        }
        System.out.println();
        //遍历int[]数组的元素，直接输出到控制台
    }

    public static String toString(int[] arr){
        //遍历int[]数组的元素，先拼接为一个String，返回给调用者，由它决定是输出还是干什么
        //拼接之后的结果：[5,6,7,4,1]
        String str = "";
        for (int i = 0; i < arr.length; i++) {
            str += (i==0 ?"[":",") + arr[i];
        }

        return str +"]";
    }

    public static void sort(double[] arr){
        //外循环，控制几轮， arr.length个元素，比较 arr.length-1轮
        //i的范围[1, arr.length-1]
        for(int i=1; i<=arr.length-1; i++){
            //内循环，控制每一轮比较几次，哪些元素在比较
            for(int j=0; j<arr.length-i; j++){
                if(arr[j] > arr[j+1]){
                    double temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
            }
        }
    }
    public static String toString(double[] arr){
        String str = "";
        for (int i = 0; i < arr.length; i++) {
            str += (i==0 ?"[":",") + arr[i];
        }

        return str +"]";
    }
    public static void sort(char[] arr){
        //外循环，控制几轮， arr.length个元素，比较 arr.length-1轮
        //i的范围[1, arr.length-1]
        for(int i=1; i<=arr.length-1; i++){
            //内循环，控制每一轮比较几次，哪些元素在比较
            for(int j=0; j<arr.length-i; j++){
                if(arr[j] > arr[j+1]){
                    char temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
            }
        }
    }
    public static String toString(char[] arr){
        String str = "";
        for (int i = 0; i < arr.length; i++) {
            str += (i==0 ?"[":",") + arr[i];
        }

        return str +"]";
    }

    public static void main(String[] args) {
        int[] nums = {5,6,7,4,1};
        sort(nums);
//        printIntArray(nums);
        String str = toString(nums);
        System.out.println(str);
        System.out.println("====================");
        double[] price = {89.5, 99.9, 9.9};
        sort(price);
        System.out.println(toString(price));

        System.out.println("====================");
        char[] letters = {'b','h','a','k','m'};
        sort(letters);
        System.out.println(toString(letters));
    }
}

练习题9

（1）声明两个重载方法

方法1：double triangleArea(double base, double height),根据底边和高，求三角形面积，
方法2：double triangleArea(double a, double b, double c),根据三条边，求三角形面积，根据三角形三边求面积的海伦公式：

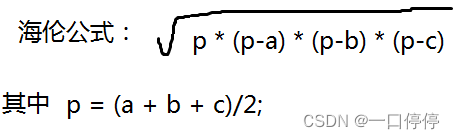
提示：Math.sqrt(x)，求x的平方根

（2）在测试类的main方法中调用

public class OverloadExercise9 {
    /**
     * 求三角形的面积
     *
     * @param base   double 三角形的底边
     * @param height double 三角形该底边对应的高
     * @return double 三角形的面积
     */
    public static double triangleArea(double base, double height) {
        return (base * height) / 2;
    }

    /**
     * 也是求三角形面积
     *
     * @param a double 第一个边长的值
     * @param b double 第二个边长的值
     * @param c double 第三个边长的值
     * @return double 三角形的面积
     */
    public static double triangleArea(double a, double b, double c) {
        if(a<=0 || b<=0 || c<=0 || a+b<=c || b+c<=a ||a+c<=b){//无法构成三角形的情况
            System.out.println(a +"," + b +"," +c +"的值无法构成三角形");
            return 0.0;
        }
        double p = (a + b + c) / 2;
       return Math.sqrt( p * (p-a) * (p-b) * (p-c));
    }

    /**
     * 主方法，Java程序的入口
     * @param args String[] 主方法的形参列表，它可以通过程序参数方式传入实参
     */
    public static void main(String[] args) {
        double base = 4;
        double height = 3;
        System.out.println("底边是4，高是3的三角形面积：" + triangleArea(base, height));

        double a = 3;
        double b = 4;
        double c = 5;
        System.out.println("底边分别为3,4,5的三角形面积：" + triangleArea(a,b,c));

        double x = 3;
        double y = 5;
        double z = 1;
        //违反三角形边长的要求：任意两边之和大于第三边，否则无法构成三角形
        System.out.println("底边分别为3,5,1的三角形面积：" + triangleArea(x,y,z));//NaN
    }
}

1.3 文档注释（了解）

/**
注释内容
*/
【修饰符】 class 类名{
    /**
    对方法的功能进行解释。
    @param 形参名1 形参的类型 对第1个形参进行解释说明
    @param 形参名2 形参的类型 对第2个形参进行解释说明
    @return 返回值类型 对返回值进行解释说明
    */
     【①修饰符】 ②返回值类型  ③方法名(【④形参列表】){
        ⑤方法体语句;
    }
    //如果方法没有形参，就不用写@param，如果方法的返回值类型是void，就不用写@return
}

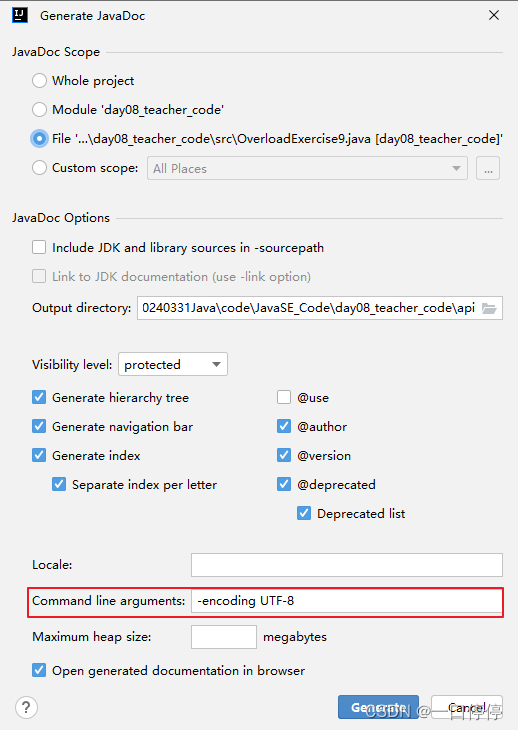
文档注释可以配合javadoc.exe工具生成API文档。

/**
 * 这是一个演示文档注释的类
 * @version 1.0
 * @author cjq
 */

public class OverloadExercise9 {
    /**
     * 求三角形的面积
     *
     * @param base   double 三角形的底边
     * @param height double 三角形该底边对应的高
     * @return double 三角形的面积
     */
    public static double triangleArea(double base, double height) {
        return (base * height) / 2;
    }

    /**
     * 也是求三角形面积
     *
     * @param a double 第一个边长的值
     * @param b double 第二个边长的值
     * @param c double 第三个边长的值
     * @return double 三角形的面积
     */
    public static double triangleArea(double a, double b, double c) {
        if(a<=0 || b<=0 || c<=0 || a+b<=c || b+c<=a ||a+c<=b){//无法构成三角形的情况
            System.out.println(a +"," + b +"," +c +"的值无法构成三角形");
            return 0.0;
        }
        double p = (a + b + c) / 2;
       return Math.sqrt( p * (p-a) * (p-b) * (p-c));
    }

    /**
     * 主方法，Java程序的入口
     * @param args String[] 主方法的形参列表，它可以通过程序参数方式传入实参
     */
    public static void main(String[] args) {
        double base = 4;
        double height = 3;
        System.out.println("底边是4，高是3的三角形面积：" + triangleArea(base, height));

        double a = 3;
        double b = 4;
        double c = 5;
        System.out.println("底边分别为3,4,5的三角形面积：" + triangleArea(a,b,c));

        double x = 3;
        double y = 5;
        double z = 1;
        //违反三角形边长的要求：任意两边之和大于第三边，否则无法构成三角形
        System.out.println("底边分别为3,5,1的三角形面积：" + triangleArea(x,y,z));//NaN
    }
}

1.4 递归调用（难，可以暂时先放一放）

递归的难点在于你是否能通过数学知识找到某种规律。

递归的概念：一个方法自己调用自己。

如果递归没有用好，容易发生栈内存溢出错误。

使用递归：必须是有条件的递归，或者有出口的递归，即不能无限递归。

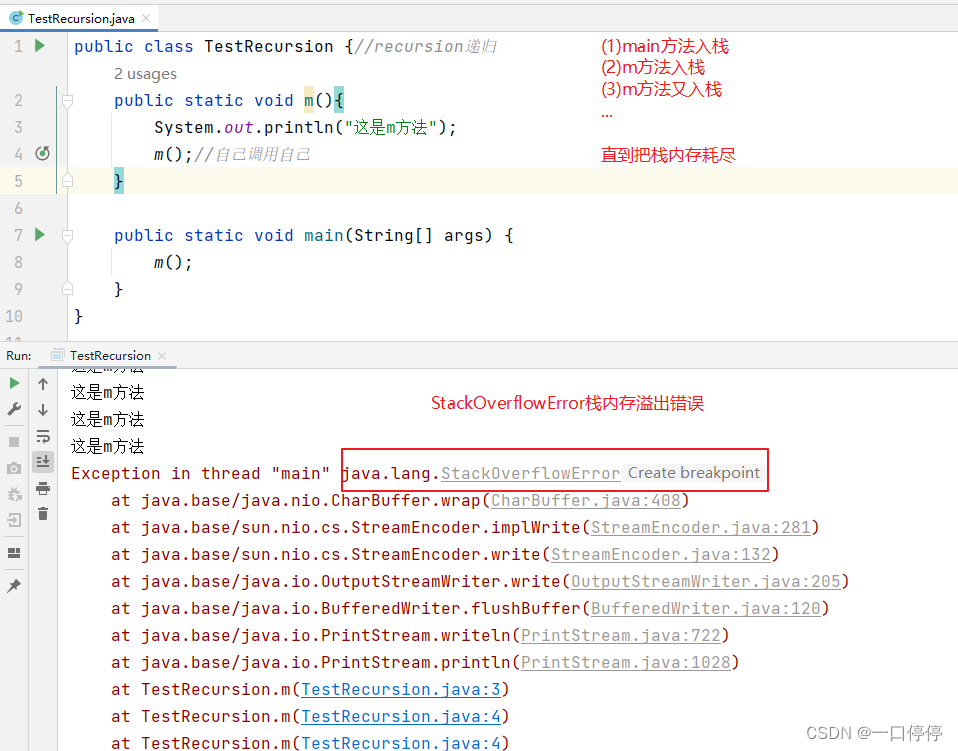
案例1：求n!

public class TestRecursion2 {
    public static void main(String[] args) {
        System.out.println(loopMethod(5));
        //5*4*3*2*1 = 120

        System.out.println(recursionMethod(5));

        System.out.println(recursionMethod(15));//1307674368000
    }

    /*
    //定义一个方法，求n!
    n！= n * (n-1)!

     */
    public static long recursionMethod(int n){
        if(n==1 || n==0){//1! 或 0! 就是1
            return 1;
        }
        return n * recursionMethod(n-1);
    }

    //定义一个方法，求n!
    /*
    用普通循环循环
    n! = 1*2*3*...*n
     */
    public static long loopMethod(int n){
        long result = 1;
        for(int i=1; i<=n; i++){
            result = result * i;
        }
        return result;
    }

}

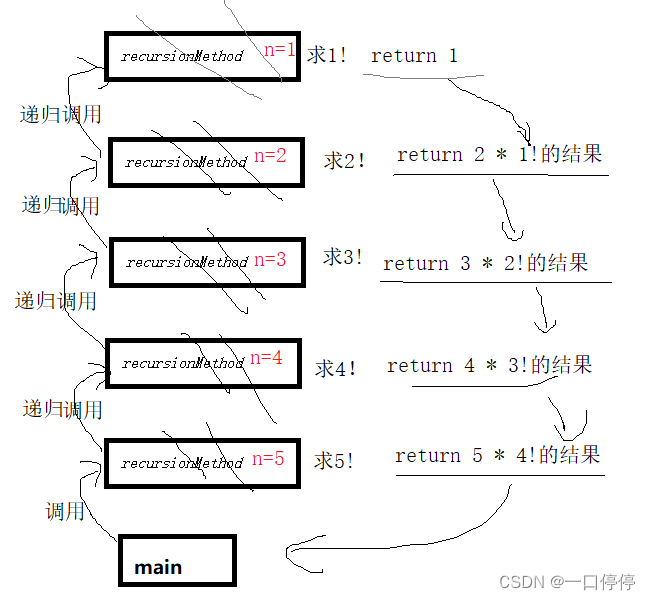
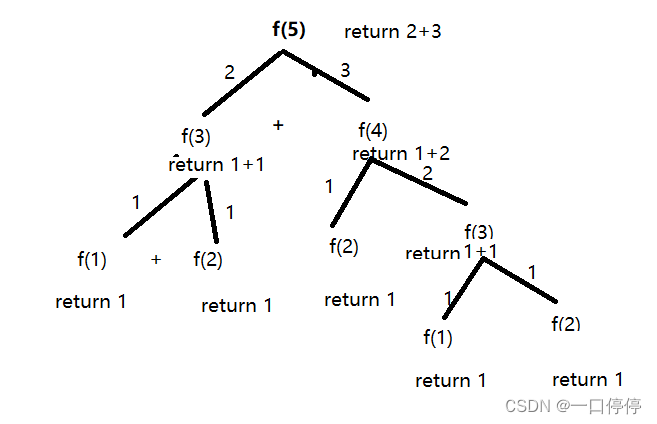
案例2：斐波那契数列

案例：计算斐波那契数列（Fibonacci）的第n个值，斐波那契数列满足如下规律，

1,1,2,3,5,8,13,21,....

即从第三个数开始，一个数等于前两个数之和。假设f(n)代表斐波那契数列的第n个值，那么f(n)满足：

f(n) = f(n-2) + f(n-1);

public class TestRecursion3 {
    public static void main(String[] args) {
        /*for(int i=1; i<=10; i++){
            System.out.print(loopFibonacci(i)+  "  ");
        }
        System.out.println();
        System.out.println("=================");
        for(int i=1; i<=10; i++){
            System.out.print(recursionFibonacci(i)+  "  ");
        }*/

        System.out.println(recursionFibonacci(5));
    }

    /*
    案例：计算斐波那契数列（Fibonacci）的第n个值，斐波那契数列满足如下规律，
        1,1,2,3,5,8,13,21,....
        即从第三个数开始，一个数等于前两个数之和。假设f(n)代表斐波那契数列的第n个值，那么f(n)满足：
        f(n) = f(n-2) + f(n-1);

        第1个数：1
        第2个数：1
        第3个数： 1    +    1    =   2
               bb     +    b    = current    bb：beforebefore，前前1个数  b:before：前一个数
        第4个数：1     +    2    =  3
                bb         b   =  current    bb就是上面一个b,  b就是上一个current
        第5个数：2     +    3     =5
               bb   +     b  =    current    bb就是上面一个b,  b就是上一个current

     */
    public static int loopFibonacci(int n){
        if(n==1 || n==2){
            return 1;
        }

        int bb = 1;
        int b = 1;
        int current = bb + b; //2
        /*
        假如 n=5
         i=4
            bb = b = 1;
            b = current = 2;
            current = bb + b = 1 +2 =3;
         i=5
            bb = b = 2;
            b = current = 3;
            current = bb + b = 2 + 3 = 5
         */
        for(int i=4; i<=n; i++){
            bb = b;
            b = current;
            current = bb + b;
        }
        return current;
    }

    /*
    案例：计算斐波那契数列（Fibonacci）的第n个值，斐波那契数列满足如下规律，
        1,1,2,3,5,8,13,21,....
        即从第三个数开始，一个数等于前两个数之和。假设f(n)代表斐波那契数列的第n个值，那么f(n)满足：
        f(n) = f(n-2) + f(n-1);
     */
    public static int recursionFibonacci(int n){
        if(n==1 || n==2){
            return 1;
        }
        return recursionFibonacci(n-2) + recursionFibonacci(n-1);
    }

}

练习题1：猴子吃桃

猴子吃桃子问题，猴子第一天摘下若干个桃子，当即吃了所有桃子的一半，还不过瘾，又多吃了一个。第二天又将仅剩下的桃子吃掉了一半，又多吃了一个。以后每天都吃了前一天剩下的一半多一个。到第十天，只剩下一个桃子。试求第一天共摘了多少桃子？

public class RecursionExercise10 {
    public static void main(String[] args) {
        for(int i=10; i>=1; i--){
//            System.out.println("第" +i +"天的桃子：" + peach(i));
            System.out.println("第" +i +"天的桃子：" + loop(i));
        }
    }

    /*
    猴子吃桃子问题，猴子第一天摘下若干个桃子，当即吃了所有桃子的一半，还不过瘾，又多吃了一个。
    第二天又将仅剩下的桃子吃掉了一半，又多吃了一个。
    以后每天都吃了前一天剩下的一半多一个。到第十天，只剩下一个桃子。试求第一天共摘了多少桃子？
    已知条件：
        第10天   剩1个桃子。                         peach(10)  = 1                        peach(day=10)
        第9天    ( 第10天桃子的数量 + 1 ) * 2        peach(9) = (peach(10) + 1 ) * 2        peach(day=9) = (peach(day+1) + 1)*2
        第8天    （第9天桃子的数量 + 1 ） * 2        peach(8) = (peach(9) + 1 ) * 2
        ...
        第1天    （第2天桃子的数量 + 1 ） * 2       peach(1) = (peach(2) + 1 ) * 2

        递归实现的方式
     */
    public static int peach(int day){
        if(day == 10){
            return 1;
        }
        return  (peach(day+1) + 1)*2;
    }

    public static int loop(int day){
        if(day == 10){
            return 1;
        }
        int sum  = 1;
        for(int i = 9; i>=day; i--){
            sum = (sum + 1)*2;
        }
        return sum;
    }
}

练习题2：走台阶

有n级台阶，一次只能上1步或2步，共有多少种走法？

public class RecursionExercise12 {
    public static void main(String[] args) {
        for(int i=1; i<=10; i++){
//            System.out.println("走到第" + i +"级台阶的总走法：" + f(i));
            System.out.println("走到第" + i +"级台阶的总走法：" + loop(i));
        }
    }

    //有n级台阶，一次只能上1步或2步，共有多少种走法？
    /*
    台阶的总数：          走法
       1                1
       2                11  2
       3                111 21  12
       4                1111  211  121   112 22
       5                11111  2111  1211   1121 221     1112   212  122
       假设 f(n)代表走到第n级台阶的总走法
          f(n) = f(n-1) + f(n-2)
     */
    public static int f(int n){
        if(n==1 ||  n==2){
            return n;
        }
        return f(n-1) + f(n-2);
    }

    public static int loop(int n){
        if(n==1 ||  n==2){
            return n;
        }
        //从第3级台阶开始
        int bb = 1;
        int b = 2;
        /*
        假设n=5
        i=3
           current = 1 + 2 = 3;
           bb = 2;
           b = 3;
        i=4
            current = 2 + 3 = 5;
            bb = 3;
            b = 5;
        i = 5
            current = 3 + 5 = 8;
            bb = 5;
            b = 8;
         */
        int current = 0;
        for(int i=3; i<=n; i++){
            current = bb + b;
            bb = b;
            b = current;
        }
        return current;
    }
}