算法设计与分析第三章：动态规划

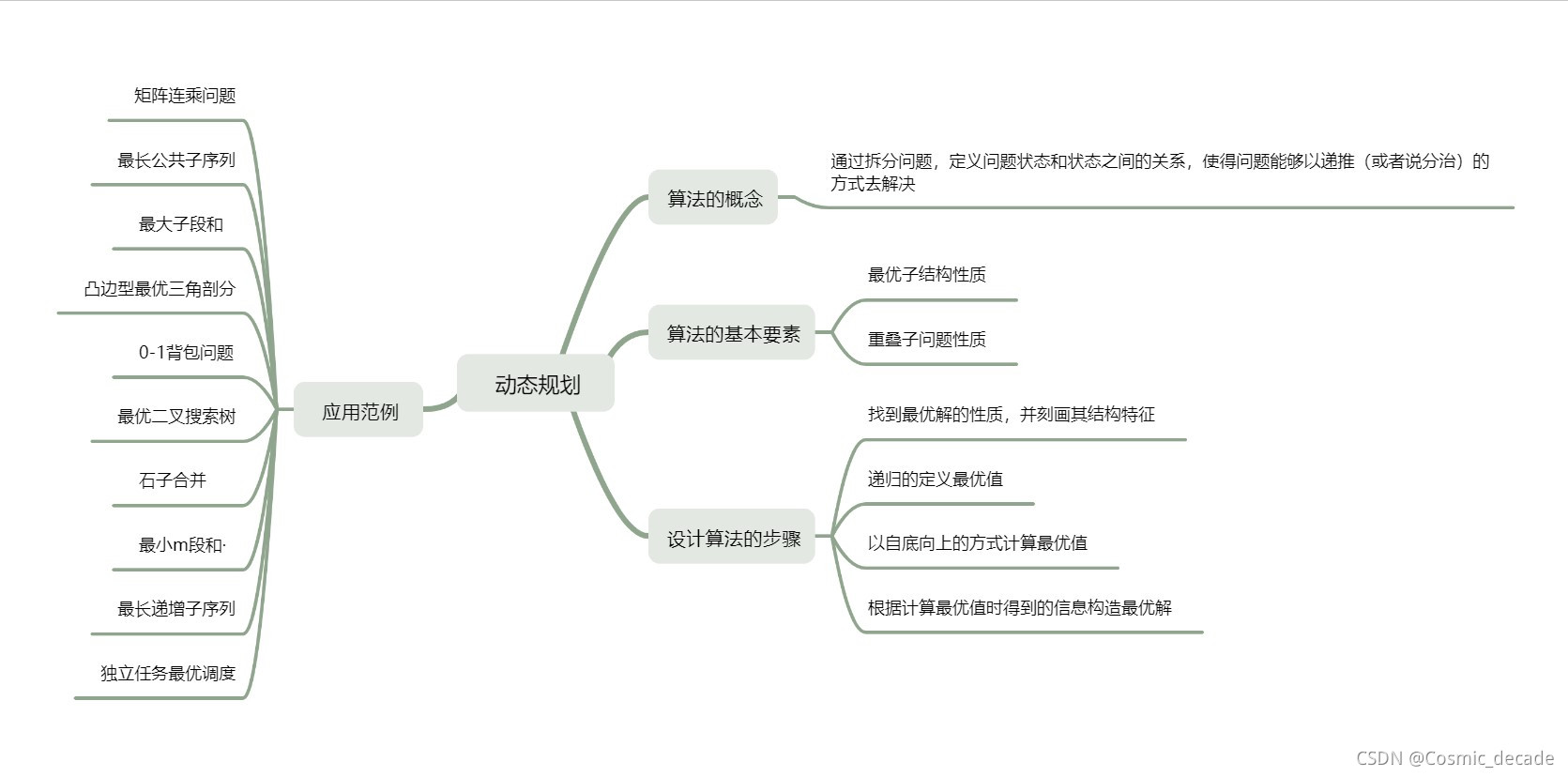
 最优子结构性质：如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。最优子结构性质为动态规划算法解决问题提供了重要线索。保证算法的正确性。

重叠子问题性质。重叠子问题性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的效率。

 应用范例

 矩阵连乘问题状态转移

这个问题的关键特征是：计算A[1:n]的最优次序所包含的矩阵子链A[1:k]和A[k+1:n]的次序也是最优的。我们可以反证来证明：如果A[1:n]的最优次序所包含的矩阵子链A[1:k]不是最优，那肯定有一个是比他次序少的，我们用其替换A[1:k]，所得的A[1:n]将比先前的更少，也就是说A[1:n]不是最有次序，矛盾

 状态转移方程：

stra[i][j]=0                                                                           i=j;

stra[i][j]=min(i<=k<j){stra[i][k]+stra[k+1][j]+p(i-1)*p(k)*p(j)} i<j.

物理意义：

stra[i][j]表示矩阵A[i]到A[j]的最少数乘次数。

最长公共子序列

状态转移方程：

c[i][j]=0                                 i>0;j = 0

c[i][j]=c[i-1][j-1]+1                 i,j>0;xi = yi

c[i][j]=max{c[i][j-1],c[i-1][j]}   i,j>0;xi != yi

物理意义：

c[i][j]记录序列X前i位和序列Y前j位的最长公共子序列的长度。

最大子段和

状态转移方程：

dp[i]=max(dp[i-1]+a[i],a[i])      1<=i<=n

物理意义：

dp[i]表示前i和数的最大字段和

凸边型最优三角剖分

与矩阵连乘相似

状态转移方程：

dp[i][j]=0                                                                           i=j;

dp[i][j]=min(i<=k<j){dp[i][k]+dp[k+1][j]+w((vi-1)(vk)v(j))}   i<j.

物理意义：

dp[i][j](1<=i<j<=n）为子凸多边形((vi-1)(vi)...(vj) 的 最 优 三 角 剖 分 对 应 的 最 优 值 的最优三角剖分对应的最优值 的最优三角剖分对应的最优值
 

0-1背包问题

状态转移方程：

dp[i][j]=dp[i-1][j]                                        j<w[i]

dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])     j>=w[i]

物理意义：

dp[i][j]表示前i个物品容量为j时的最大价值

w[i]第i个物品的大小/体积

v[i]第i个物品的价值

最优二叉搜索树

状态转移方程：

e[i][j]=q i-1                                          j=i-1

e[i][j]=min(i<=r<=j){e[i][r-1]+e[r+1][j]+w(i,j) }      i<=j

物理意义：

qi为虚拟键闸查找概率

定义e[i,j]为包含关键字ki,...,kj的最优二叉查找树的期望代价。

对一棵关键字ki,...,kj的子树，定义其概率总和为：w(i,j)

带虚拟键最优二叉树详解

石子合并

n堆石子，可以化成n条直线问题，取最小值即可。下面就是对于每一条直线问题，我们如何解决。第一点，我们要明确这条直线是从哪里开始的；第二点，我们要明确直线包括了哪些石子。即起点和长度。针对第二种问题，我们可以用起点到终点来表示，但是对于环形而言，直线就转化为0->4, 1->0, 2->1, 3->2, 4->3，用数组不好表示。对于起点和长度，我们可以用二维数组，两个坐标分别表示起点和长度。比如dp[1][5]表示从编号为1的石堆开始，合并从1开始的5个石堆所需要的最小花费。

状态转移方程：

dp[i][n]=0                                      n=1;

dp[i][n]=min(dp[i][k]+dp[(i+k)%n][n-k]+getSum(i,n))  1<=k<=n

物理意义：

dp[i][n]是指从i起的n堆石子，dp[i][k]是从i起的k堆，k到k+1为间断点，还剩下n - k堆，是从编号为(i + k) % n的石堆开始的，合并这两堆的费用是getSum(i, n)。步长为1时，花费为0。从步长为2开始，对于每条直线，计算dp[i][n]的最值，直到n == N（总共的堆数）。dp[i][N]的最小值即为所求。

最小m段和

状态转移方程：

dp[i][j]=dp[i-1][j]+a[i]                                                                                        j=1

dp[i][j]=dp[i][j] = MIN(for(k=1; k<=i; k++)MAX(dp[k][j-1], dp[i][1] - dp[k][1]))    j>1

物理意义：

用dp[i][j]存储长度为i，分j段后其子序列和的最大值的最小值，这当中k表示的是分段的最后一段子序列的开始下标，所以dp[k][j-1]是前面j-1段子序列和的最大值的最小值，dp[i][1] - dp[k][1]是最后一段子序列的和。所以取这两段中的最大值，在k值变化过程中取得到的最小值。

最长递增子序列

状态转移方程：

dp[i]=1,    i为第一个字符的角标（0或1）

dp[i]=max(dp[i],dp[j]+1)      j<i;s[j]<s[i]

物理意义：

从左到右依次考虑，每遇到一个点就从第一位开始遍历到该点，看以这个点作为前缀是否为最大值。dp[i]表示以第i个字符结尾的最大递增子序列的长度.

优化

只管维持一个最小的递增子序列即可。End数组存最小递增子序列，遍历字符串，如果字符ch[i]比end数组的最后一个字符大，则添加至end数组后，计数加一；否则在end数组二分查找第一个大于等于ch[i]的字符，将其替换。遍历完后，计数器的值即为最优解。

独立任务最优调度

状态转移方程：

dp[i][j]=dp[i-1][j]+b[i]                                    other

dp[i][j]=min(dp[i-1][j-a[i]],dp[i-1][j]+b[i])        a[i]<=j<=sum[a[1..i]]

物理意义：

dp[i-1][j]+b[i]表示第i个作业A机器不去做，交给B机器做，B处理的时间；而dp[i-1][j-a[i]表示作业i由机器A处理，B不需要管，所以B机器处理的时间就是上一个作业的处理时间，即为dp[i-1][j-a[i]]。

又完成任务最短时间应该由A机器完成时间和B机器完成时间中最大的那一个决定。因为一项任务真正的完工需要等待两个同时完工才算完成。

我们可以明确了，在确定B机器处理时间时，我们会取最小值；当计算作业完成时间时，我们要取A、B中的最大值，最后还要取最小值才表示完成作业的最短时间(这里取的最小值是分配问题，即作业由A机器处理的时间会产生不同，我们先算出A处理所用的总时间，在这个时间范围内进行遍历，所有分配种类中取最小。)最优解为n个作业，所有分配情况，每个情况取A、B机器所用时间的较大值，再在所有较大值中取最小值，即为最优。