如何理解高斯过程（二）：代码篇-CSDN博客

本文链接：https://blog.csdn.net/m0_50908842/article/details/147470448

源代码是类封装的，在学习过程中为了更好的步步推导，进行拆分

train_X = np.array([3, 1, 4, 5, 9]).reshape(-1, 1)
train_y = y(train_X, noise_sigma=1e-4)
test_X = np.arange(0, 10, 0.1).reshape(-1, 1)

数学原理：

从上式中，可以得到，我们需要三个核矩阵的计算

先从高斯核原理出发，给出相应的代码，再详细给出三个核矩阵依次的计算方式

高斯核函数

$K_{i}(x_{i},y_{i})=\exp(-\frac{||x_{i}-y_{i}||^2}{2\sigma^{2}_{i}})$

易混淆的点：train_x不能看成一个向量，而是每个点都是独立的。

对于向量而言：

将train_x每个点都看成独立的：

计算一：

dist_matrix[i][j] = np.sum((x1[i] - x2[j]) ** 2)

计算二：

 dist_matrix = np.sum(x1**2, 1).reshape(-1, 1) + np.sum(x2**2, 1) - 2 * np.dot(x1, x2.T)

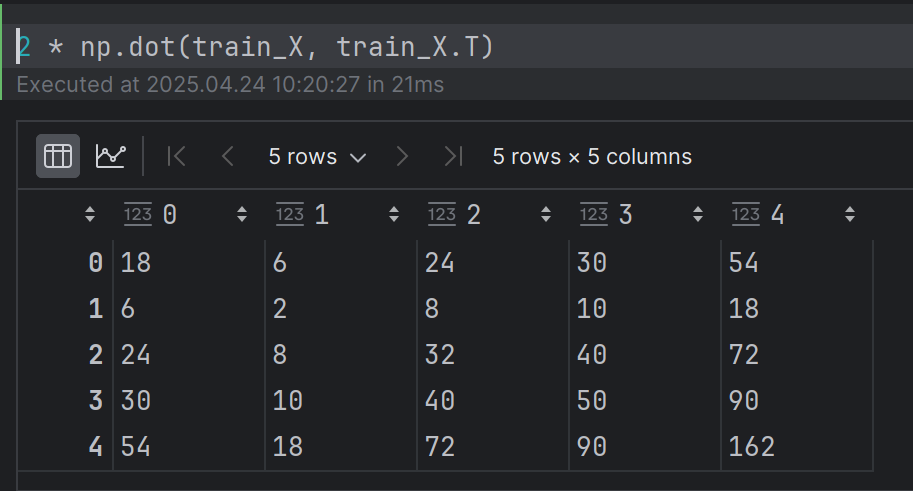
再带入指数计算

下面给出 Kyy 和 Kfy的计算过程

Kyy

Kfy

Kff_inv = np.linalg.inv(Kff + 1e-8 * np.eye(len(train_X)))  # (N, N)
mu = Kfy.T.dot(Kff_inv).dot(train_y)
cov = Kyy - Kfy.T.dot(Kff_inv).dot(Kfy)

新点就是1

1对应的输出值是0.54这是已经采集到，验证高斯过程是否能保证对已知点的验证能力

结果：mu接近真实值，sigma很小

为什么呢？

$\mu=K_{fy}^TK_{ff}^{-1}y$

$\sigma=K_{yy}-K_{fy}^{T}K_{ff}^{-1}K_{fy}$

其中 Kff不变， Kyy=1

由于测试点是1 ，从Kfy中可以看到和test_x的第二项一致，Kfy(2)=1

Kfy^{T}*Kff^{-1}y 会近似成[0 1 0 0 0]，从而得到结果和y的第二项接近。

且方差较小

高斯过程：当测试点接近训练点时候，对应的输出也会靠近训练点的输出，且方差较小