统计学习笔记3：k近邻算法及其python代码实现

本文链接：https://blog.csdn.net/m0_50947149/article/details/134620052

1 k近邻模型

就像近朱者赤近墨者黑的思想一样，在k近邻算法中给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的k个实例，这k个实例的多数属于某个类，就把该输入实例分为这个类。训练k近邻模型需要确定以下三个因素：①距离的计算。②k值的选择。③损失函数。

1.1 距离的计算

特征空间中两个实例点的距离是两个实例点相似程度的反映。特征空间中 $x_i$ , $x_j$ 的 $L_p$ 距离定义为

$L_p\left( x_i,x_j \right) =\left( \sum_{l=1}^n{\left| x_{i}^{\left( l \right)}-x_{j}^{\left( l \right)} \right|}^p \right) ^{\frac{1}{p}}$

其中n表示实例点的特征数。当p=1时称为曼哈顿距离，当p=2时称为欧式距离，当p= $\infty$ 时，它是各个坐标距离的最大值。

下图给出了二维空间中p取不同值时，与原点的 $L_p$ 距离为1（ $L_p=1$ ）的点的图形

由图形可知，不同的距离度量方式所确定的最近邻点是不一样的，而在k近邻算法中通常选择欧式距离作为距离的计算方式。

1.2 k值的选择

选择较小的k值会使模型的泛化能力变差，预测结果会对近邻实例点非常敏感，但假设邻近的实例点正好是噪声点，预测就会出现很大的误差，总的来说，k值减小意味着整体的模型变得复杂，容易发生过拟合现象。

选择较大的k值，就相当于用较大领域中的训练实例进行预测，这时与输入实例较远的训练实例也会对预测起作用，使预测发生错误，k值的增大意味着整体模型变得简单，故容易发生欠拟合的现象。

k值一般取一个比较小的数值，通常使用交叉验证法来选取最优的k值。

1.3 分类决策规则

k近邻法中的分类规则往往是多数表决，即由输入实例的k个邻近的训练实例中的多数类决定输入实例的类。假设分类的损失函数为0-1损失函数，分类函数为

$f:R^n\rightarrow \left\{ c_1,c_2,\cdots ,c_K \right\}$

那么误分类的概率是

$P\left( Y\ne f\left( X \right) \right) =1-P\left( Y=f\left( X \right) \right)$

对给定的实例x，其最近邻的k个训练实例点构成集合 $N_k(x)$ 。如果涵盖 $N_k(x)$ 的区域的类别是 $c_j$ ，那么误分类率是

$\frac{1}{k}\sum_{x_i\in N_k\left( x \right)}{I\left( y_i\ne c_j \right)}=1-\frac{1}{k}\sum_{x_i\in N_k\left( x \right)}{I\left( y_i=c_j \right)}$

要使误分类率最小即经验风险最小，所以多数表决规则等价于经验风险最小化。

2 k近邻法的实现：kd树

实现k近邻法时，主要考虑的问题是如何对训练数据进行快速k近邻搜索，最简单的实现方法是计算输入实例与每一个训练实例的距离，但当特征空间的维数大及训练数据容量大时，计算就会变得非常耗时，于是考虑使用特殊的结构存储训练数据，书中介绍的是一种名为kd树的方法。

2.1 构造kd树

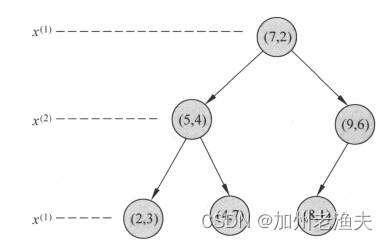
kd树实际上是一种二叉树，通常我们依次选择坐标轴将k维空间数据集切分，选择训练实例点在选定坐标轴上的中位数为切分点，这样得到的kd树称为平衡kd树。以书中例3.2所给数据集为例，构造kd树一般经过以下几个步骤：

给定一个二维空间的数据集：

$T=\left\{ \left( 2,3 \right) ^T,\left( 5,4 \right) ^T,\left( 9,6 \right) ^T,\left( 4,7 \right) ^T,\left( 8,1 \right) ^T,\left( 7,2 \right) ^T \right\}$

构造一个平衡kd树。

（1）构造根节点

选择 $x^{\left( 1 \right)}$ 为坐标轴，以所有实例点的 $x^{\left( 1 \right)}$ 坐标的中位数为根节点。由根节点生成深度为1的左右子节点，左子节点对应坐标 $x^{\left( 1 \right)}$ 小于切分点的子区域，右子节点对应坐标 $x^{\left( 1 \right)}$ 大于切分点的子区域。本例中将各个实例点按照横坐标排序，得到的中位数应该是 $(5+7)/2=6$ ，但由于没有横坐标为6的实例点，故取根节点为(7,2)。

（2）重复上述操作

对深度为j的节点，选择 $x^{\left( l \right)}$ 为切分的坐标轴， $l=j (mod\ k)+1$ ，以该节点的区域中所有实例的 $x^{\left( l \right)}$ 坐标的中位数为切分点，将该节点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴 $x^{\left( l \right)}$ 垂直的超平面实现。在本例中切分过程如下图所示

将横坐标小于7的实例点依据纵坐标排序求得中位数为4，故深度1的左叶子节点为(5,4)；同样将横坐标大于7的实例点依据纵坐标排序得到深度1的右叶子节点为(9,6)；深度2的叶子节点的划分依据则为横坐标，重复上述步骤，可得父节点为(5,4)的左叶子节点为(2,3)，右叶子节点为(4,7)；父节点为(9,6)的左叶子节点为(8,1)

（3）停止条件

当两个子区域没有实例存在时就停止划分，从而实现kd树的区域划分。本例中最终的划分结果如下图所示。

2.2 搜索kd树

利用kd树可以省去对大部分数据点的搜索，从而减少搜索的计算量，下面是搜索kd树的步骤：

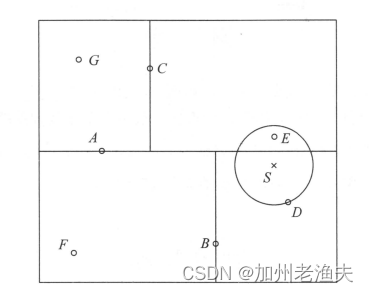
假设有下图所示的训练数据空间，S为输入目标实例点，求S的最近邻。

根据上图，我们可以先构造出kd树如下图所示：

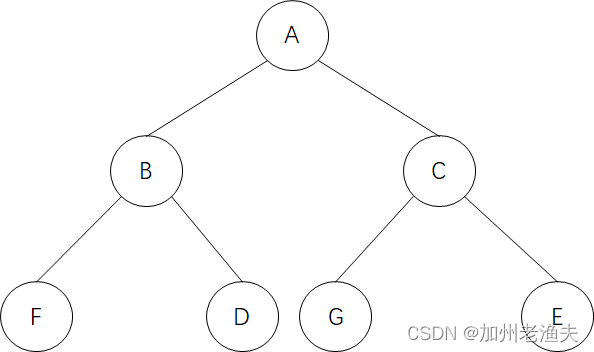
第一步：从根节点出发，递归地向下访问kd树，若是实例点S的坐标在当前切分的坐标轴处的坐标小于切分点，则向左访问，反之，向右访问，直到访问到叶节点，取该叶节点作为包含S的节点。本例中根节点为A，显然S的纵坐标小于A，故向左访问子节点B；S的横坐标大于B，故向右访问子节点D，而D已经是叶子节点，故选取D作为包含S的叶节点，即当前最近点。

第二步：向前回溯。从当前最近点回退该点所属的父节点，访问父节点的另一个分支，查看该子空间是否与超球体相交，即检查是否有节点比当前最近点与S距离更近。若有，则选择该点作为新的当前最近点，若没有，则回退kd树上一层的父节点。在上图中，回退D的父节点B，检查节点B的另一个子节点F，F距离更远，退回父节点A，检查A是另一个子节点C的区域，发现点E在圆内，且比D更近，设置E为新的当前最近点。

第三步：回退到根节点，搜索结束，当前最近点即为最近邻点。图中，回退C的父节点A，即根节点，搜索结束，最近邻点为E。

3 k近邻法的python代码实现

以《统计学习方法》书中的例3.2给出的数据为例，给定一个二维空间的数据集：

$T=\left\{ \left( 2,3 \right) ^T,\left( 5,4 \right) ^T,\left( 9,6 \right) ^T,\left( 4,7 \right) ^T,\left( 8,1 \right) ^T,\left( 7,2 \right) ^T \right\}$

确定(3,4.5)的最近邻点。

3.1构造kd树

以前文所述的方法对数据集按照不同坐标轴依次切分，得到存储该训练数据集的kd树，代码如下：

#此方法用于记录节点，data用于存储节点的数据，left用来存储左子节点的引用，right用于存储右子节点的引用。
class Node:  
    def __init__(self,data,left=None,right=None):
        self.val=data
        self.left=left
        self.right=right

class KdTree:
    def __init__(self,k):
        self.k=k                         #坐标的维数

    def create_Tree(self,dataset,depth):
        if not  dataset:
            return  None            #若是数据集中没有数据则说明切分完毕
        mid_index=len(dataset)//2   #计算中间位置
        axis=depth%self.k           #由于索引下标从0开始，故此处不用+1
        sort_dataset=sorted(dataset,key=(lambda x:x[axis])) #以axis为键对数据进行排序
        mid_data=sort_dataset[mid_index] #记录中位数
        cur_node=Node(mid_data)          #将中位数记录为切分点
        left_data=sort_dataset[:mid_index] #在axis轴上小于切分点的为左子树
        right_data=sort_dataset[mid_index+1:] #在axis轴大于切分点的为右子树
        cur_node.left=self.create_Tree(left_data,depth+1) #对左子树进行深层的切分操作
        cur_node.right=self.create_Tree(right_data,depth+1)#对右子树进行深层的切分操作
        return cur_node

3.2 搜索kd树

在创建完kd树后，就要对输入实例点的最近邻点进行搜索。首先需要找到包含输入实例点的叶子节点，找到叶子节点后再后退回父节点看看是否有比该叶子节点更近的实例点，直到退回到根节点。代码如下所示：

    def search(self,tree,new_data):
        self.near_point=None
        self.near_val=None

        def dfs(node,depth):
            if not node:
                return         #没有节点说明已经到达叶子节点
            axis=depth%self.k  #由于此处索引从0开始，故不用+1
            if new_data[axis]<node.val[axis]: #输入实例点若在axis轴上小于切分点
                dfs(node.left,depth+1)        #搜索左子树，深度+1
            else:
                dfs(node.right,depth+1)       #反之搜索右子树，深度+1

            dist=self.distance(new_data,node.val)  #计算叶子节点和输入实例点的距离
            if not self.near_val or dist<self.near_val: #找到更近的邻点
                self.near_val=dist     #更新距离
                self.near_point=node.val #更新邻点位置

            if abs(new_data[axis]-node.val[axis])<=self.near_val: 
                if new_data[axis]<node.val[axis]:
                    dfs(node.right,depth+1)  #原本搜索叶子节点去的左子树现在搜索右子树
                else:
                    dfs(node.left,depth+1)   #原本搜索右子树的现在搜索左子树
        dfs(tree,0) #从根节点开始对kd树进行搜索
        return self.near_point #输出最近邻点
    #用于求两点之间的欧式距离 
    def distance(self,point_1,point_2):
        res=0
        for i in range(self.k):
            res+=(point_1[i]-point_2[i])**2  
        return res**0.5

3.3可视化

把所有实例点绘制在一幅图中，并将输入实例点与其最近邻点相连，代码如下：

    x_values=[x[0] for x in data_set]
    y_values=[x[1] for x in data_set]
    plt.title('Kd tree for KNN')
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.scatter(x_values,y_values,color='b')
    plt.scatter(new_data[0],new_data[1],color='r')
    plt.plot([predict[0],new_data[0]],[predict[1],new_data[1]],color='g')
    plt.show()

3.4 整体代码

实现最近邻点搜索的整体代码如下：

import matplotlib.pyplot as plt

#该方法包含三个参数：data用来存储节点的数据，left用来存储左子节点的引用，默认为None，right用来存储右子节点的引用，默认也为None。
# 这样定义的初始化方法使得我们可以在创建Node对象时，通过传入数据和可选的左右子节点来初始化节点。
class Node:
    def __init__(self,data,left=None,right=None):
        self.val=data
        self.left=left
        self.right=right

class KdTree:
    def __init__(self,k):
        self.k=k                         #坐标的维数

    def create_Tree(self,dataset,depth):
        if not  dataset:
            return  None            #若是数据集中没有数据则说明切分完毕
        mid_index=len(dataset)//2   #计算中间位置
        axis=depth%self.k           #由于索引下标从0开始，故此处不用+1
        sort_dataset=sorted(dataset,key=(lambda x:x[axis])) #以axis为键对数据进行排序
        mid_data=sort_dataset[mid_index] #记录中位数
        cur_node=Node(mid_data)          #将中位数记录为切分点
        left_data=sort_dataset[:mid_index] #在axis轴上小于切分点的为左子树
        right_data=sort_dataset[mid_index+1:] #在axis轴大于切分点的为右子树
        cur_node.left=self.create_Tree(left_data,depth+1) #对左子树进行深层的切分操作
        cur_node.right=self.create_Tree(right_data,depth+1)#对右子树进行深层的切分操作
        return cur_node

    def search(self, tree, new_data):
        self.near_point = None
        self.near_val = None

        def dfs(node, depth):
            if not node:
                return  # 没有节点说明已经到达叶子节点
            axis = depth % self.k  # 由于此处索引从0开始，故不用+1
            if new_data[axis] < node.val[axis]:  # 输入实例点若在axis轴上小于切分点
                dfs(node.left, depth + 1)  # 搜索左子树，深度+1
            else:
                dfs(node.right, depth + 1)  # 反之搜索右子树，深度+1

            dist = self.distance(new_data, node.val)  # 计算叶子节点和输入实例点的距离
            if not self.near_val or dist < self.near_val:  # 找到更近的邻点
                self.near_val = dist  # 更新距离
                self.near_point = node.val  # 更新邻点位置

            if abs(new_data[axis] - node.val[axis]) <= self.near_val:
                if new_data[axis] < node.val[axis]:
                    dfs(node.right, depth + 1)  # 原本搜索叶子节点去的左子树现在搜索右子树
                else:
                    dfs(node.left, depth + 1)  # 原本搜索右子树的现在搜索左子树

        dfs(tree, 0)  # 从根节点开始对kd树进行搜索
        return self.near_point  # 输出最近邻点
        # 用于求两点之间的欧式距离

    def distance(self, point_1, point_2):
        res = 0
        for i in range(self.k):
            res += (point_1[i] - point_2[i]) ** 2
        return res ** 0.5


if __name__=='__main__':
    data_set=[[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]
    k=len(data_set[0])
    new_data=[3,4.5]
    kd_tree=KdTree(k)
    out_tree=kd_tree.create_Tree(data_set,0)
    predict=kd_tree.search(out_tree,new_data)
    print('Nearest Point of {}: {}'.format(new_data,predict))

    x_values=[x[0] for x in data_set]
    y_values=[x[1] for x in data_set]
    plt.title('Kd tree for KNN')
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.scatter(x_values,y_values,color='b')
    plt.scatter(new_data[0],new_data[1],color='r')
    plt.plot([predict[0],new_data[0]],[predict[1],new_data[1]],color='g')
    plt.show()

运行上述程序后，输出如下：