算法学习之路ACWING——前缀和、差分

        前缀和与差分是两种用于高区间查询和效处理数组修改的算法技巧，前缀和通过预处理快速计算区间和，差分通过记录变化点实现批量修改。

        也就是说前缀是用来快速求出某段区间的和，差分是可以批量修改某段区间的值。

前缀和

一维前缀和

原理 pre[ i ] = pre [ i - 1 ] + nums [ i ] ;

        其中pre数组中每一个当前pre[ i ]存放的是给定数组nums中第一个数nums[1]到当前下标 i 对应的nums[i] 的总和。

        由上述原理可以知道 求区间L，R之间的前缀和对应公式为 pre[ r ] - pre[ l - 1], 由此得出L， R 之间所有数的和。

#include <stdio.h>

int N = 1e5 + 7;

int main(){
    int n, m, l, r;
    
    int nums[N], pre[N];
      scanf("%d %d",&n, &m);
    for(int i = 1; i <= n; i++){
        scanf("%d", &nums[i]);
        pre[i] = pre[i - 1] + nums[i]; 
    }
    

    for(int i = 1; i <= m; i++){
       scanf("%d%d", &l, &r);
       printf("%d\n", pre[r] - pre[l - 1]);
    }
    
}

   二维数组的前缀和

给出一个二维数组，在给出一个子数组的左上角坐标、右下角坐标，求出子数组中的所有元素的和。这里S为前缀和数组，A存放数组元素。

如图所示，让我们求的是绿方块中所有数的和。也就是说对于每一个S[i][j], 表示的是以A[i][j]为右下角的矩阵中所有数的和。

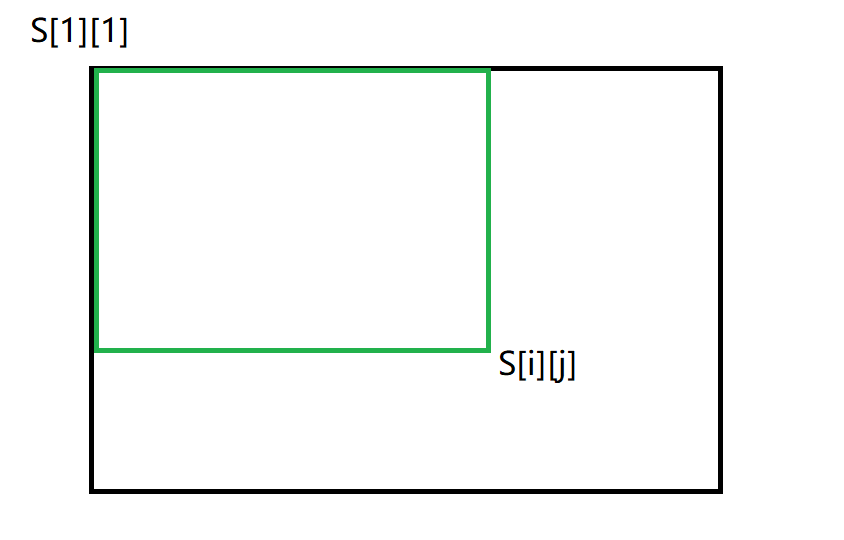
        如何求S[i] [j]

        S[1][1] = A[1][1]

        S[1][2] = A[1][1] + A[1][2] 

                    = S[1][1] + A[1][2]

        

        S[1][3] = A[1][1] + A[1][2]  + A[1][3]

                    = S[1][2] + A[1][3]

        

        S[2][1] = a[1][1] + a[2][1] 

                    = S[1][1] + a[2][1]

        

        S[2][2] = a[1][1] + a[1][2] + a[2][1] + a[2][2]

                    = S[1][2] + S[2][1] - S[1][1] + a[2][2]

        S[2][3] = A[1][1] + A[1][2] + A[1][3] + A[2][1] + A[2][2] + A[2][3] 
                    = S[1][3] + S[2][2] - S[1][2] + A[2][3] 

可以得到一下公式：

S[ i ][ j ] = S[ i -1][ j ] + S[ i ][ j - 1] - S[ i - 1][ j - 1] + A[ i ] [ j ]; 

也就是，可以在𝑜(𝑛2)的时间复杂度内求出所有s.

  

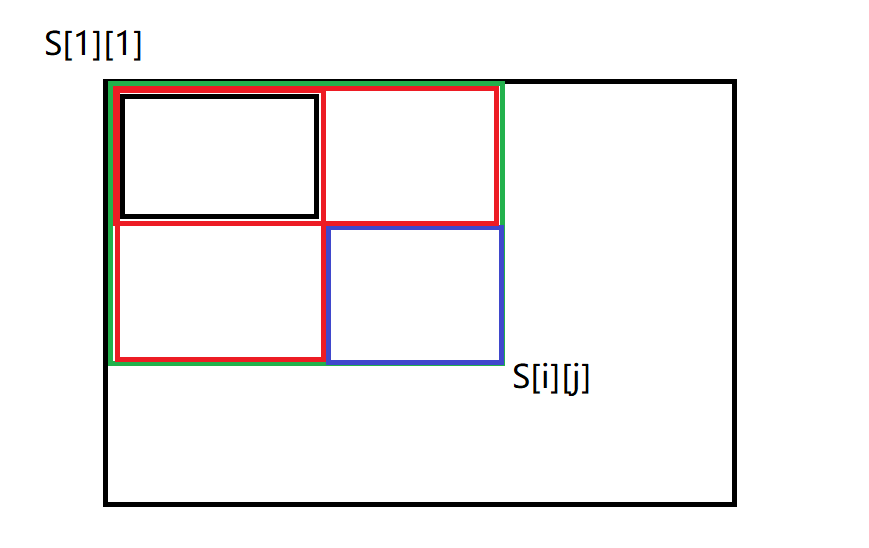
如图所示： 蓝色框内和 = 绿色框 - 红色框 1- 红色框 2 + 黑色框

也就是 (x1,y1) ~ (x2, y2)的和 = S[ x2][ y2] - S[x2][ y1 - 1] - S[x1 - 1][y2] + S[ x1 - 1][ y1 -1] 

#include <stdio.h>
int N = 1e3 + 7;

int main(){
    int num[N][N], S[N][N];
    int n, m, q;
    scanf("%d %d %d", &n, &m, &q);
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            scanf("%d", &num[i][j]);
            S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j -1] + num[i][j];
        }
    }
    
    
    int x1, y1, x2, y2;
    for(int i = 0; i < q; i++){
        int res;
        scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
        res = S[x2][y2] - S[x2][y1 - 1] - S[x1 - 1][y2] + S[x1 - 1][y1 - 1];
        printf("%d\n", res);
    }
}

差分

一维差分

差分可以看成前缀和的逆运算

差分数组：

 首先给定一个原数组 a: a[1] , a[2], a[3] ...... a[n];

 然后构造一个数组b：b[1], b[2], b[3] ...... b[n];

使得a[ i ]  = b[1] + b[2] + ...... + b[ i ];

也就是说数组a是数组b的前缀和数组， 反过来我们把b数组叫做a数组的差分数组。

考虑如何构造b数组？

        以下方法最直接：

        b[0] = 0;

        b[1] = a[ 1 ] - a[ 0 ];

        b[ 2 ] = a[ 2 ] - a[ 1];

        b [ 3 ] = a[3] - a[ 2 ];

        ......

        b[N] = a[N] - a[N - 1]

我们只要有数组b，通过前缀和运算，就能在O(n)时间得到数组a；

知道了差分数组有什么用呢？有下面这么一个问题：

给定区间[l ,r ]，让我们把a数组中的[ l, r]区间中的每一个数都加上c,即 a[l] + c , a[l+1] + c , a[l+2] + c ,,,,,, a[r] + c;

        暴力做法是for循环l到r区间，时间复杂度O(n)，如果我们需要对原数组执行m次这样的操作，时间复杂度就会变成O(n*m)。有没有更高效的做法吗? 考虑差分做法。

        始终要记得，a数组是b数组的前缀和数组，比如对b数组的b[i]的修改，会影响到a数组中从a[i]及往后的每一个数。

        首先让差分b数组中的 b[l] + c ,a数组变成 a[l] + c ,a[l+1] + c,,,,,, a[n] + c;

        然后我们打个补丁，b[r+1] - c, a数组变成 a[r+1] - c,a[r+2] - c,,,,,,,a[n] - c;

        为什么还要打个补丁？

        我们画个图理解一下这个公式的由来:

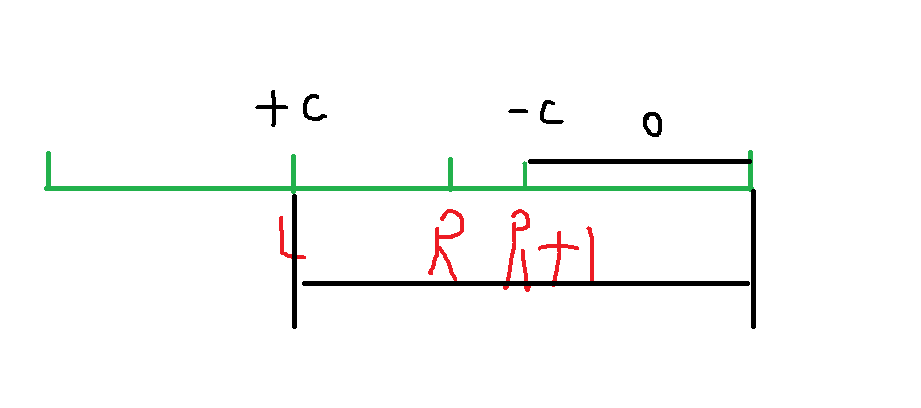
        b[l] + c，使得a数组中 a[l]及以后的数都加上了c(绿线下面黑色部分)，但我们只要求l到r区间加上c, 因此还需要执行 b[r+1] - c,让a数组中a[r+1]及往后的区间再减去c(绿线上面黑色部分)，这样对于a[r] 以后区间的数相当于没有发生改变。

        因此我们得出一维差分结论：给a数组中的[ l, r]区间中的每一个数都加上c,只需对差分数组b做 b[l] + = c, b[r+1] - = c。时间复杂度为O(1), 大大提高了效率。

总结 一维差分：对a数组 [l ，r]区间的每一个数加上c ： b[l] + c, b[r+ 1] - c

//差分 时间复杂度 o(m)
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        b[i] = a[i] - a[i - 1];      //构建差分数组
    }
    int l, r, c;
    while (m--)
    {
        scanf("%d%d%d", &l, &r, &c);
        b[l] += c;     //将序列中[l, r]之间的每个数都加上c
        b[r + 1] -= c;
    }
    for (int i = 1; i <= n; i++)
    {
        a[i] = b[i] + a[i - 1];    //前缀和运算
        printf("%d ", a[i]);
    }
    return 0;
}

差分矩阵

对于差分矩阵我们来画个图理解一下：

整个a数组

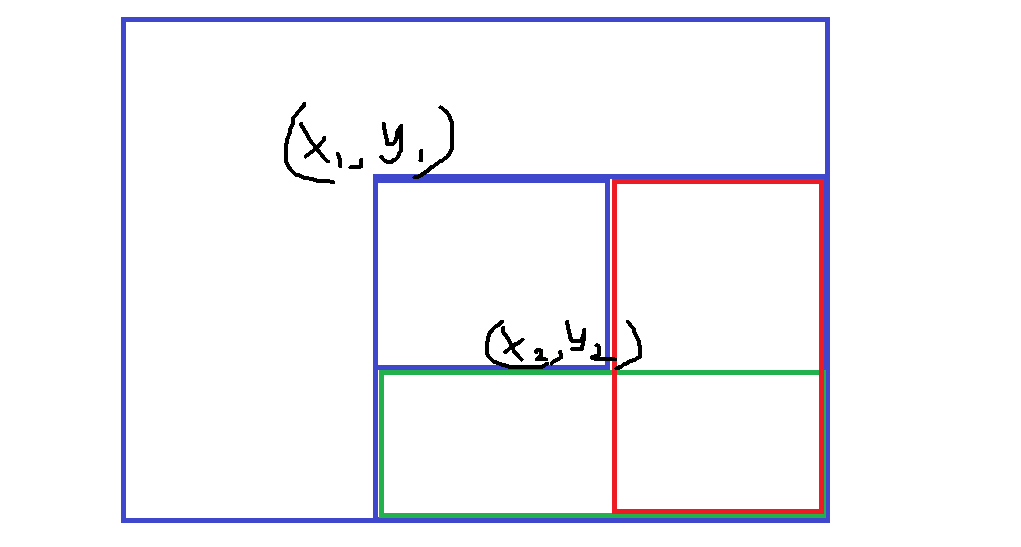差分b数组：

        b[x1][y1] += c;

        b[x2 + 1][y1] -= c;

        b[x1][y2 + 1] -= c;

        b[x2+1][y2 + 1] +=c;        

#include <stdio.h>
int N = 1e3 + 5;
int n, m, k;

void insert(int l1, int r1, int l2, int r2, int c, int (*p)[N]){
    
    p[l1][r1] += c;
    p[l2 + 1][r1] -= c;
    p[l1][r2 + 1] -= c;
    p[l2 + 1][r2 + 1] += c;
}

int main(){
    
 
    int p[N][N], q[N][N];
    scanf("%d %d %d", &n, &m, &k);
    for(int  i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
             scanf("%d",&q[i][j]); 
        }
    }
    
    for(int  i = 1; i <= n; i++){
        for(int  j = 1; j <= m; j++){
            insert(i, j, i, j, q[i][j], p);
        }
    }
    
    while(k--){
        int x1, x2, y1, y2, c;
        scanf("%d %d %d %d",&x1, &y1, &x2, &y2, &c);
        insert(x1 , y1, x2, y2, c, p);
    }
    
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            p[i][j] = p[i - 1][j] + p[i][j - 1] - p[i - 1][j - 1] + p[i][j];
            printf("%d ", p[i][j]);
        }
        
        printf("\n");
    }
}