图--建立----12月8日

图

1.表示

用邻接矩阵表示：
带权的图用无穷大初始化矩阵
—意思:顶点不可到达，
但是自己可以到达自己，距离是0 。
不带权的图用0 就可以。

上面的查找顶点用散列改进比较好。

邻接矩阵的用法：

无向图：

邻接表：

这里默认A,B,C,D都是起点

与其他点邻接，则拓展一个单链表。
### 二、有向图的邻接表

这里是分为正向和逆向的邻接表

### 三、网络带权图的连接表

这里讲第三种的具体代码实现

第一步：
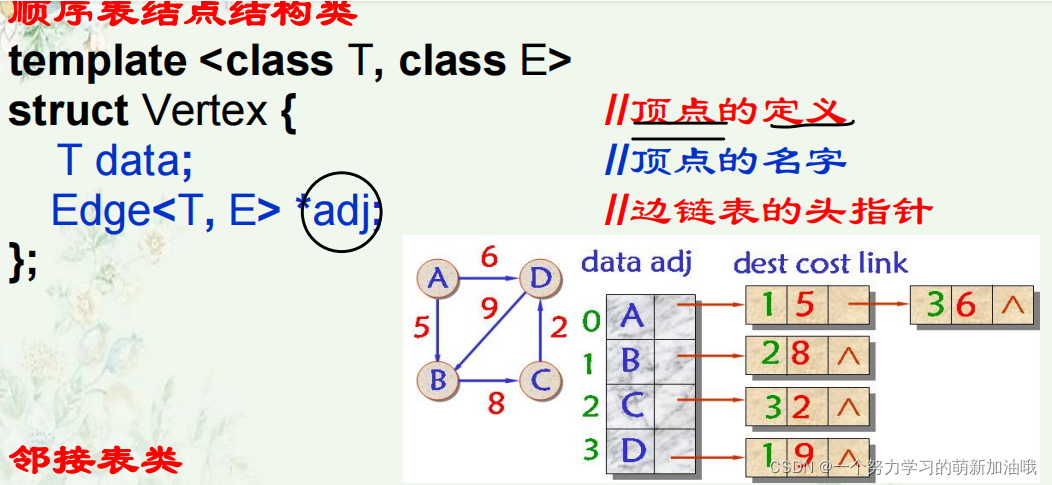
1.构建结点（ 存相邻的结点 （包括位置下标 ， 权重 ， 指针域 ） ）

2.构建类（就是单链表的类）
包括指针域和数据域。

指针指向的结点类型是 Edge ( 边结点类型 )

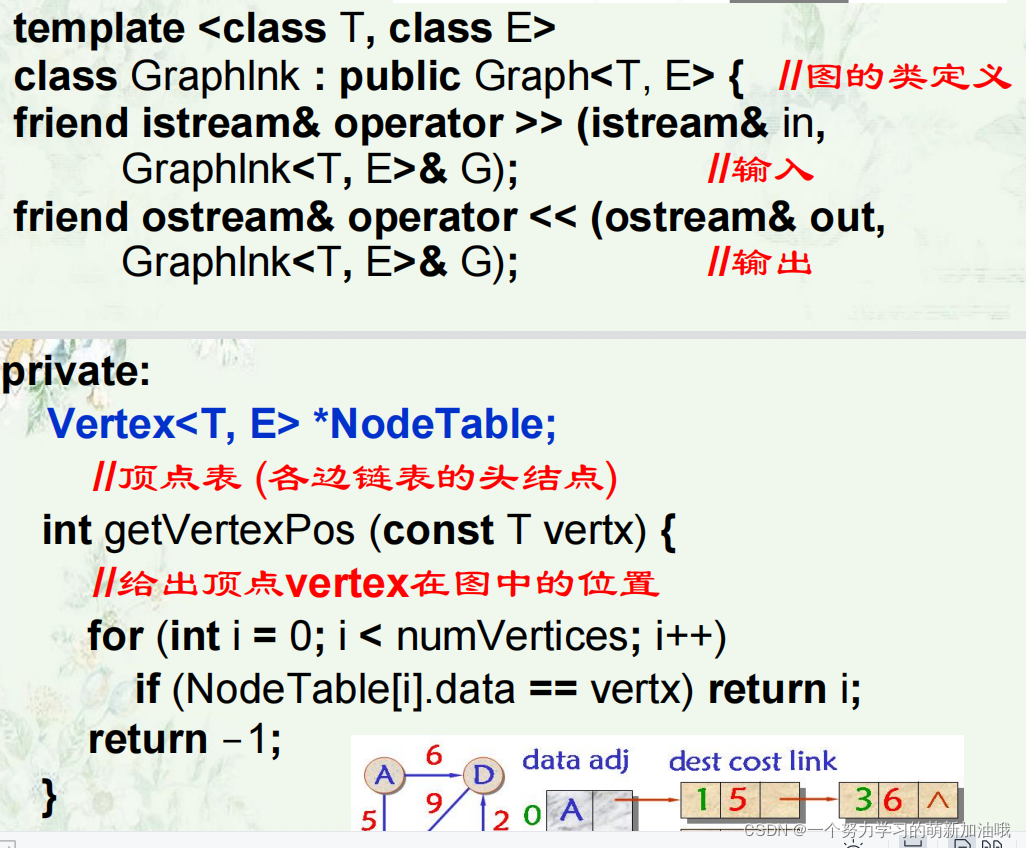
顶点表、

有头指针、
data域是存该结点的值，比如图中的 A , B ,C ，D 等。

析构需要先析构链表，再析构数组

=====================

下面是创建

完整代码：

#pragma once
#include<iostream>
using namespace std;
//图的邻接表结构
const int DefaultVertices = 30;//默认最大顶点数
//边结点
template<class T>//T为顶点名字
struct Edge {
	int dest;//边的另一个顶点的位置
	int cost;//边上的权值
	Edge<T>* link;//这个点的下一条边
	Edge() { dest = -1; cost = 0; link = NULL; }
    Edge(int num, int weight) { dest = num; cost = weight; link = NULL; }
};

//顶点
template<class T>//T为数据
struct Vertex {
	T data;//顶点名字
	Edge<T>* adj;//边链表的头指针
};

//图
template<class T>//T为顶点名字
class Graph {
public:
	int maxVertices;//图中最大顶点数
	int numEdges;//当前边数
	int numVertices;//当前顶点数
	Vertex<T>* NodeTable;//顶点表(各边链表的头指针)
    int getVertexPos(T vetrex) {//给出顶点vetrex在图中的位置
        for (int i = 0; i < numVertices; i++) {
            if (NodeTable[i].data == Vertex)return i;
        }
        return -1;
    }
    Graph(int sz = DefaultVertices) {//初始化
        maxVertices = sz; numVertices = 0; numEdges = 0;
        NodeTable = new Vertex<T>[maxVertices];//创建顶点表数组
        for (int i = 0; i < maxVertices; i++) {
            NodeTable[i].adj = NULL;//边链表头指针赋空
        }
    }
    ~Graph() { delete[]NodeTable; }

    //图输入
    friend istream& operator>>(istream& in, Graph<T>& G) {
        int n,v1pos, v2pos;//序号
        T v1, v2; int w;
        cout << "请输入序号选择图的类型：1.无向图  2.有向图" << endl;
        in >> n;//输入序号
        switch (n) {
        case 1:
            cout << "请输入无向图的顶点总数："; in >> G.numVertices;
            while (G.numVertices > G.maxVertices || G.numVertices < 0) {
                cout << "顶点总数不能超过30个，也不能是负数，请重新输入："; in >> G.numVertices;
            }
            cout << "请输入各顶点的名字：" << endl;
            for (int i = 0; i < G.numVertices; i++) {
                in >> G.NodeTable[i].data;
            }
            cout << "请输入边的总数："; in >> G.numEdges;
            while (G.numVertices < 0) {
                cout << "边的总不能是负数，请重新输入："; in >> G.numEdges;
            }
            cout << "请输入各边连接的两个顶点：" << endl;
            for (int i = 0; i < G.numEdges; i++) {
                int f = 0;
                in >> v1 >> v2;
                for (int j = 0; j < G.numVertices; j++) {
                    //判断输入顶点是否在图内
                    if (v1 == G.NodeTable[j].data) {
                        f++; v1pos = j;//记录顶点在顶点表的位置
                    }
                    if (v2 == G.NodeTable[j].data) {
                        f++; v2pos = j;
                    }
                    if (f == 2)break;
                }
                if (f < 2) {
                    cout << "有顶点不存在图内，请重新输入两个顶点和边的权值：";
                    i--;
                }
                else {
                    Edge<T>* p = G.NodeTable[v1pos].adj;
                    //v1顶点添加边
                    if (p == NULL) {//该顶点还没有边时
                        p = new Edge<T>;//创建边
                        G.NodeTable[v1pos].adj = p;//p为边链表的头结点
                    }
                    else {
                        while (p->link != NULL)p = p->link;//来到最后一个结点
                        Edge<T>* t = new Edge<T>;//创建边 
                        p->link = t;
                        p = t;
                    }
                    p->dest = v2pos;//边的另一个顶点的位置
                    //p->cost = w;//边的权值
                    p->link = NULL;//下一条边赋值为空

                    //v2顶点添加边
                    p = G.NodeTable[v2pos].adj;
                    if (p == NULL) {//该顶点还没有边时
                        p = new Edge<T>;//创建边
                        G.NodeTable[v2pos].adj = p;//p为边链表的头结点
                    }
                    else {
                        while (p->link != NULL)p = p->link;//来到最后一个结点
                        Edge<T>* t = new Edge<T>;//创建边 
                        p->link = t;
                        p = t;
                    }
                    p->dest = v1pos;//边的另一个顶点的位置
                    //p->cost = w;//边的权值
                    p->link = NULL;//下一条边赋值为空
                }
            }
            break;
        case 2:
            cout << "请输入有向图的顶点总数："; in >> G.numVertices;
            while (G.numVertices > G.maxVertices || G.numVertices < 0) {
                cout << "顶点总数不能超过30个，也不能是负数，请重新输入："; in >> G.numVertices;
            }
            cout << "请输入各顶点的名字：" << endl;
            for (int i = 0; i < G.numVertices; i++) {
                in >> G.NodeTable[i].data;
            }
            cout << "请输入边的总数："; in >> G.numEdges;
            while (G.numVertices < 0) {
                cout << "边的总不能是负数，请重新输入："; in >> G.numEdges;
            }
            cout << "请输入各边连接的始顶点、终顶点："<<endl;
           
            for (int i = 0; i < G.numEdges; i++) {
                int f = 0;
                in >> v1 >> v2;
                for (int j = 0; j < G.numVertices; j++) {
                    //判断输入顶点是否在图内
                    if (v1 == G.NodeTable[j].data) {
                        f++; v1pos = j;//记录顶点在顶点表的位置
                    }
                    if (v2 == G.NodeTable[j].data) {
                        f++; v2pos = j;
                    }
                    if (f == 2)break;
                }
                if (f < 2) {
                    cout << "有顶点不存在图内，请重新输入两个顶点和边的权值：";
                    i--;
                }
                else {
                    Edge<T>* p = G.NodeTable[v1pos].adj;
                    //v1始顶点添加边
                    if (p == NULL) {//该顶点还没有边时
                        p = new Edge<T>;//创建边
                        G.NodeTable[v1pos].adj = p;//p为边链表的头结点
                    }
                    else {
                        while (p->link != NULL)p = p->link;//来到最后一个结点
                        Edge<T>* t = new Edge<T>;//创建边 
                        p->link = t;
                        p = t;
                    }
                    p->dest = v2pos;//边的终顶点的位置
                   // p->cost = w;//边的权值
                    p->link = NULL;//下一条边赋值为空
                    
                }
            }
            break;
        default:cout << "序号输入错误！" << endl;
        }
        return in;
    }

    //图的输出
    friend ostream& operator<<(ostream& out, Graph<T>& G) {
        cout << "顶点集合：" << endl;
        for (int i = 0; i < G.numVertices;i++) {
            cout << G.NodeTable[i].data << ' ';
        }
        cout << endl << "边集合：" << endl;
        for (int i = 0; i < G.numVertices;i++) {
            Edge<T>* p = G.NodeTable[i].adj;
            if (p != NULL) {//顶点有边时
                cout << "与" << G.NodeTable[i].data << "相连的边有：";
                while (p != NULL) {
                    cout << "(" << G.NodeTable[i].data << "," << G.NodeTable[p->dest].data << ")  ";
                    p = p->link;

                }
                cout << endl;
            }
            
        }
        return out;
    }

    //u的第一个邻接顶点的位置
    int getFirstNeigbor(int u) {
        if (u<0 || u>=numVertices)return -1;
        if (NodeTable[u].adj != NULL)return NodeTable[u].adj->dest;
        else return -1;
    }

    //v的邻接顶点w的下一个邻接顶点的位置
    int getNextNeigbor(int v, int w) {
        if (v >= 0 && v < numVertices) {
            Edge<T>* p = NodeTable[v].adj;
            //寻找w
            while (p != NULL && p->dest != w) p = p->link;
            if (p != NULL && p->link != NULL)return p->link->dest;//找到
        }
        return -1;//没找到
    }

    void PrintPath(int u, int v, bool* visited,int* path,int pLen) {
        int w;
        visited[u] = 1;//记录u被访问，防止死循环
        pLen++; path[pLen] = u;//路径长度++,顶点u加入到路径中
        if (u == v&&pLen>0) {//找到一条u->v的路径
            for (int i = 0; i < pLen; i++) {
                cout << NodeTable[path[i]].data << "->";
            }
            cout << NodeTable[path[pLen]].data << endl;
            return;//找到一条路径之后返回
        }
        w = getFirstNeigbor(u);//第一个邻接顶点的位置
        while (w != -1) {//w存在
            //如果w未被访问过，递归访问w
            if (!visited[w]) {
                PrintPath(w, v, visited, path, pLen);
                visited[w] = 0;//回退之后要重置
            }  
            //当w被访问过，且w是终点，且路径>0，说明路径构成回路
            else if (w == v && pLen > 0) {//打印回路
                for (int i = 0; i <= pLen; i++) {
                    cout << NodeTable[path[i]].data << "->";
                }
                cout << NodeTable[w].data << endl;
            }
            w = getNextNeigbor(u, w);//访问下一个邻接顶点
        }
    }
};

main.cpp

#include <iostream>
#include "Graph.h"
using namespace std;
void hasFalse(bool* visited,int size) {
	for (int i = 0; i < size; i++) {
		visited[i] = false;//数组初始化为false
	}
}
int main(int argc, char* argv[]) {
	Graph<char>G;
	cin >> G;//图的输入
	cout << G;//图的输出

	//求有向图的简单路径
	bool *visited=new bool[G.numVertices];//判断顶点是否已经被访问
	int* path = new int[G.numVertices];//顶点路径
	hasFalse(visited, G.numVertices);//数组初始化

	//打印第i个位置的顶点到第j个位置的顶点的路径
	cout << "该图的简单路径为：" << endl;
	for (int i = 0; i < G.numVertices; i++) {
		for (int j = 0; j < G.numVertices; j++) {
			if (i == j)continue;//回路不是简单路径，不打印
			else G.PrintPath(i, j, visited, path, -1);
			hasFalse(visited, G.numVertices);//数组初始化
		}
	}

	cout << endl<<"该图的简单回路有："<<endl;
	for (int i = 0; i < G.numVertices; i++) {
		hasFalse(visited, G.numVertices);//数组初始化
		G.PrintPath(i, i, visited, path, -1);
	}

	delete[]visited; delete[]path;
	return 0;
}
/*
6
A B C D E F
8
A F
A B
F B
B C
B E
C D
D E
C A
*/