动态规划---数位统计DP、状态压缩DP、树形DP、记忆化搜索

1.数位统计DP

1.1例题：计数问题

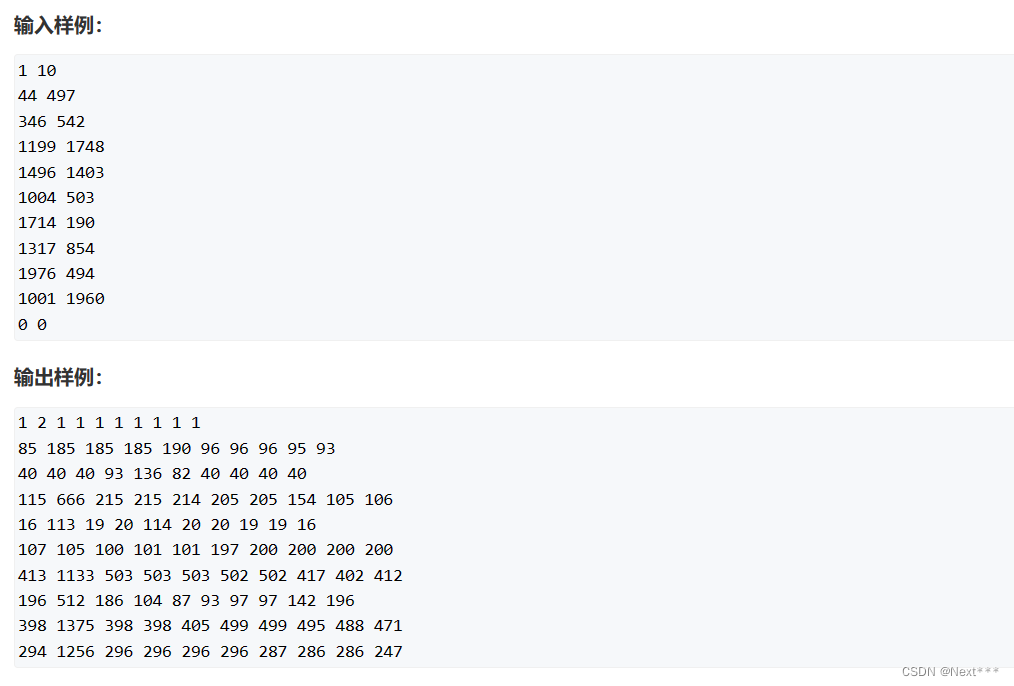
图示：

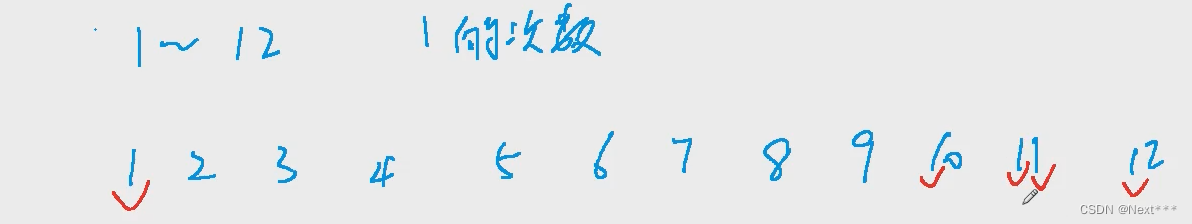
链接: 大佬写法

2.状态压缩DP

2.1蒙德里安的梦想

求把 $N\times M$ 的棋盘分割成若干个 $1\times 2$的长方形，有多少种方案。

例如当 $N=2，M=4$ 时，共有 $5$ 种方案。当 $N=2，M=3$ 时，共有 $3$ 种方案。

如下图所示：

输入格式
输入包含多组测试用例。

每组测试用例占一行，包含两个整数$N$ 和 $M$。

当输入用例 $N=0，M=0$ 时，表示输入终止，且该用例无需处理。

输出格式
每个测试用例输出一个结果，每个结果占一行。

数据范围
$1\le N,M\le 11$
输入样例：

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

输出样例：

1
0
1
2
3
5
144
51205

题解：

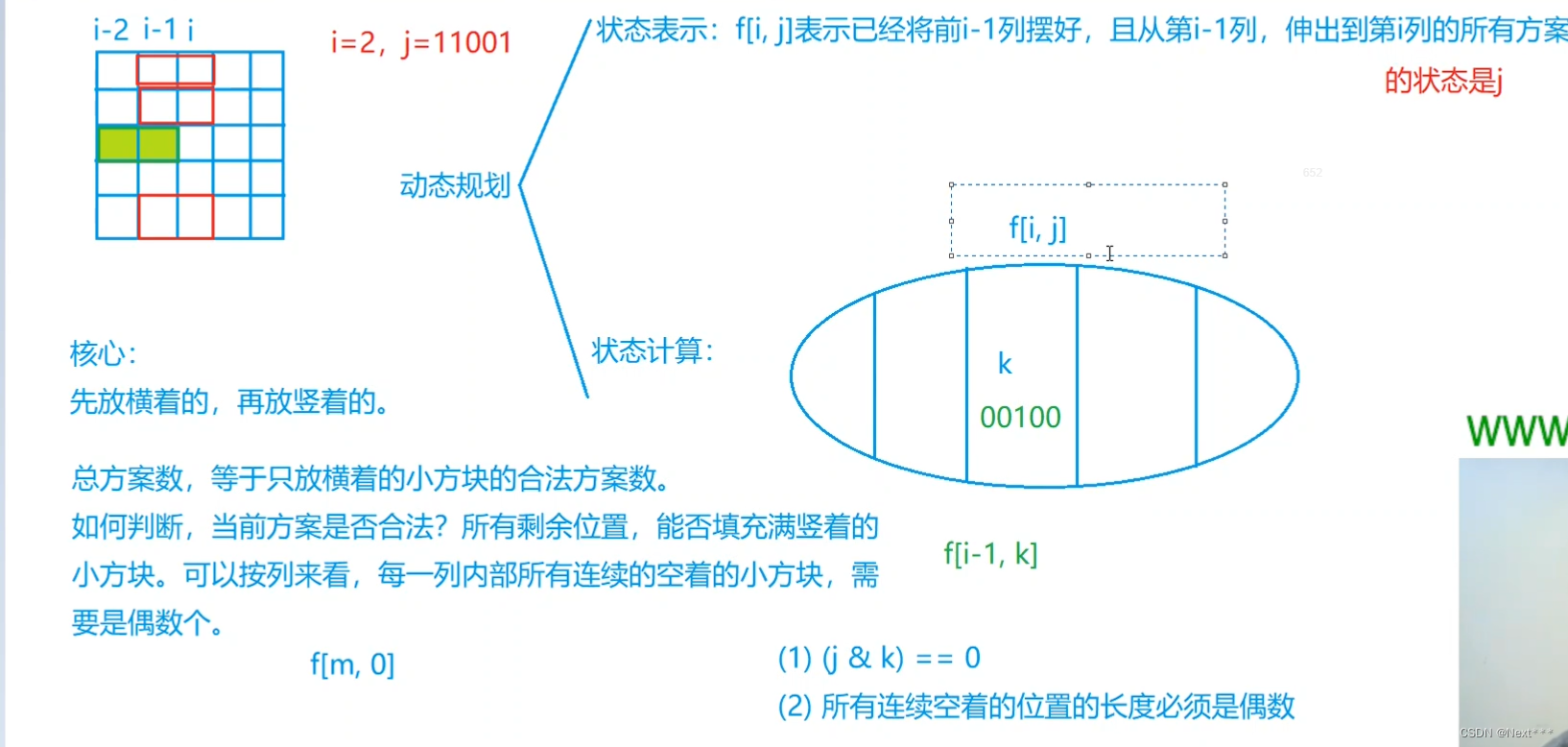
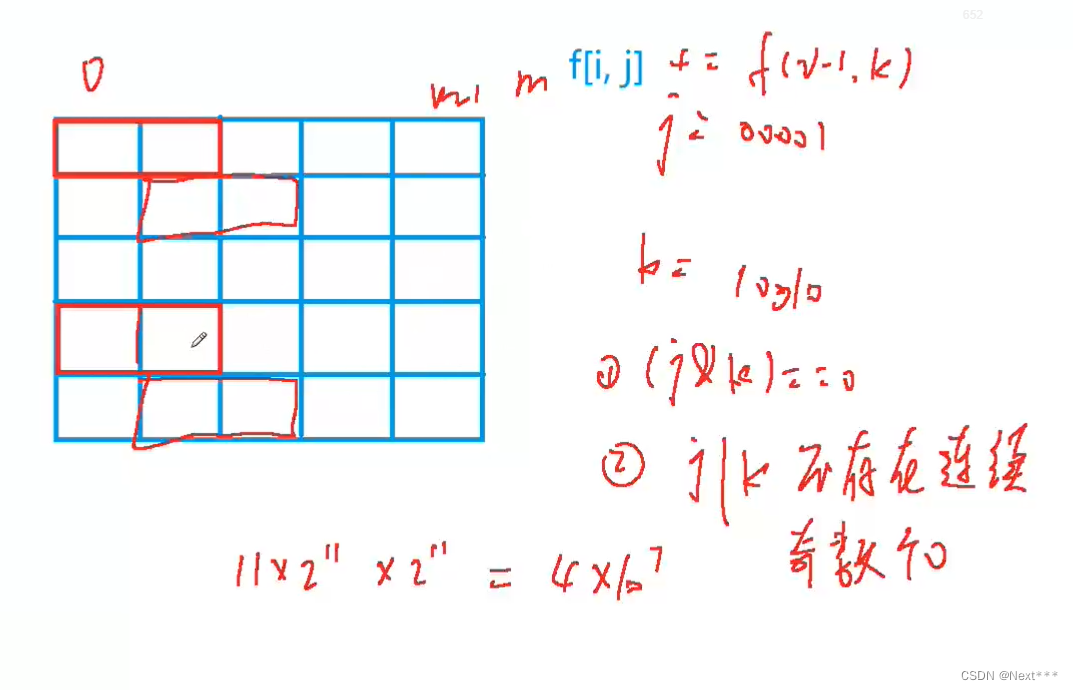
核心：
摆放的小方格方案数 等价于 横着摆放的小方格方案数
如何判断当前方案是否合法？
遍历每一列，i列的方案数只和i-1列有关系

• j&k==0， i-2列伸到i-1的小方格 和i-1列放置的小方格 不重复。
• 每一列，所有连续着空着的小方格必须是偶数个

dp分析：
状态表示 f[i][j]: 前i-1列已经确定，且从第i-1列伸出的小方格在第i列的状态为j 的方案数。属性：个数。

i=2, j=11001 表示下列图的状态

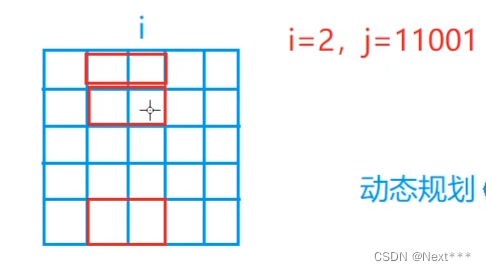
但是i-1, i列已经固定，所以集合划分是依据i-2 列伸到 i-1 列的不同状态 k 来划分

i-2 列伸到 i-1 列的状态 k=00100

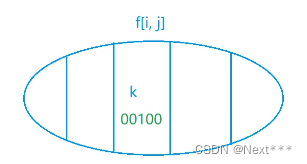
状态计算：（限制条件：i-1列非空白位置可以不能放置小方格），在i列不同的放置方法就是不同的集合划分。
问题：第 i-2 列伸到 i-1 列的状态为 k ， 是否能成功转移到 第 i-1 列伸到 i 列的状态为 j ?
需要满足如下条件:

• j&k==0， i-2列伸到i-1的小方格和i-1列放置的小方格 不重复。
• 每一列，所有连续着空着的小方格必须是偶数个
  f[m][0]:
  列数从0开始计数，m列不放小方格，前m-1列已经完全摆放好并且不伸出来的状态

#include<iostream>
#include<cstring>

using namespace std;

//数据范围1~11
const int N = 12;
//每一列的每一个空格有两种选择，放和不放，所以是2^n
const int M = 1 << N;
//方案数比较大，所以要使用long long 类型
//f[i][j]表示 i-1列的方案数已经确定，从i-1列伸出，并且第i列的状态是j的所有方案数
long long f[N][M];
//第 i-2 列伸到 i-1 列的状态为 k ， 是否能成功转移到 第 i-1 列伸到 i 列的状态为 j
//st[j|k]=true 表示能成功转移
bool st[M];
//n行m列
int n, m;

int main() {
//    预处理st数组
    while (cin >> n >> m, n || m)
    {
        for (int i = 0; i < 1 << n; i++) 
        {
//            第 i-2 列伸到 i-1 列的状态为 k ， 
//            能成功转移到 
//            第 i-1 列伸到 i 列的状态为 j
            st[i] = true;
//            记录一列中0的个数
            int cnt = 0;
            for (int j = 0; j < n; j++) 
            {
//                通过位操作，i状态下j行是否放置方格，
//                0就是不放， 1就是放
                if (i >> j & 1) 
                {
//                    如果放置小方块使得连续的空白格子数成为奇数，
//                    这样的状态就是不行的，
                    if (cnt & 1) 
                    {
                        st[i] = false;
                        break;
                    }
                }else cnt++;
//                不放置小方格
            }

            if (cnt & 1) st[i] = false;
        }

//        初始化状态数组f
        memset(f, 0, sizeof f);

//        棋盘是从第0列开始，没有-1列，所以第0列第0行，不会有延伸出来的小方块
//        没有横着摆放的小方块，所有小方块都是竖着摆放的，这种状态记录为一种方案
        f[0][0] = 1;
//        遍历每一列
        for (int i = 1; i <= m; i++) 
        {
//            枚举i列每一种状态
            for (int j = 0; j < 1 << n; j++) 
            {
//                枚举i-1列每一种状态
                for (int k = 0; k < 1 << n; k++) 
                {
//                    f[i-1][k] 成功转到 f[i][j]
                    if ((j & k) == 0 && st[j | k]) 
                    {
                        f[i][j] += f[i - 1][k]; //那么这种状态下它的方案数等于之前每种k状态数目的和
                    }
                }
            }
        }
//        棋盘一共有0~m-1列
//        f[i][j]表示 前i-1列的方案数已经确定，从i-1列伸出，并且第i列的状态是j的所有方案数
//        f[m][0]表示 前m-1列的方案数已经确定，从m-1列伸出，并且第m列的状态是0的所有方案数
//        也就是m列不放小方格，前m-1列已经完全摆放好并且不伸出来的状态
        cout << f[m][0] << endl;
    }
    return 0;
}

问题：蒙德里安的梦想，那里为啥要1<<12？
<<代表移位 移一位相当于2 两位4 移n位是*2^n
这代表的是状态,N可以代表行，M代表的是状态，f[N][M],有N行代表着有2^N种状态
比如是3行4列 则状态一共有 100 110 000 001 011 111 101 010 一共八种 也就是2^3 也就是1<<3

2.2最短Hamilton路径

给定一张 $n$ 个点的带权无向图，点从 $0\sim n-1$ 标号，求起点 $0$ 到终点 $n-1$ 的最短 $Hamilton$ 路径。

$Hamilton$ 路径的定义是从 $0$ 到 $n-1$ 不重不漏地经过每个点恰好一次。

输入格式
第一行输入整数 $n$。

接下来 $n$ 行每行 $n$ 个整数，其中第 $i$ 行第 $j$ 个整数表示点 i 到 j 的距离（记为 $a[i,j]$）。

对于任意的 $x,y,z$，数据保证 ￥a[x,x]=0，a[x,y]=a[y,x]$ 并且$a[x,y]+a[y,z]\ge a[x,z]$。

输出格式
输出一个整数，表示最短 $Hamilton$ 路径的长度。

数据范围
$1\le n\le 20$
$0\le a[i,j]\le 107$
输入样例：

5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0

输出样例：

18

图解




状态压缩DP分析:
1.本题思路
假设:一共有七个点,用0,1,2,3,4,5,6来表示,那么先假设终点就是5,在这里我们再假设还没有走到5这个点,且走到的终点是4,那么有以下六种情况:
first: 0–>1–>2–>3–>4 距离:21
second: 0–>1–>3–>2–>4 距离:23
third: 0–>2–>1–>3–>4 距离:17
fourth: 0–>2–>3–>1–>4 距离:20
fifth: 0–>3–>1–>2–>4 距离:15
sixth: 0–>3–>2–>1–>4 距离:18

如果此时你是一个商人你会走怎样的路径?显而易见,会走第五种情况对吧?因为每段路程的终点都是4,且每种方案的可供选择的点是0 ~ 4,而商人寻求的是走到5这个点的最短距离,而4到5的走法只有一种,所以我们选择第五种方案，可寻找到走到5这个点儿之前,且终点是4的方案的最短距离,此时0~5的最短距离为(15+4走到5的距离).(假设4–>5=8)

同理:假设还没有走到5这个点儿,且走到的终点是3,那么有一下六种情况:
first: 0–>1–>2–>4–>3 距离:27
second: 0–>1–>4–>2–>3 距离:22
third: 0–>2–>1–>4–>3 距离:19
fourth: 0–>2–>4–>1–>3 距离:24
fifth: 0–>4–>1–>2–>3 距离:26
sixth: 0–>4–>2–>1–>3 距离:17

此时我们可以果断的做出决定:走第六种方案!!!,而此时0~5的最短距离为(17+3走到5的距离)(假设3–>5=5)

在以上两大类情况之后我们可以得出当走到5时:
1.以4为终点的情况的最短距离是:15+8=23;
2.以3为终点的情况的最短距离是:17+5=22;
经过深思熟虑之后,商人决定走以3为终点的最短距离,此时更新最短距离为:22。

当然以此类推还会有以1为终点和以2为终点的情况,此时我们可以进行以上操作不断更新到5这个点的最短距离,最终可以得到走到5这个点儿的最短距离,然后再返回最初的假设,再依次假设1,2,3,4是终点,最后再不断更新,最终可以得出我们想要的答案

2.DP分析:
用二进制来表示要走的所以情况的路径,这里用i来代替
例如走0,1,2,4这三个点,则表示为:10111;
走0,2,3这三个点:1101;
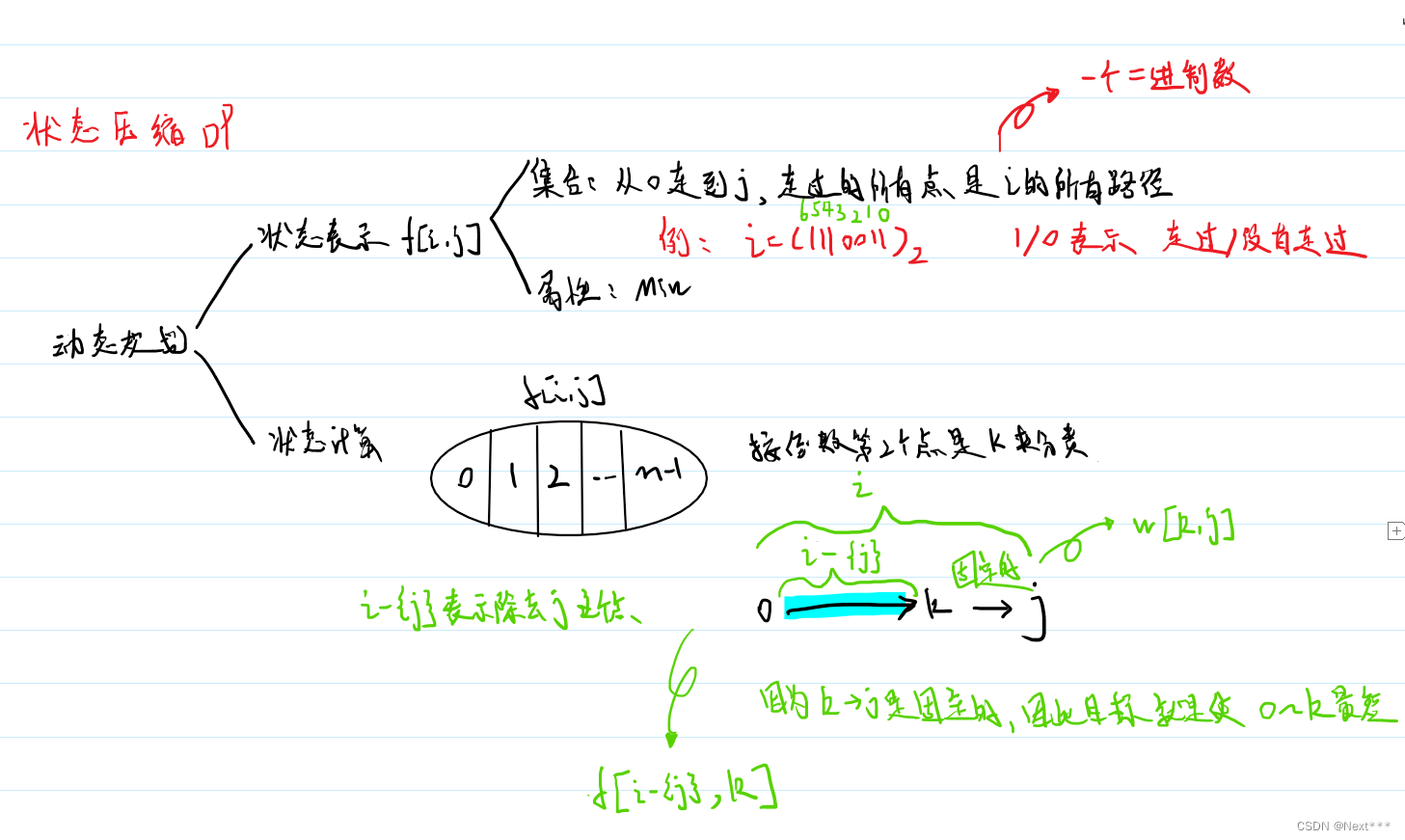
状态表示:f[i][j];
集合:所有从0走到j,走过的所有点的情况是i的所有路径
属性:MIN
状态计算:如1中分析一致,0–>·····–>k–>j中k的所有情况

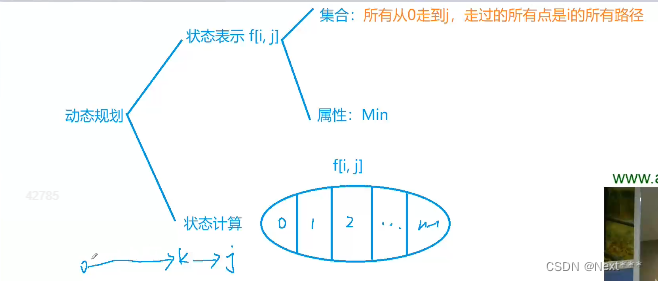
状态转移方程:f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j])

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N=20,M=1<<N;

int f[M][N],w[N][N];//w表示的是无权图

int main()
{
    int n;
    cin>>n;

    for(int i=0;i<n;i++)
     for(int j=0;j<n;j++)
      cin>>w[i][j];

    memset(f,0x3f,sizeof(f));//因为要求最小值，所以初始化为无穷大
    f[1][0]=0;//因为零是起点,所以f[1][0]=0;

    for(int i=0;i<1<<n;i++)//i表示所有的情况
     for(int j=0;j<n;j++)//j表示走到哪一个点
      if(i>>j&1)
       for(int k=0;k<n;k++)//k表示走到j这个点之前,以k为终点的最短距离
        if(i>>k&1)
         f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j]);//更新最短距离

    cout<<f[(1<<n)-1][n-1]<<endl;//表示所有点都走过了,且终点是n-1的最短距离
    //位运算的优先级低于'+'-'所以有必要的情况下要打括号
    return 0;
}

3.树形DP

3.1没有上司的舞会

Ural 大学有 $N$ 名职员，编号为 $1\sim N$。

他们的关系就像一棵以校长为根的树，父节点就是子节点的直接上司。

每个职员有一个快乐指数，用整数 $H_i$ 给出，其中 $1\le i\le N$。

现在要召开一场周年庆宴会，不过，没有职员愿意和直接上司一起参会。

在满足这个条件的前提下，主办方希望邀请一部分职员参会，使得所有参会职员的快乐指数总和最大，求这个最大值。

输入格式
第一行一个整数 $N$。

接下来 $N$ 行，第 $i$ 行表示 $i$ 号职员的快乐指数 $H_i$。

接下来 $N-1$ 行，每行输入一对整数 $L,K$，表示 $K$ 是 $L$ 的直接上司。

输出格式
输出最大的快乐指数。

数据范围
$1\le N\le 6000,$
$-128\le Hi\le 127$
输入样例：

7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5

输出样例：

5