2021.杭电中超第一场.补题

最新推荐文章于 2022-08-04 17:24:11 发布

Eter`nal

最新推荐文章于 2022-08-04 17:24:11 发布

阅读量180

点赞数 1

分类专栏：杭电文章标签：算法

本文链接：https://blog.csdn.net/m0_51488693/article/details/119319877

版权

杭电专栏收录该内容

5 篇文章 0 订阅

订阅专栏

1001 https://acm.hdu.edu.cn/showproblem.php?pid=6950 签到，打表找规律就好了。
1005 Minimum spanning tree https://acm.hdu.edu.cn/showproblem.php?pid=6954 思维题，签到

大意：现有 n 个点 (2<=n<=10000000)，任意两点a,b之间的之间的权重为 lcm(a,b)。求最小生成树。

思路：对于最小公倍数，最好的情况下就是较大的那个数本身，显然对于一个合数，我们直接接在它的最小质因子后面，他对结果的贡献就是它本身，对于一个质数，显然把他接到2后面更小。所以只需要把质数筛出来就好了，质数的贡献是2*x，合数的贡献是它本身。

1006 Xor sum https://acm.hdu.edu.cn/showproblem.php?pid=6955

大意：给定一个长度为 n 的序列a，现要求找出一段长度最小的连续的异或和，并且异或和不小于k的区间，若有多个最短的输出左端点最靠左的那个，如果不存在输出-1。 $0<=a_i<=2^{30}$ , $0<=k<=2^{30}$ ,1<=n<=100000。

思路：一看到一段连续区间的异或和最值有关的问题我们立马要想到转化成异或前缀和+字典树。首先对于异或前缀和的用法就不再描述了。求出异或前缀和之后，对于此题，我们要求的是最短的一段异或和不小于k的区间，或许我们会想，用字典树的话下标该怎么处理呢？我们要求的是最短区间，对于某个固定的右端点，显然是左端点越靠右越好。所以对于某两个数在字典树中有公共的前缀部分的话，我们只需保留下标大那个数的下标就行了。所以我们可以从左往右边查找边更新。而且我们边往右遍历，边查询右端点，此时查询的是和之前所有的前缀都存进了字典树中，因此不会有漏掉某个区间的情况。其他具体细节见代码：

#include <bits/stdc++.h>
using namespace std;
const int N=3000010;
int tr[N][2],pos[N],idx,a[N];
int n,k;
void insert(int x,int id)
{
	int  p=0;
	for(int i=29;i>=0;i--)
	{
		int u=x>>i&1;
		if(!tr[p][u])tr[p][u]=++idx;
		p=tr[p][u];
		pos[p]=id;  // 纪录下标
	}
}
int query(int x)
{
	int ans=-1;
	int p=0;
	for(int i=29;i>=0;i--)
	{
		int w=x>>i&1; // 纪录 x 这一位是0还是1
		if(!(k>>i&1)) // 如果 k 的这一位是0的话，去 1的分支一定是可以的，去0的分支也是有可能的
		{
			if(tr[p][w^1])ans=max(ans,pos[tr[p][w^1]]); // 去1的分支就没必要继续往下找了，一定是大于k了，并且该节点存的就是所有公共前缀的下表最大的那个，直接用它更新ans最大值
			p=tr[p][w]; // 继续向 0 的分支走，这个分支是有可能的
		}
		else p=tr[p][w^1]; //如果 k 这一位是 1 的话就只能往 1 的分支走
		if(!p)break;  //节点不存在直接break
	}
	if(p)ans=max(ans,pos[p]); // 如果成功走到叶子节点了，这样也是一个合法的结果，更新ans
	return ans;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	int _;
	cin>>_;
	while(_--)
	{	
		cin>>n>>k;
		for(int i=1;i<=n;i++)cin>>a[i],a[i]^=a[i-1]; // 转化成异或前缀和

		insert(0,0);//类似于前缀和，首先把0插进去 

		int ansl=0,ansr=n+1;
		for(int i=1;i<=n;i++)
		{
			int t=query(a[i])+1; // 返回的是前缀和，所以要 +1
			if(t&&i-t<ansr-ansl)ansr=i,ansl=t;
			insert(a[i],i);
		}	
		if(!ansl)cout<<-1<<"\n";
		else cout<<ansl<<" "<<ansr<<"\n";
		memset(tr,0,sizeof tr);
		idx=0;
	}
	return 0;
}

1007 pass ! https://acm.hdu.edu.cn/showproblem.php?pid=6956

大意：有 n 个人踢足球，球最开始在第一个人脚上，每一秒都要将球从当前这个人传给另一个人，设 t 秒后球在第一个脚上的方案书为 x。先给出 x , 求最小的时间 t 。 x是取模后的结果，模数 p=998244353。

思路：首先要找最小时间 t 的话，首先我们得知道对于任意一个时间 t 的方案数，也就是得先把表达式求出来。

显然有

f[0]=1,

f[1]=0,

f[2]=n-1

对于 f[3], 一秒后可能在其他n-1个人任何一个人那里，这时 3 秒变成 2秒，如果这时候要传给第一个人，那么还剩一秒必然还要传出去，不行，所以2秒的时候只能传给其他 n-2 个人。即

f[3]=(n-1) * (n-2)

对于 f[4],4秒的时候我可以传给 n-1 个人，3秒的时候我有两个分支，一是传给第一个人，这样之后的方案数也就是 f[2]. 二是传给其他 n-2 个人，对于这个分支2秒的时候只能继续传给其他n-2个人

f[4]=(n-1) * ( f[2] + (n-2) * (n-2) ) 也即是 f[4]=(n-1 * f[2] + (n-2) * f[3]

…

f[i]=(n-2) * f[i-1] + (n-1) * f[i-2]

对于形如 $f[n]=c_1 * f[n-1] + c_2 * f[n-2]$ 的递推式，我们可以用特征方程的方法求出f[n] 关于 n 的表达式，方法如下：

特征方程 $x^2= c_1 * x + c_2$

$f[n]= A * x_1^n + B * x_2^n$

所以对于 f[i]=(n-2) * f[i-1] + (n-1) * f[i-2]

特征方程为 $x^2=(n-2)x+(n-1)$

得 $x_1=n-1, x_2=-1$

所以 $f[i]=A (n-1)^i + B (-1)^i$

又因为 f[0]=1,f[1]=0;

代入得 $A=\frac{1}{n}$ $B=\frac{n-1}{n}$

所以 $f[i]=\frac{(n−1)^i+(−1)^i∗(n−1)}{n}$

显然对 i 奇偶进行讨论。

当 i 为奇数时 $f[i]=\frac{(n−1)^i−(n−1)}{n}$

即 $(n-1)^i \equiv x * n+n-1 (mod\ p)$

当 i 为偶数时

即 $(n-1)^i \equiv x * n-n+1 (mod\ p)$

形如 $a^i \equiv b (mod\ p)$ 求最小的 i 显然可以通过 bsgs 算法做。

具体实现的时候用 unordered_map T了，手写哈希快到飞起。stl 慎用

#include <bits/stdc++.h>
using namespace std;
const int M=998244353,N=114514;
typedef long long LL;
LL qmi(LL a,LL b)
{
	LL res=1;
	while(b)
	{
		if(b&1)res=res*a%M;
		a=a*a%M;
		b>>=1;
	}
	return res%M;
}
int h[N],e[N],ne[N],idx,w[N];// 哈希表——拉链法 w数组存次幂
void insert(int x,int b)
{
	int k=(x%N+N)%N;
	e[idx]=x,w[idx]=b,ne[idx]=h[k],h[k]=idx++;
}
int find(int x)
{
	int k=(x%N+N)%N;
	for(int i=h[k];i!=-1;i=ne[i])
	{
		if(e[i]==x)return w[i];// 返回次幂计算
	}
	return -1;
}
LL n,x,m,a,b;
LL bsgs()// 大步小步算法
{
	memset(h,-1,sizeof h);
	idx=0;
	LL x=b;
	insert(x,0);
	for(int i=1;i<m;i++)
	{
		x=x*a%M;
		insert(x,i);
	}
	x=1;
	int t=find(x);
	if(t!=-1)return 0;
	LL tt=qmi(a,m);
	for(int i=1;i<=m;i++)
	{
		x=x*tt%M;
		int t=find(x);
		if(t!=-1)return i*m-t;
	}
	return -1;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	m=ceil(sqrt(M));
	int _;
	cin>>_;
	while(_--)
	{
		cin>>n>>x;
		if(x==1)cout<<0<<"\n";
		else if(x==0)cout<<1<<"\n";
		else 
		{
			 LL ans=INT_MAX;
			 a=n-1;b=(x*n+n-1)%M;
			 LL t=bsgs();
			 if(t!=-1&&t%2)ans=min(ans,t);
			 //cout<<t<<"\n";
			 b=(x*n-n+1)%M;
			 t=bsgs();
			 if(t!=-1&&!(t%2))ans=min(ans,t);
			 //cout<<t<<"\n";
			 if(ans==INT_MAX)ans=-1;
			 cout<<ans<<"\n";
		}
	}
	return 0;
}

总结：要会推导式子，利用特征方将递推式变成函数式，进而用bsgs算法去求解。

1008 Maximal submatrix https://acm.hdu.edu.cn/showproblem.php?pid=6957 最大子矩阵，单调栈，悬线法

大意：给定一个 n * m 的矩阵，找到最大的每列单调不降的子矩阵，输出其面积。(1<=n,m<=2e3)

此题有两种方法：（1）单调栈（2）悬线法

（1）单调栈，先来看一到单调栈的经典题目，求宽度为1的条形图的公共部分的最大面积

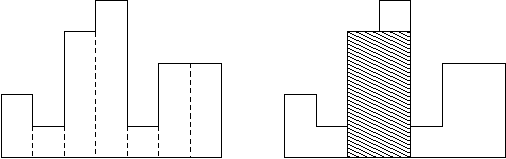
首先想想暴力怎么做，显然就这么多高度，我们可以枚举以第 i 个矩形的高度的公共矩形的高度的面积，维护面积最大值就好了。对于每个 i ，我们往左往右找到第一个高度小于它的矩形j , k 则公共部分的面积为 (k-j-1) * h[i]。

时间复杂度 O( $n^2$ ) 。怎么优化呢？对于每次找到左边第一个小于它的数？这不就是单调栈的经典操作吗？也就是维护个单调不减的栈，每次对于一个数，入栈的方式就是把栈中所有大于它的数弹出，这样就可以边弹出边更新答案，每次弹出我们的栈顶都是比当前所在位置大的，也就是我们每次计算的都是以当前栈顶往右的面积，这样我们就可以用 O(n)的时间复杂度更新最大面积了。需要注意的是边界问题，最靠右的可能是大于栈顶的，所以我们在 m+1 位置设置个负无穷确保边界位置的更新。

再来个升级版的，给定一个01矩阵，求最大全是是1的矩阵的面积。对于这题我们一行一行的求，当前行往上最多多少个连续的 1 然后这就相当于高度，然后就可以和上面的题目一样，用单调栈写了。时间复杂度 O( $n^2$ )

再来回到本题，显然我们可以把题目给出的矩阵转成01矩阵，然后就和上面的一样了。

#include <bits/stdc++.h>
using namespace std;
const int N=2010;
int g[N][N],a[N][N],n,m,w[N],stk[N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int _;
    cin>>_;
    while(_--)
    {
        cin>>n>>m;
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
            {
                cin>>g[i][j];
                if(g[i][j]>=g[i-1][j])a[i][j]=1;  // 转化成01矩阵
                else a[i][j]=0;
            }

        for(int i=1;i<=m+1;i++)w[i]=0;
        int ans=0;
        int f;
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                if(a[i][j])w[j]++;  // 转化成条形图的高度
                else w[j]=1;
            }
            f=0;
            for(int j=1;j<=m+1;j++)
            {
                while(f&&w[stk[f]]>w[j])
                {
    
                    ans=max(ans,(j-stk[f-1]-1)*w[stk[f]]);// 只要栈顶比当前位置大，就可以以当前栈顶为高更新面积，就算栈顶下面的和栈顶相等也没关系，总能更新到的
                    f--;
                }
                stk[++f]=j;
            }
        }
        cout<<ans<<"\n";
    }
    return 0;
}

（2）悬线法：悬线法的适用范围是单调栈的子集，但和单调栈相比，悬线法更加的简单，更加容易理解。

还是先来看最基础版的问题：求上图中宽度为 1 的公共部分矩形的最大面积。悬线法就是通过某个放置一条条可以左右移动的竖线，通过一定的预处理，达到 o(n) 的时间复杂度求出最大面积。对于每个高度 a[i] ，我们预处理处理，以当前 a[i] 为高度的悬线向左向右能到的最远位置，初始化显然 l[i]=r[i]=i.

分以下情况 l[i]=1 ，显然不能再往左了

$a [i] > a [l [i] - 1]$ 也不能再往左了

$a [i] < = a [l [i] - 1] ， l [i] = l [l [i] - 1]$

对于右边界 r[i] 的更新同理。对于结果最大值必定是以某个悬线为高度的面积，维护最大值就好了。

对于对问题的转化和上面的一样。

#include <bits/stdc++.h>
using namespace std;
const int N=2010;
int g[N][N],a[N][N],n,m,w[N],l[N],r[N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int _;
    cin>>_;
    while(_--)
    {
        cin>>n>>m;
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
            {
                cin>>g[i][j];
                if(g[i][j]>=g[i-1][j])a[i][j]=1;
                else a[i][j]=0;
            }

        for(int i=1;i<=m+1;i++)w[i]=0;

        int ans=0;
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                if(a[i][j])w[j]++;
                else w[j]=1;
                l[j]=r[j]=j;
            }
            for(int j=1;j<=m;j++)while(l[j]>1&&w[j]<=w[l[j]-1])l[j]=l[l[j]-1];
            for(int j=m;j>=1;j--)while(r[j]<m&&w[j]<=w[r[j]+1])r[j]=r[r[j]+1]; // 注意处理 r 的时候要从后往前更新
            for(int j=1;j<=m;j++)ans=max(ans,(r[j]-l[j]+1)*w[j]); //更新答案
        }
        cout<<ans<<"\n";
    }
    return 0;
}

总结：对于求最大子矩阵面积的题目可以考虑转化成01矩阵，然后用悬线法或者单调栈做。

1009 https://acm.hdu.edu.cn/showproblem.php?pid=6958 排序+并查集

大意：题目巴拉巴拉说了一大堆，提取出来其实也就是有 n 个点，m 条边，要分成 k 组，现在要你确定一个界限D,所有权重<=D的在同一组，所有权重>D的在不同组。求满足条件的最小的D，（对题意的理解很重要）

思路：乍一看这个题很麻烦，要找最小的 D 还得满足很多限制条件。实际上根据所有权重<=D的分到一组，以及最小的D这两个条件，我们能确定D一定是某个权重，所以我们只需要把权重从小到大排个序，然后枚举当到某个权重时分成的组数，即用并查集维护连通块的数量，最后找分成 k 组时的权重就好了。另外还有很多小细节，对于分成 n 组也是存在的，还有就是出现权重相等的时候，根据题意，我们需要在他们全部加到同一组才更新。

具体见代码：

#include <bits/stdc++.h>
using namespace std;
const int N=500010;
struct node{
    int x,y,w;
    bool operator <(const node &W)const
    {
        return w<W.w;
    }
}a[N];
int fa[100010],s[N],D[N];
int n,m,k;
int find(int x)
{
    if(fa[x]!=x)return fa[x]=find(fa[x]);
    return fa[x];
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int _;
    cin>>_;
    while(_--)
    {
        cin>>n>>m>>k;
        for(int i=1;i<=n;i++)fa[i]=i;
        for(int i=1;i<=m;i++)
        {
            int x,y,w;
            cin>>x>>y>>w;
            a[i]={x,y,w};
        }
        sort(a+1,a+m+1);
        int cnt=0;
        s[0]=n;
        int tot=n;
        for(int i=1;i<=m;i++)
        {
            int x=a[i].x,y=a[i].y;
            int fx=find(x),fy=find(y);
            if(fx!=fy)
            {
                fa[fy]=fx;
                tot--;
            }
            if(i==m||a[i].w<a[i+1].w) // 对于权重相同的边，对于某个界限时，相同权重的那些必须加到一组，要不然就不合法
            {   
                s[++cnt]=tot;
                D[cnt]=a[i].w;
            }
        }
        int f=1;
        for(int i=0;i<=cnt;i++)
        {
            if(s[i]==k)
            {
                cout<<D[i]<<"\n";
                f=0;
                break;
            }
        }
        if(f)cout<<"-1"<<'\n';
    }
    return 0;
}

总结：对题目的分析是很重要的，一般题目都不会很直白，这时候就需要我们将题目的意思做等价变化。

Eter`nal

关注

1
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
2021.杭电中超第一场.补题

1001 https://acm.hdu.edu.cn/showproblem.php?pid=6950 签到，打表找规律就好了。1005 Minimum spanning tree https://acm.hdu.edu.cn/showproblem.php?pid=6954 思维题，签到大意：现有 n 个点 (2<=n<=10000000)，任意两点a,b之间的之间的权重为 lcm(a,b)。求最小生成树。思路：对于最小公倍数，最好的情况下就是较大的那个数本身，显然对于一个.
复制链接

扫一扫