01，完全，多重，混合，分组背包相关题目

最新推荐文章于 2024-07-19 15:45:46 发布
最新推荐文章于 2024-07-19 15:45:46 发布
阅读量182 收藏
点赞数
分类专栏： 算法 文章标签： 算法 c++ 动态规划
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/m0_51641706/article/details/126669500
版权

文章目录


背包问题的状态定义基本都是：
在前i个物品选，体积不超过j的所有选法。属性可以是max， min， count

注意一点：背包问题基本都可以边读边进行dp运算。多这么写， 可以优化代码简洁度。

01背包

一维写法

#include <iostream>

using namespace std;

const int N = 1010;

int f[N][N];

int n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        int v, w;
        cin >> v >> w;
        for(int j = 0; j <= m; j++)
            if(j >= v) f[i][j] = max(f[i - 1][j], f[i - 1][j - v] + w);
            else f[i][j] = f[i - 1][j];
    }
    
    cout << f[n][m];
}

二维写法
修改方法：

  1. 把第1维删去
  2. 如果当前状态由上一层状态得出， 体积循环就要倒着循环。因为f[j]可以由f[j - v]推导而来， 而j - v是小于j的，因此如果倒着循环的话，f[j - v]存放的还是上一次循环的值，因此是可行的。如果是正着循环，f[j] = f[j - v] + w, 而f[j - v]早就被这次循环的值覆盖了，因此不可行。
#include <iostream>

using namespace std;

const int N = 1010;

int f[N];

int n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        int v, w;
        cin >> v >> w;
        for(int j = m; j >= v; j--)
            f[j] = max(f[j], f[j - v] + w);
    }
    
    cout << f[m];
}

完全背包

具体推导不写了， 很简单。把f[i][j - v]和f[i][j]的表达式比较一下即可。

很容易错的地方是：当背包放不下该物品的时候，f[i][j] = f[i - 1][j]，优化成一维后这行就变成了恒等式，因此不用写。但是f[i][j] = max(f[i-1][j], f[i][j - v] + w)只有在书包放的下的情况下才成立，因此一定要加上if！！！

二维写法：

#include <iostream>

using namespace std;

const int N = 1010;

int f[N];

int n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        int v, w;
        cin >> v >> w;
        for(int j = 0; j <= m; j++)
            if(j >= v)
                f[j] = max(f[j], f[j - v] + w);
    }
    
    cout << f[m];
}

这里要说一下一维写法，因为从一维写法才可以看出为什么完全背包可以正在循环

#include <iostream>

using namespace std;

const int N = 1010;

int f[N][N];

int n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        int v, w;
        cin >> v >> w;
        for(int j = 0; j <= m; j++)
        {
        	无论背包体积够不够，f[i][j]都必须有可能等于f[i - 1][j],因此
        	可以这么写
            f[i][j] = f[i - 1][j];
            if(j >= v) f[i][j] = max(f[i][j], f[i][j - v] + w);
			
			当然这么写也是可以的，但是这么写就看不出来为什么优化成一维后
			体积可以正着循环
			if(j >= v) f[i][j] = max(f[i - 1][j], f[i][j - v] + w)
			else f[i][j] = f[i - 1][j]
        }
    }
    
    cout << f[n][m];
}

我们可以发现，在这种写法下，f[i][j] = max(f[i][j], f[i][j - v] + w), 状态的转移并不需要上一层的状态，因此可以正着循环。

多重背包

注意要加上if判断即可。

暴力写法：

#include <iostream>

using namespace std;

const int N = 110;

int n, m;

int f[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        int v, w, s;
        cin >> v >> w >> s;
        for(int j = m; j >= 0; j--)
            for(int k = 0; k <= s; k++)
                if(k * v <= j)
                    f[j] = max(f[j], f[j - k * v] + k * w);
    }
    
    cout << f[m];
}

二进制优化写法：
原理：二进制 + 一个常数可以表示任意实数。比如10可以用1 2 4三个二进制 + 一个3来表示。又比如20可以用1 2 4 8 +一个5来表示。

因此多重背包，每一个物品的个数可以被拆成若干个01背包。比如该物品有20个，可以拆成{v, w}, {2v, 2w}, {4v, 4w}, {8v, 8w}, {5v, 5w}五个01背包。

因此把任意实数R写成1 + 2 + 4 + … + 2^(n - 1) + c
条件是：2^(n) - 1 < R

代码:

#include <iostream>

using namespace std;

const int N = 1010;

int f[N];


int n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        int v, w, s;
        cin >> v >> w >> s;
        for(int k = 1; k <= s; k *= 2)
        {
        	k是当前01组的个数， 每次分配完一组，都可以开始计算dp了
        	每次分配完一组，都要将这组对应的个数减去，因此要s -= k
        	直到减到剩下物品没有办法凑成2的n次方了，证明到了最后一个数了
            for(int j = m; j >= k * v; j--)
                f[j] = max(f[j], f[j - k * v] + k * w);
            s -= k;
        }
        
        如果最后一个数不为0，证明任意常数c不为0，分为最后一组
        if(s)
        {
            for(int j = m; j >= s * v; j--)
                f[j] = max(f[j], f[j - s * v] + s * w);
        }
    }
    
    cout << f[m];
}

混合背包

混合背包指的是每一个物品个数可能只有1个，可能有无限个，可能有限个。
做法就是三种背包问题结合起来即可。

当然也可以把完全背包，01背包转换成多重背包。完全背包的物品个数等于总体积 / 单个物品的体积， 01背包的物品个数就是1.

代码：

#include <iostream>

using namespace std;

const int N = 1010;

int f[N];

int n, m;

int main()
{
    cin >> n >> m;
    for(int i = 0; i < n; i++)
    {
        int v, w, s;
        cin >> v >> w >> s;
        if(s == 0)
            for(int j = v; j <= m; j++)
                f[j] = max(f[j], f[j - v] + w);
        else
        {
            if(s == -1) s = 1;
            for(int k = 1; k <= s; k *= 2)
            {
                for(int j = m; j >= k * v; j--)
                    f[j] = max(f[j], f[j - k * v] + k * w);
                s -= k;
            }
            
            if(s)
            {
                for(int j = m; j >= s * v; j--)
                    f[j] = max(f[j], f[j - s * v] + s * w);
            }
        }
    }
    
    cout << f[m];
}

分组背包

分组背包就不要一边读一边计算dp了。先把组分好了再计算会比较清晰。

#include <iostream>

using namespace std;

const int N = 110;

int n, m;
int f[N];
int v[N][N], w[N][N], s[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        int ss;
        cin >> ss;
        for(int j = 1; j <= ss; j++)
        {
            int vv, ww;
            cin >> vv >> ww;
            v[i][j] = vv, w[i][j] = ww;
        }
        s[i] = ss;
    }
    
    
    
    for(int i = 1; i <= n; i++)
        for(int j = m; j >= 0; j--)
            for(int k = 0; k <= s[i]; k++)
                if(v[i][k] <= j) 
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
                    
    cout << f[m];
}

采药

采药
这是一道裸01背包问题。
ac代码：

#include <iostream>

using namespace std;

const int N = 1010;

int f[N];

int n, m;

int main()
{
    cin >> m >> n;
    for(int i = 1; i <= n; i++)
    {
        int v, w;
        cin >> v >> w;
        for(int j = m; j >= v; j--)
            f[j] = max(f[j], f[j - v] + w);
    }
    
    cout << f[m];
}

装箱问题

装箱问题
考点：01背包。题中要求剩余体积最小，也就是装入物品体积最大。我们可以把价值等同于体积来求01背包。

ac代码：

#include <iostream>

using namespace std;

int n, m;

const int N = 50;

int v[N], w[N], f[20010];

int main()
{
    cin >> m >> n;
    for(int i = 1; i <= n; i++) cin >> v[i], w[i] = v[i];
    
    for(int i = 1; i <= n; i++)
        for(int j = m; j >= v[i]; j--)
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        
    cout << m - f[m];
}

宠物小精灵之收服

宠物小精灵之收服

考点：二维费用的01背包。这道题如果没有深刻理解01背包的状态定义就很容易错。
1.01背包的状态定义是在前i个物品里面， 背包体积不超过j的所有选法集合。这里要明确，背包体积不超过j有花费背包体积不超过j的意思。

2.花费的概念很重要， 因为这题最后要你求在价值最大的情况下，皮卡丘的剩余体力最大。剩余体力最大也就是花费体力最小，也就是j最小的情况。

3.还有一点：皮卡丘的体力不可以为0， 我之前犯过的错误就是写成了0 < j <= m， 然而这是不正确的。j代表的是花费的体积而不是剩余的体积。因此正确答案应该是0 <= j < m， j不能等于m。一旦等于m代表皮卡丘花费的体力为m，那么剩余体力就是0了。不符合题意。

#include <iostream>

using namespace std;

int n, m, k;

const int N = 1010, M = 510, K = 110;

int f[N][M];

int main()
{
    cin >> m >> k >> n;
    for(int i = 1; i <= n; i++)
    {
        int v1, v2;
        cin >> v1 >> v2;
        for(int u = m; u >= v1; u--)
            for(int j = k - 1; j >= v2; j--)
                f[u][j] = max(f[u][j], f[u - v1][j - v2] + 1);
    }
    
    cout << f[m][k - 1] << ' ';
    
    int res = 0;
   for(int i = 0; i <= k - 1; i++)
        if(f[m][i] == f[m][k - 1])
        {
            res = i;
            break;
        }
    cout << k - res;
}

数字组合

数字组合
考点：01背包求方案个数。也就是属性是count的情况
转移方程是:如果放得下的话：f[j] = f[j] + f[j - v]
初始化f[0] = 1， 因为要组合的数字是0的话，不需要任何数字都是一个方案。

ps：这种是恰好情况的01背包，之前做的大多数都是背包体积不超过j的01背包。之后还有背包体积不小于j的01背包。它们三个的状态转移方程是完全一样的，但是循环范围和初始化方式不同。且恰好情况一般求count，不超过情况一般求max，不小于情况一般求min

#include <iostream>

using namespace std;

const int M = 10010;

int f[M];

int n, m;

int main()
{
    cin >> n >> m;
    f[0] = 1;
    for(int i = 1; i <= n; i++)
    {
        int v;
        cin >> v;
        for(int j = m; j >= v; j--)
            f[j] = f[j] + f[j - v];
    }
    cout << f[m];
}

买书

买书
考点：完全背包求方案数量。本质还是count属性
在放的下的情况下:f[j] = f[j] + f[j - v]

#include <iostream>

using namespace std;

int v[5] = {0, 10, 20, 50, 100};

int n;

const int N = 1010;
int f[N];

int main()
{
    cin >> n;
    
    f[0] = 1;
    for(int i = 1; i <= 4; i++)
        for(int j = v[i]; j <= n; j++)
            f[j] = f[j] + f[j - v[i]];
            
    cout << f[n];
}

货币系统

和买书是一模一样的题目。

#include <iostream>

using namespace std;

const int N = 3010;

long long f[N];

int n, m;

int main()
{
    cin >> n >> m;
    f[0] = 1;
    for(int i = 1; i <= n; i++)
    {
        int v;
        cin >> v;
        for(int j = v; j <= m; j++)
            f[j] += f[j - v];
    }
    
    cout << f[m];
}

庆功会

考点：二进制优化多重背包裸题。

#include <iostream>

using namespace std;
const int N = 6010;

int n, m;
int f[N];
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        int v, w, s;
        cin >> v >> w >> s;
        for(int k = 1; k <= s; k *= 2)
        {
            for(int j = m; j >= k * v; j--)
                f[j] = max(f[j], f[j - k * v] + k * w);
            s -= k;
        }
        
        if(s)
        {
            for(int j = m; j >= s * v; j--)
                f[j] = max(f[j], f[j - s * v] + s * w);
        }
    }
    
    cout << f[m];
}

二维费用背包问题

和宠物小精灵那道题目差不多，考点都是二位费用的01背包问题。直接一维是体积，一维是重量即可。

#include <iostream>

using namespace std;

const int N = 110;

int f[N][N];

int n, m, k;

int main()
{
    cin >> n >> m >> k;
    for(int i = 1; i <= n; i++)
    {
        int v, w, ww;
        cin >> v >> w >> ww;
        for(int j = m; j >= v; j--)
            for(int u = k; u >= w; u--)
                f[j][u] = max(f[j][u], f[j - v][u - w] + ww);
    }
    
    cout << f[m][k];
}

潜水员

考点：求最小值的二维背包问题。
之前说过，不管是最小，最大，还是恰好，它们的转移方程都是一样的。但是循环范围和初始化不同。

有题意得状态定义是氧气体积不少于j， 氮气体积不少于k的所有选法。属性是min。
对于求min的背包问题，所有格子都要初始化成INF（不然求不了min）。f[0][0] = 0，因为氧气氮气体积不少于0，那么最小重量一定是0.

关于循环范围的问题。由于状态定义是体积不少于某个数，那么这个数若是负数的话，状态定义也是成立的。（不少于一个负数题目中所有情况都符合，但是负数索引会越界，因此不少于负数可以全部当成不少于0的状态，也就是最小重量为0）

在这里插入图片描述

循环范围： 求体积不超过j的时候，一定要注意放不下的情况，因此一般都是 j = m; j >= v; j–等等
求体积至少为j的时候，一定要注意负数是可行的，因此一般都是j = m; j >= 0; j–

#include <iostream>
#include <cstring>
using namespace std;

const int N = 100;

int n, m, k;
int f[N][N];

int main()
{
    cin >> n >> m >> k;
    
    memset(f, 0x3f, sizeof f);
    f[0][0] = 0;
    for(int u = 1; u <= k; u++)
    {
        int v1, v2, w;
        cin >> v1 >> v2 >> w;
        for(int i = n; i >= 0; i--)
            for(int j = m; j >= 0; j--)
                f[i][j] = min(f[max(0, i - v1)][max(0, j - v2)] + w, f[i][j]);
    }
    
    cout << f[n][m];
}

机器分配

机器分配
考点：分组背包+输出具体选择的方案

分组背包不再赘述，讲一讲怎么输出背包问题的具体方案。

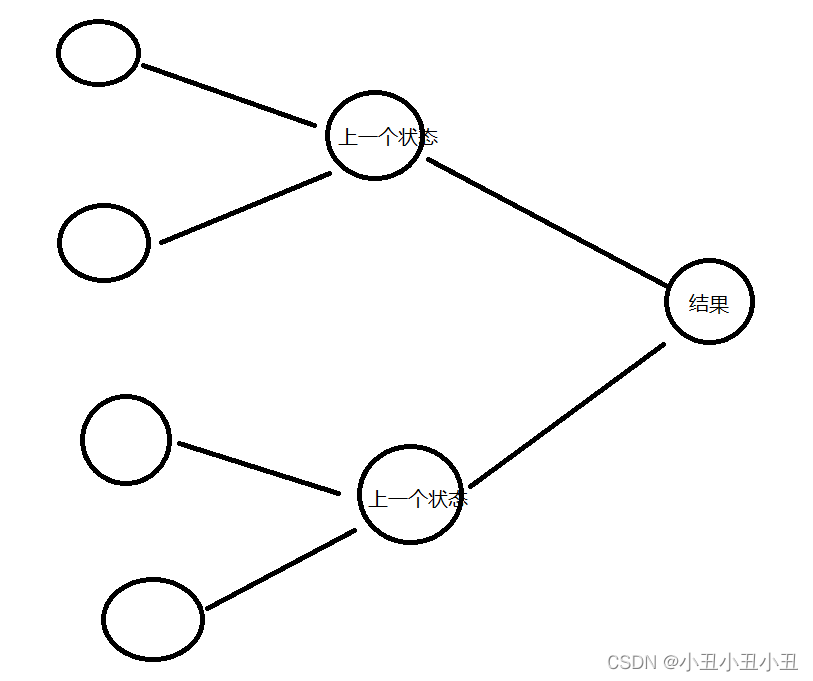
关键操作在于倒推。加入f[i][j] = f[i-1][j-v] + w,则证明我选了当前的物品。若f[i][j] = f[i -
1][j]则证明没有选当前物品。
ps：求背包具体方案不能优化空间，因为要保存所有状态信息。优化了只有一层的状态了。无法倒推。

还要注意一点，m>=v[i][k]才可以继续倒推，背包体积一定要放得下这个物品才行。

在这里插入图片描述

#include <iostream>
#include <iostream>

using namespace std;

const int N = 20;

int f[N][N];
int v[N][N], w[N][N], s[N];

int n, m;

int main()
{
    cin >> n >> m;
    
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            int ww;
            cin >> ww;
            v[i][j] = j, w[i][j] = ww;
        }
    }
    
    for(int i = 1; i <= n; i++)
        for(int j = 0; j <= m; j++)
            for(int k = 0; k <= m; k++)
                if(v[i][k] <= j)
                    f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
    
    cout << f[n][m] << endl;
    
    for(int i = n; i >= 1; i--)
        for(int k = 0; k <= m; k++)
        {
            if(m >= v[i][k] && f[i][m] == f[i - 1][m - v[i][k]] + w[i][k])
            {
                cout << i << ' ' << k << endl;
                m -= v[i][k];
                break;
            }
        }
    
    
}

求背包问题的具体方案（输出字符串字典序最小）

求背包问题的具体方案
考点：求背包问题的具体方案，方法还是倒推。

由于这次要求字典序最小，因此要从第一件物品开始输出，然而我们是要倒推的。因此我们要让f[1][1]是最终的结果状态。f[n][m]是最初的状态。

因此倒着循环计算dp即可。

易错点：该物品要放得下才可以继续倒推！！！背包问题里面不要老是忘记加这个条件！！！

#include <iostream>
using namespace std;

const int N = 1010;

int f[N][N], V[N], W[N];

int n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        int v, w;
        cin >> v >> w;
        V[i] = v, W[i] = w;
    }
    
    
    for(int i = n; i >= 1; i--)
    {
        for(int j = m; j >= 0; j--)
        {
            f[i][j] = f[i + 1][j];
            if(j >= V[i]) f[i][j] = max(f[i][j], f[i + 1][j - V[i]] + W[i]);
        }
    }
    int j = m;
    for(int i = 1; i <= n; i++)
    {
        if(j >= V[i] && f[i][j] == f[i + 1][j - V[i]] + W[i])
        {
            cout << i << ' ';
            j -= V[i];
        }
    }
}

物品是不同策略的背包问题

金明的预算方案
考点：用二进制枚举所有情况转换成分组背包的问题。

这题说的是：要买附件就必须先买主件。因此可以将买主件和附件排列组合一下。
比如：如果有两个附件一个主件，可以组合成四种情况
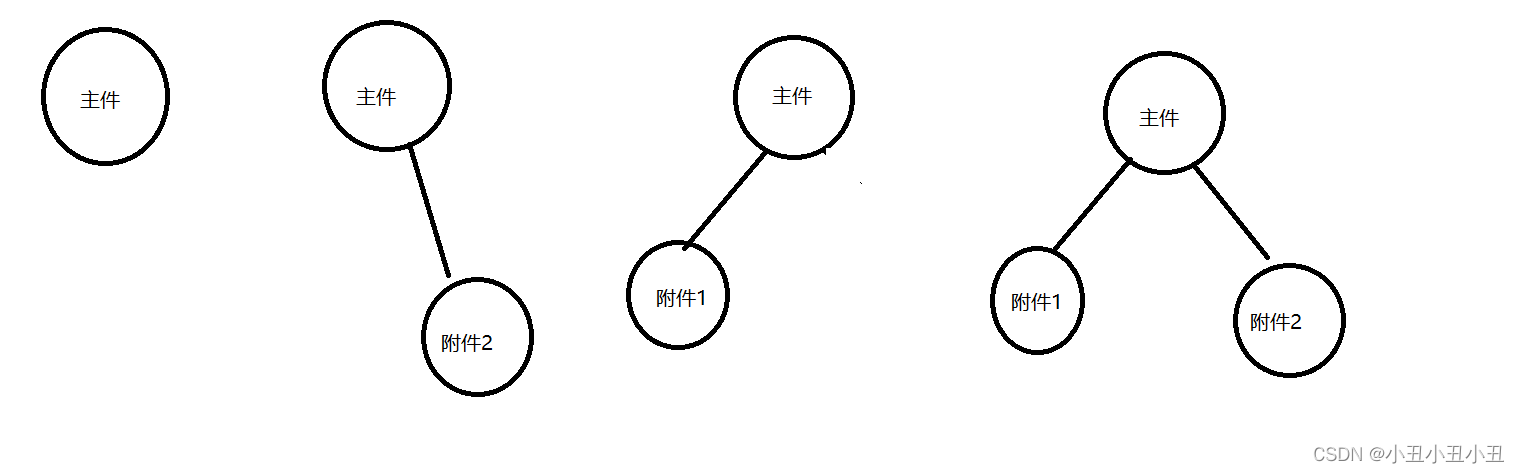
在这里插入图片描述
这四种情况可以是一组背包，每一个决策只能选一次，因为只有一个主件。这样就转换成分组背包问题了。

我们发现，策略的个数是2^(附件数量).因为每一个附件都有选和不选两种情况。

所以可以用二进制枚举所有情况：下面给出代码模板：

for(int k = 0; k < 1 << xx.size(); k++)所有情况.比如2^2 = 4
{
    for(int u = 0; u < xx.size(); u++)每种情况的选择对象，这里是2
    {
        if(1 << u & k)如果这一位是0代表不选，是1代表选
        {
            xxxxxxxx
        }
    }
   	xxxxxxx
}

ac代码：

#include <iostream>
#include <vector>
using namespace std;

const int N = 32010, M = 100;

typedef pair<int, int> pii;

pii master[M];
vector<pii>servent[M];
vector<pii> group[M];
int f[N];

int n, m;

int main()
{
    cin >> m >> n;
    for(int i = 1; i <= n; i++)
    {
        int v, w, s;
        cin >> v >> w >> s;
        if(!s)
            master[i] = {v, v * w};
        else
            servent[s].push_back({v, v * w});
    }
    
    int cnt = 0;
    for(int i = 1; i <= n; i++)
    {
        if(master[i].first)
        {
            cnt++;
            for(int k = 0; k < 1 << servent[i].size(); k++)
            {
                int tmp_v = master[i].first, tmp_w = master[i].second;
                for(int u = 0; u < servent[i].size(); u++)
                {
                    if(1 << u & k)
                    {
                        tmp_v += servent[i][u].first;
                        tmp_w += servent[i][u].second;
                    }
                }
                group[cnt].push_back({tmp_v, tmp_w});
            }
        }
    }
    
    for(int i = 1; i <= cnt; i++)
        for(int j = m; j >= 0; j--)
            for(int k = 0; k < group[i].size(); k++)
                if(group[i][k].first <= j)
                    f[j] = max(f[j], f[j - group[i][k].first] + group[i][k].second);
    cout << f[m];
}
小丑小丑小丑
关注
  • 0
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
背包问题（01背包、完全背包、多重背包、混合背包、分组背包）
weixin_62355410的博客
03-11 1192
题目描述 小明有一个容量为V 的背包。 这天他去商场购物，商场一共有N件物品，第i件物品的体积为 wi​，价值为 vi​。 小明想知道在购买的物品总体积不超过 V的情况下所能获得的最大价值为多少，请你帮他算算。 输入描述 输入第1行包含两个正整数N,V表示商场物品的数量和小明的背包容量。 第2∼N+1行包含2个正整数w,v表示物品的体积和价值。 1≤N≤10^2， 1≤V≤10^3，1≤wi​,vi​≤10^3。 输出描述 输出一行整数表示小明所能获得的最大价值。 ...
背包之01背包、完全背包、多重背包详解.
07-31
本文将详细解析三种常见的背包问题：01背包、完全背包和多重背包。 首先，我们来了解01背包问题。01背包问题的名字来源于每个物品只能选择放入背包（1）或不放入（0）。问题定义如下：给定n个物品，每个物品有自己...
01，完全，多重背包，背包问题（Python）
ZHE
04-27 7135
文章目录概述01-背包问题题目描述：分析原分析扩展分析代码完全背包题目描述分析代码原分析代码二维dp转一维dp代码省略取物品次数k的等价转换代码多重背包 概述 01-背包问题 完全背包问题 多重背包问题 多重背包暴力解法。 多重背包二进制优化方法解法。 多重背包单调队列优化解法。 混合背包问题 二维费用背包问题 分组背包问题 背包问题求方案数 求背包问题的方案 有依赖的背包问题 01-背...
背包DP问题（01背包+完全背包+分组背包+多重背包+混合背包+二维费用的背包）
柠檬的博客~~~
08-17 1298
背包DP问题 01背包问题 一、01背包问题 问题： 有N件物品和一个容量为V的背包。第i件物品的费用（即体积，下同）是w[i]，价值是c[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。 基本思路： 　　这是最基础的背包问题，特点是：每种物品仅有一件，可以选择放或不放。 　　用子问题定义状态：即f[i][v]表示前i件物品(部分或全部)恰放入一个容量为v的背包...
ch4(DP)——背包问题（01背包、完全背包、多重背包、分组背包、混合背包）
kingdom365的博客
09-01 299
1.自然语言描述 ① 01背包问题：有n个物品，每个物品有相应的体积vi和价值wi，对于一个物品，要么装入背包，要么不装入；有一个体积为V的背包，怎么装物品才能使背包中物品的价值最大？ ② 完全背包问题：有n种物品，每种物品有相应的体积vi和价值wi，对于一种物品可以选任意多个装入背包（即每种物品的数量是无穷大的）有一个体积为V的背包，怎么装物品才能使背包中物品的价值最大？ ③ 多重背包问题：有n种物品，每种物品有相应的体积vi和价值wi，第i种物品的数量是si个；有一个体积为V的背包，怎么装物品才能使背包
背包之01背包、完全背包、多重背包详解1
08-04
本文主要探讨了01背包、完全背包和多重背包三种类型的背包问题，并结合动态规划的四个基本步骤进行了解析。 01背包是最基础的背包问题，每种物品仅有一件，可以选择放或不放。状态定义为`f[i][v]`，表示前`i`件物品...
背包问题详解（01背包，完全背包，多重背包，混合背包，二维费用背包……）
10-16
4. **混合背包问题**：结合了01、完全和多重背包的特点，需要灵活处理不同类型的物品限制。 5. **二维费用的背包问题**：除了考虑重量限制外，还增加了费用限制，使得问题变得更复杂，需要同时考虑价值和费用的权衡...
线性、区间、树形、01背包、多重背包等动态规划算法一次学会
04-05
在这个"线性、区间、树形、01背包、多重背包等动态规划算法一次学会"的资源中，我们可以学习到动态规划的多种应用形式。 1. **线性动态规划**：线性动态规划通常涉及一维数组，问题往往与序列或序列操作有关。例如...
01规划背包问题讲解PPT+源码+word
03-29
在以下六篇讲解中，我们将深入探讨背包问题的各种变体，包括0/1背包、完全背包、多重背包等，以及如何使用动态规划来解决它们。我们会详细解释动态规划的思路、状态转移方程的设计、以及如何处理边界条件。 同时，...
【18】输出字符菱形
2301_78786609的博客
07-19 359
用‘*’构造一个对角线长n个字符，倾斜放置的菱形。
(C++二叉树02) 翻转二叉树 对称二叉树 二叉树的深度
qq_44962949的博客
07-17 244
【代码】(C++二叉树02) 翻转二叉树 对称二叉树 二叉树的深度。
Leetcode—207. 课程表【中等】
最新发布
Atticus的博客
07-19 293
运行结果 之后我会持续更新，如果喜欢我的文章，请记得一键三连哦，点赞关注收藏，你的每一个赞每一份关注每一次收藏都将是我前进路上的无限动力 ！！！↖(▔▽▔)↗感谢支持！
算法刷题笔记 排列数字（C++实现）
hanmo22357的博客
07-17 302
一道简单的深度优先搜索（DFS）模板题，给出了DFS问题的一般思路以及C++代码实现
24暑假算法刷题 | Day15 | LeetCode 110. 平衡二叉树，257. 二叉树的所有路径，404. 左叶子之和，222. 完全二叉树的节点个数
weixin_54468359的博客
07-17 1169
day15打卡：二叉树的递归与迭代
(算法)区间调度问题
2202_75519246的博客
07-17 236
此外,参与工作的时间段不能重复(即使是开始的瞬间和结束的瞬间的重叠也是不允许的). 你的目标是参与尽王多的工作,那么最多能参与多少项工作呢?有n项工作,每项工作分别在s时间开始,在t时间结束. 对于每项工作,你都可以选择参与与否,如果选择了参与,那么自始至终都必须全程参与.
游戏中的敏感词算法初探
555.add(111)
07-17 446
在游戏中起名和聊天需要服务器判断是否含有敏感词，从而拒绝或屏蔽敏感词显示，这里枚举一些常用的算法和实际效果。
《算法笔记》总结No.8——双指针
前端，算法，MATLAB，统计学爱好者，目前主攻Web全栈+考研内容
07-17 1065
去年发表过较简单的双指针案例，建议先行阅读~C++实现双指针算法_c++ 双指针排序-CSDN博客文章浏览阅读154次。本贴介绍双指针的入门典例~_c++ 双指针排序https://jslhyh32.blog.csdn.net/article/details/129829790相比说双指针是一种算法，他更倾向是一种编程技巧，话不多说直接看一个引例：如下，给定递增序列【1,3,5,7,9】，寻找到两个相加为16的元素。如果使用暴力的思想，相当于是一个双层循环：外层下标i对应的A[i]和内层下标为j的A[j]之
前缀和算法——部分OJ题详解
aaqq800520的博客
07-17 997
（文章的题目解释可能存在一些问题，欢迎各位小伙伴私信或评论指点（双手合十））
分组背包算法详解：解决ACM竞赛中的优化决策
分组背包问题可以归类为背包问题的不同变种之一，包括01背包、完全背包、多重背包、混合背包、二维费用背包等。其中，01背包是最基础的版本，而分组背包则增加了物品间的冲突性，需要更加细致地考虑物品选择策略。 ...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值