数据结构与算法——11.递归

最新推荐文章于 2024-04-17 15:58:40 发布

L纸鸢

最新推荐文章于 2024-04-17 15:58:40 发布

阅读量693

点赞数 1

分类专栏：数据结构与算法文章标签：算法 java

本文链接：https://blog.csdn.net/m0_52096593/article/details/132163308

版权

数据结构与算法专栏收录该内容

37 篇文章 3 订阅

订阅专栏

这篇文章我们来讲一个很常用的算法思想——递归

1.递归的概述

递归的定义：在计算机科学中，递归是一种解决计算问题的方法，其中解决方案取决于同一类问题的更小子集。

下面用单链表的递归遍历来说明解释一下：

void f(Node node){
    if(node == null)
        return;
    System.out.print(node.value);
    f(node.next);
}

解释：

上述代码的特点是在函数内部自己调用了自己，如果我们把每个函数看成是某一种问题的解决方法，自己调用自己说明下次的这个调用还是解决这个问题，说明函数解决的是同一类问题。如果这个函数中调用了别的函数，那么就说明你解决的不是同一类问题了，这就不是递归了（其实还是有的绕，不是很清楚）
每次调用，函数处理的数据会较上次缩减（子集），而且最后会缩减至无需递归（函数自己内部调用时，一定是当前函数处理集合的一个子集）
内层函数调用（子集处理）完成，外层函数才能算调用完成

自我解释：

首先看一下定义：取决于同一类问题的更小子集。分开看，同一类问题，表示要自我调用。更小子集，说明递归最终的本质是这类问题的最小子集的解决方案，也可以理解成只有我们解决了这类问题的最小子集，我们才能解决这类问题。

对于递归，我们首先还是要分解问题，分解之后会发现子问题的解决与原问题的解决方法相同，然后再分解，发现还是相同，这时就要想到递归，要想到如何去构造递归，要清楚当前问题的最小子集是什么，最小子集应该怎么解，然后再去构造递归

我们在java基础中学过循环，那里的循环是对变量的循环，而递归就是对方法的循环。循环的控制变量，对应递归方法的出入参；循环条件的选定，对应循环子集的最终界定即递归节点的判断；循环变量的累加，对应递归子集的划分。所以，递归是对方法的循环。

下面对链表遍历中的递归进行分析：

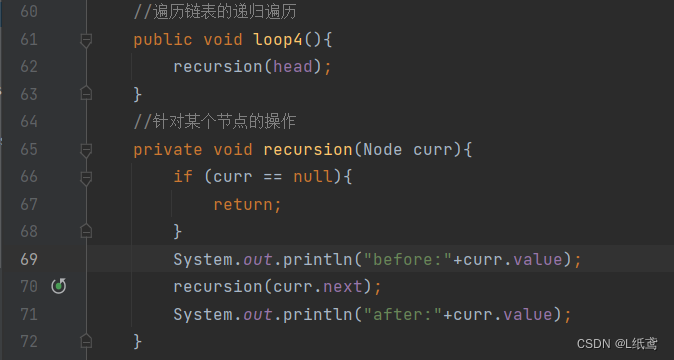
主要的递归方法是recursion，先不看方法，先想一想链表是怎么遍历的。首先是找到链表的一个头节点，然后打印输出它的值，然后让它指向它的下一个节点，然后再打印输出，然后再指向下一个，然后再打印输出……这就是链表遍历的全过程。这是很容易看出来，这个问题的最小子集是找到一个节点，打印输出它的值，然后让它指向它的下一个节点。这就我们的方法主体。然后要做的就是用递归循环这个方法。什么时候结束？当节点为null的时候结束。现在条件有了，来写方法。有返回值吗？没有；要接收参数吗？要接收节点；方法的内容是啥？打印输出。怎么递归？让当前节点指向它的下一个节点；什么时候结束？节点为null的时候结束。综上，方法就写出来了，然后再改吧改吧，调试调试就OK了。这就是最基础递归思考的方法。

这个是很简单的递归问题，下面看一个稍微复杂点的——快速排序。

快排的核心思想是：找一个基准点，然后想方法进行比较，最终让比基准点小的数在基准点的左边，比基准点大的数在基准的右边，然后再递归。

这个其实也很简单，这个问题的最小子集就是找基准点，比较，交换元素。我们只需要循环这个方法就可以了。什么时候递归结束呢？当只有一个元素的时候，递归就结束了。这样，快排的递归思想，我们就想完了，至于方法里面具体怎么写，这里就不过多讨论了。

递归的思路：

1.确定问题能否使用递归求解

2.推导出递归关系，即父问题和子问题的关系，以及递归的结束条件

例如之前遍历链表的递推关系为：

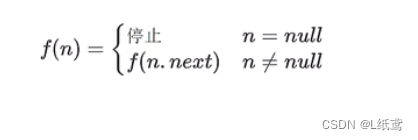
深入到最里层叫做递；从最里层出来叫做归；在递的过程中，外层函数内的局部变量（以及方法参数）并未消失，归的时候还可以用到

2.用递归求阶乘

下面看一下问题描述：
阶乘的定义 n! = 1·2·3……(n-2)·(n-1)·n，其中n为自然数，当然0！=1

递推关系：

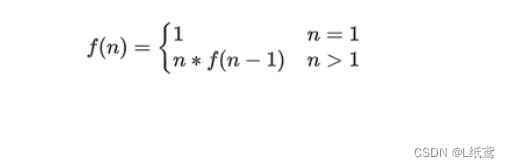
代码如下：

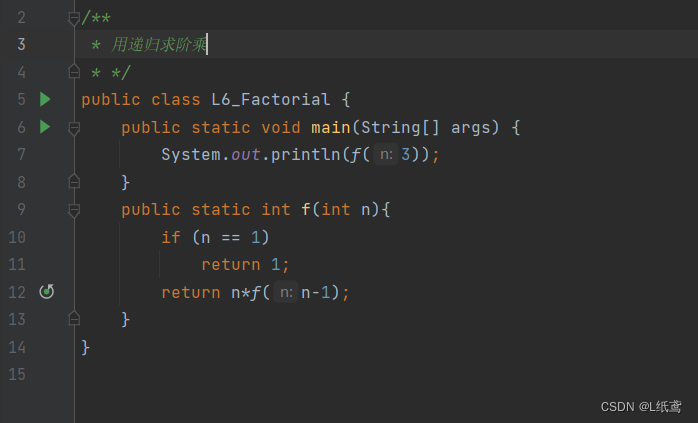
简要分析一下：比如我们要求3的阶乘，那么我们就要求2的阶乘，要求2的阶乘，就要求1的阶乘，当值等于1的时候，再往会返回，这样2的阶乘就出来了，然后3的阶乘就出来了。这段话的意思是说，对于递归，我们问题的求解取决于其子问题的求解。

3.用递归反向打印字符串

题目描述：

用递归反向打印字符串，n为字符在整个字符串str中的索引位置

递推关系：

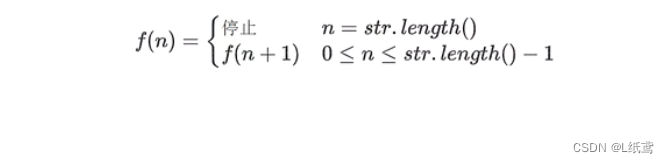
代码实现：

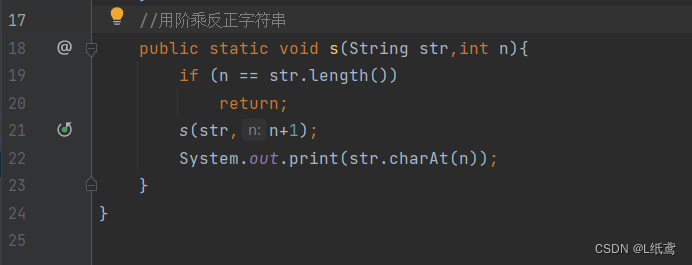
解析：

我一开始写的时候，遗忘了charAt这个方法，并且不清楚字符串居然还有索引，所以就想先转字符数组，然后倒序数组，然后再合成字符串来打印，但是这样做用不了递归，所以就放弃了。后来看了解答，它的核心还是先找到最后一个字符，打印，然后再往前归，一直到变量等于数组长度时为止，这里其实有点绕，与递归的具体执行逻辑有关。

4.用递归来求解二分查找

二分查找的核心思路：给定一个有序数组，定义两个游标，求两个游标的中间索引处的值，如果比目标值大，则在中间索引的左边查找，如果小，则在右边找。

代码实现：

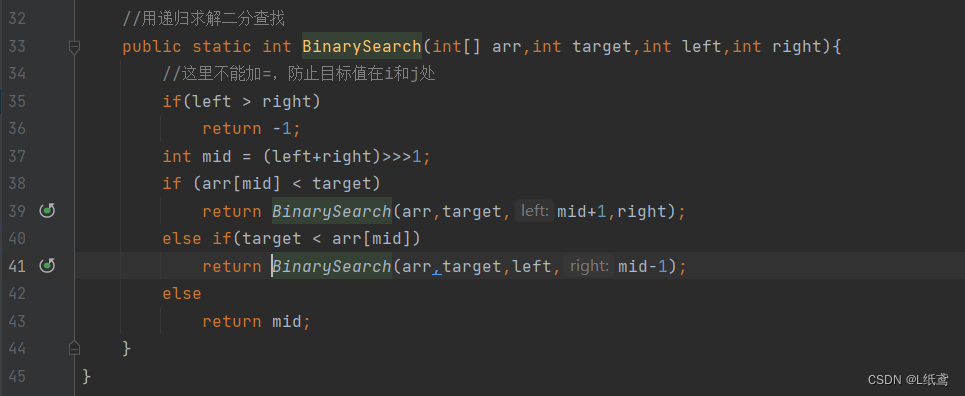这个其实是比较简单的。其中的关键就是你要明白你要干什么，要得到什么，你要从最底层得到什么，这个一定要清晰。就比如这个方法，我要从最底层得到目标值的索引，找到了，返回索引，没找到，返回-1.

我们再来看一下二分查找的非递归版本：

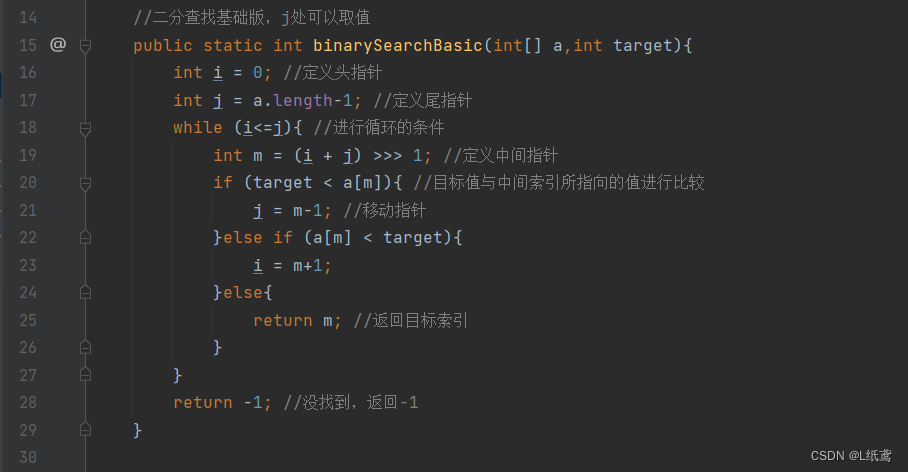
可以看出，我们的递归版大致就是将while内部的方法进行了一种抽取。

5.用递归解决冒泡排序

冒泡排序的核心思想：给定一个无序的数组，然后让相邻的两个元素进行排序，如果左边元素大于右边的元素，则交换这两个元素的位置，这样一轮下来，最大的元素就在最右边了

代码实现：

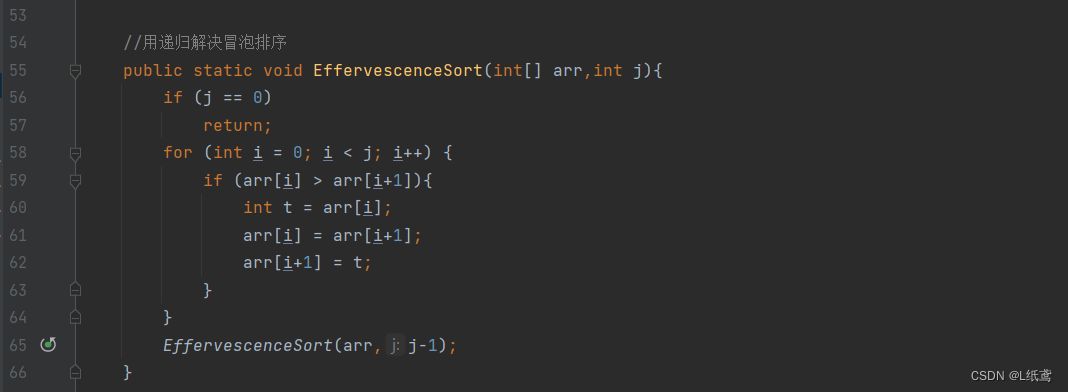
分析：这个没啥好分析的，就是每次递归排一个元素，然后就少一个元素。

问题：有这样一种情况，第一次递归，我们排好了最后的一个的元素，此时数组里面就第一个和第二个元素的位置是错的，这时我们进行第二次递归，前两个元素排好的同时，倒数第二个元素也排好了，此时，按照原来的程序看，我们还要继续许多轮递归，直到只剩一个元素为止。但实际上后面的这么多轮递归都没干到啥事，就在空耗资源，这个问题怎么解决？

答：设置一个变量x，当发生 i 与 j 发生交换时，就让x等于 i 处的索引，然后再从0到x处进行递归。如果x的没变，说明 i 与 j 没有发生交换，就说明数组是有序的，这样就不用递归了，就解决了上面的问题。

代码实现：

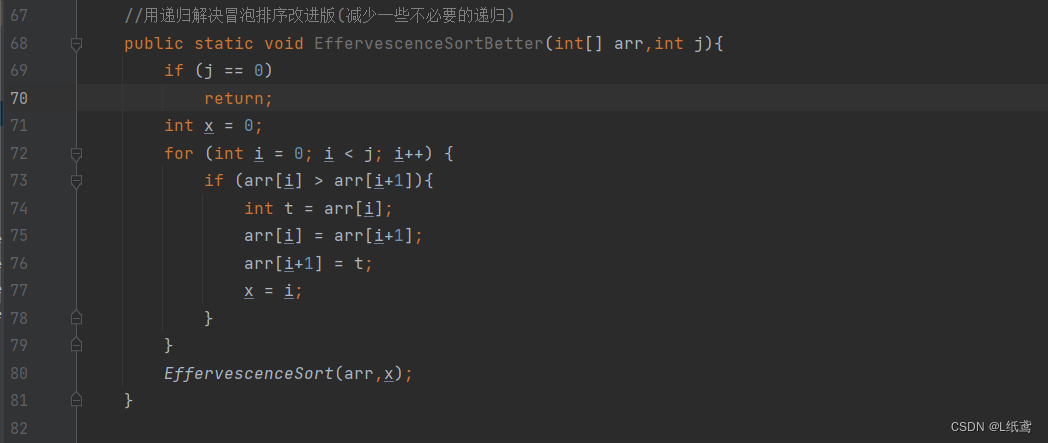
拓展：一开始看到这个问题的时候，我想到的是递归一次后，对前面的数进行一下检查，就是看前面的数是不是有序的，如果是，就退出，不是就继续递归，想到了sort方法。但仔细一想，这肯定不现实，于是放弃。后来看了解答，就是只用了一个变量就解决了，就突然有种很奇妙的感觉。于是感觉，这应该就是算法吧。告诉了你方法，那代码就肯定会写。但关键是这个方法是什么？或者说，方法有许多，代码也有许多，如何用自己会的代码去实现那些方法？我觉得这应该是重点。

6.用递归解决插入排序

插入排序的核心思想：

给定一个无序的数组，将其分为两部分，一部分是左边排好序，一部分是右边无序的，然后将无序里面的元素依次和有序部分的进行比较，直到找到合适的位置，然后插入该元素。

代码实现：

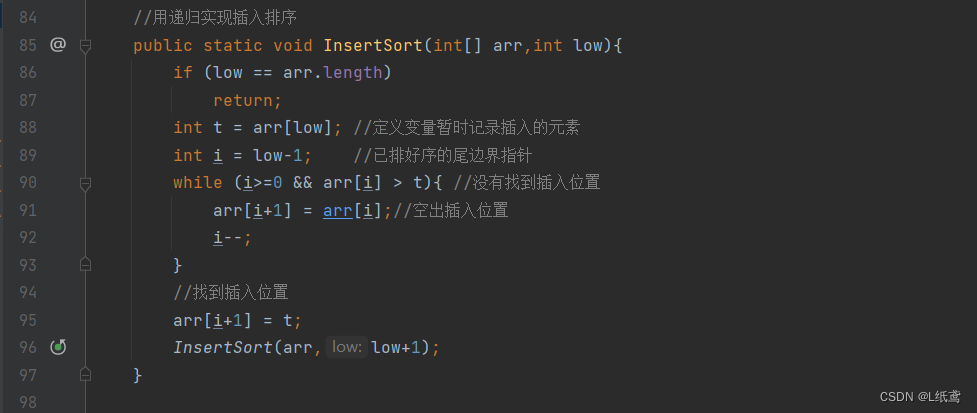
解析：这里的递归很容易理解，和上面的冒泡排序差不多。难点在于如何交换。我一开始想到的是数组的copy方法，但是感觉很复杂，看了答案后，用一个变量暂存值就能解决了，很简单。这就是算法的思想。

问题：如果我们要插入的元素刚好在正确的位置，那代码是不是可以优化？

答：是，优化后的代码如下：

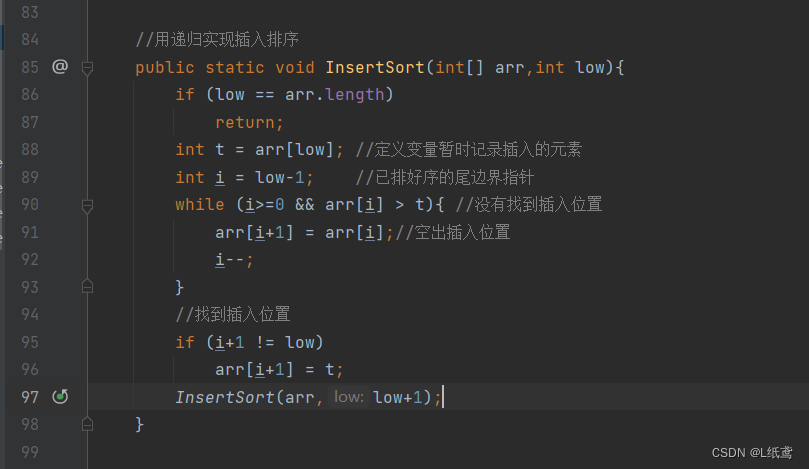
下面看一下插入排序的另外一种实现方法：

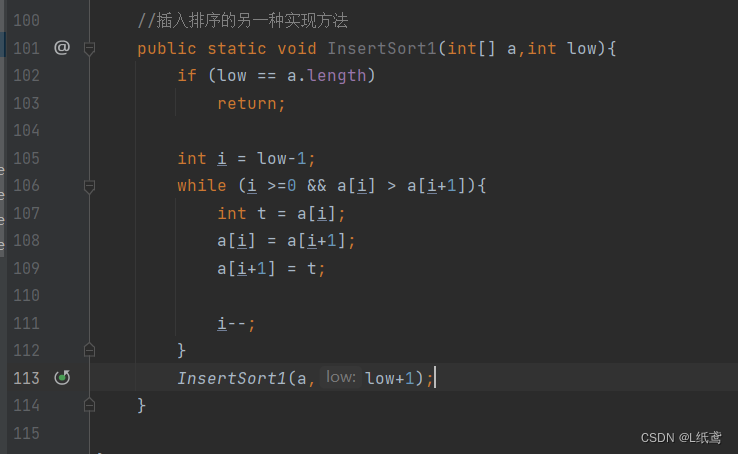
和冒泡排序很相似，可以说是逆序的冒泡排序。

7.用递归解决斐波那契数列

斐波那契数列：数列的第0项为0，第1项为1，之后的每一项等于其前两项的和

例：

递推关系：

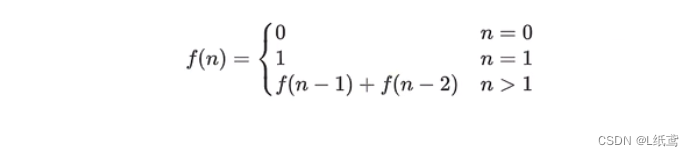
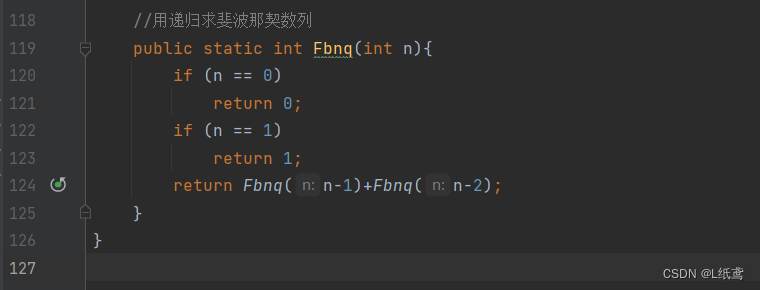
代码实现：求斐波那契数列第n项的值

注意：

我们之前的例子是每个递归函数只包含一个自身的调用，这称之为单路递归；如果每个递归函数里包含多个自身调用，称之为多路递归。

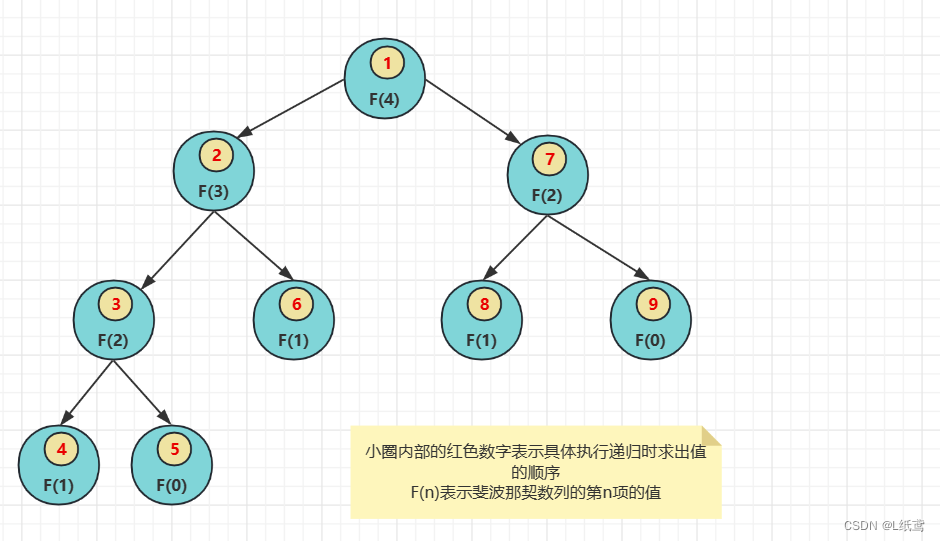
下面分析一个上述代码的递归过程：

斐波那契数列的时间复杂度：

斐波那契数列的时间复杂度就是你递归了多少次，即你调用了多少次函数。这个由上图可以看出，求斐波那契数列的第四项时，调用了9次函数，当n取不同值的时候，自己可以算一算。

直接给出结论：

8.用递归解决兔子问题

兔子问题是斐波那契数列的经典问题。

问题描述：

第一个月，有一对未成熟的兔子。第二个月，它们成熟，第三个月，它们能产下一对新兔子；所有的兔子都遵循这个规律，求第n个月的兔子数。

具体分析：

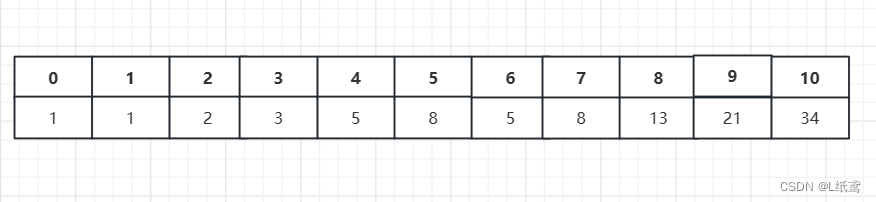
我们假设求第 n 个月的兔子数。第 n 个月的时候，第n-2个月的兔子已经成熟，会生下新的兔子，所以，第 n 个月时的兔子数包含第n-2个月的兔子数。除此之外，还有上个月存活的兔子数。这个怎么理解？我们可以这样想，第n-2个月时，有a个兔子，第n-1个月时，有n-2个月的兔子和新产生的兔子，第n个月时就有第n-1个月的兔子和新产生的兔子，而这新产生的兔子是由第n-2个月的兔子生下的，所以第n个月的兔子=第n-2个月的兔子+第n-1个月的兔子，这就是递推关系。

下面看一下代码实现：

9.用递归解决青蛙爬楼梯问题

问题描述：

楼梯有n阶，青蛙要爬到楼顶，可以一次跳一阶，也可以一次跳两阶，并且只能向上跳，问有多少种跳法。请输入楼梯阶数，输出跳法种数。

问题分析：

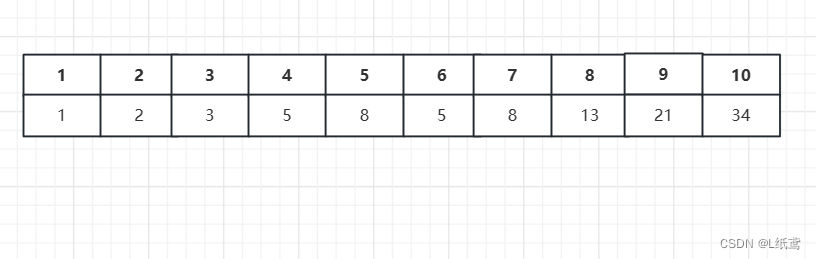
假设青蛙跳n阶，因为青蛙一次只能跳一阶或两阶。如果青蛙最后跳1阶，那么它就是从第n-1阶开始跳的，第n-1阶有多少种跳法，那么青蛙最后跳一阶这种就有多少种跳法，因为只需要最后跳一下就可以了。同理，如果青蛙最后跳2阶，那么它就是从第n-2阶开始跳的，第n-2阶有多少种跳法，那么青蛙最后跳2阶这种就有多少种跳法，因为只需要最后跳2阶就可以了。

这样递推关系就出来了，第n阶跳法 = 第n-1阶跳法+第n-2阶跳法。

代码实现：

10.递归问题的优化

上面，我们提到，递归问题的时间复杂度为：

时间复杂度这么高的原因是递归的次数多，即你自我调用的次数太多了。斐波那契数列的时间复杂度就是你递归了多少次，即你调用了多少次函数。

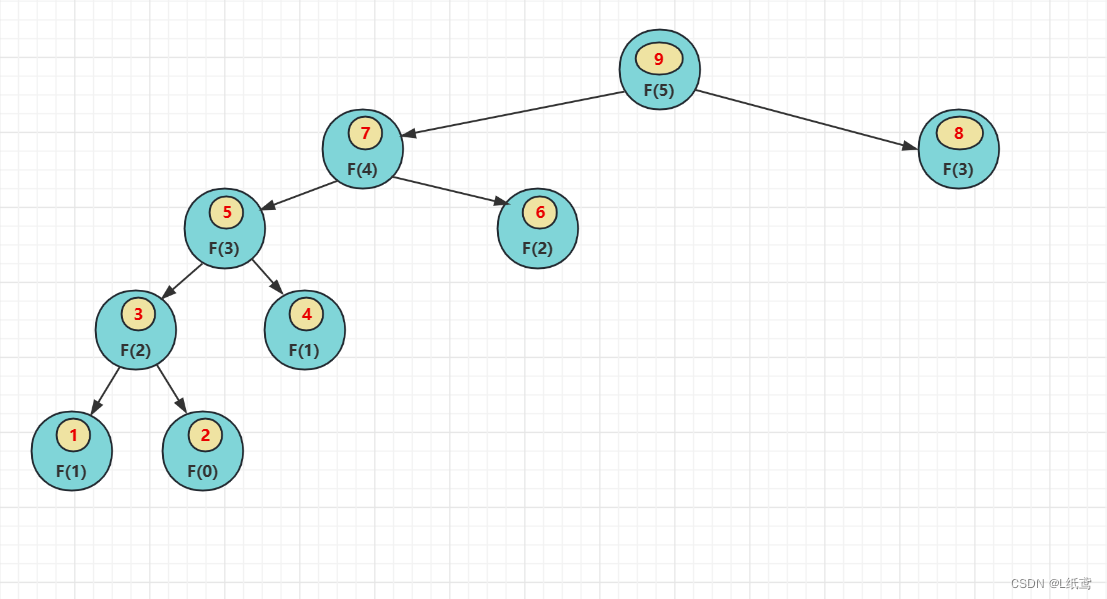
下面来分析一下求出 f（5）的具体流程：

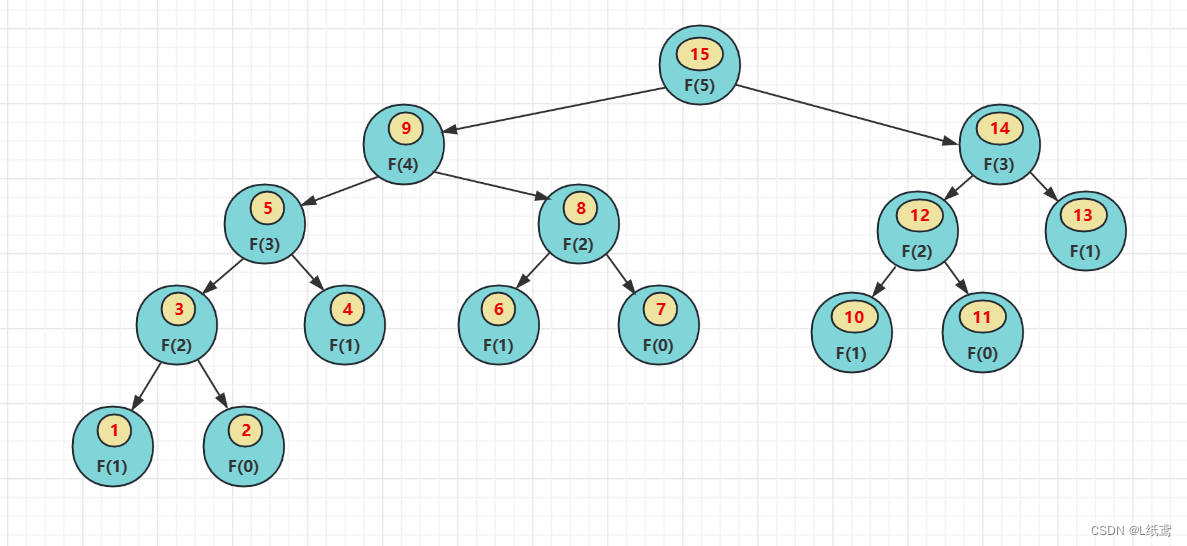
具体流程：

要求 f（5），就要调用 f（n-1）即 f（4），要求 f（4）就要求 f（3），要求 f（3）就要求 f（2），要求 f（2）就要求 f（1），现在 f（1）知道了，然后求 f（0），f（0）也知道了，所以 f（2）知道了，要求 f（3），有了 f（2），还要求 f（1），f（1）知道了，所以 f（3）知道了，此时 f（3）知道了，要求 f（4），还要知道 f（2），然后再走一遍上面求 f（2）的调用过程，到这里就能看出来，不必要重复的调用太多了，就是因为这种复杂的重复调用导致斐波那契数列的时间复杂度极高。

其实由上图也能看出，求 f(5) 时，右边支即求 f(3) 的那个分支和求 f(4)时的左边支完全一样，又重复了一遍求 f(3) 的过程，是属于重复操作。

为什么会重复这样？因为我们不知道他们的值，只知道 f(0) 和 f（1）的值，所以要求一个新值时，就要重复递归，回到 f（0）和 f（1）处，然后根据这个两个值求出新值。

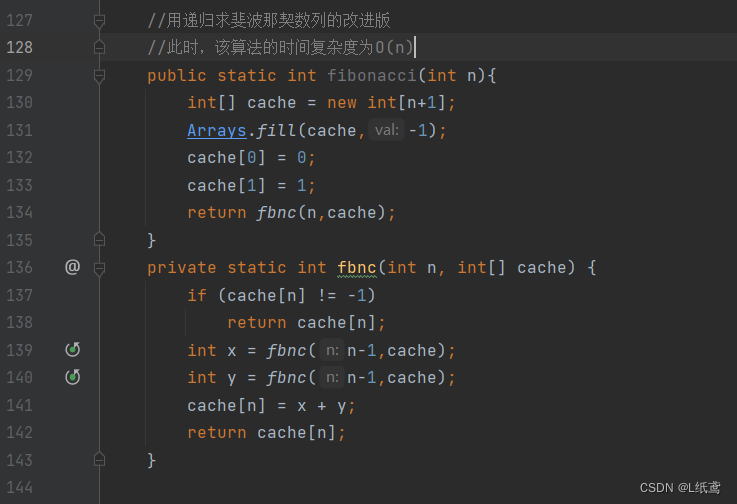
那怎么解决？我们是否可以多记录几个值？比如记录10个值，可以是可以，求f（11）时可以，但是当求f（1000）时，还是有很多的递归。治标不治本。

前面说了，重复调用的原因是不知道新的值，即值太少，导致会重复求一些值，就是会重复求一些值。重新说一下，上面重复递归的原因就是会重复求一些值。怎么才能不重复求？把已经求的记录下来？怎么记录？用数组记录。数组初始有什么？有 f(0) 和 f(1) 的值，然后每次递归需要求出一个值时，先看数组中有没有，如果有，直接用数组中的，如果没有，再递归求，求完后将这个值写入数组中存储起来，方便后续的使用。这就是解决方法！

那么按照这个方法，上图可以画为：

代码实现如下所示：

11.递归问题的爆栈问题

下面来看一下递归的爆栈问题

假设，我们需要进行递归求和，即求前n项的和，下面看一下代码：

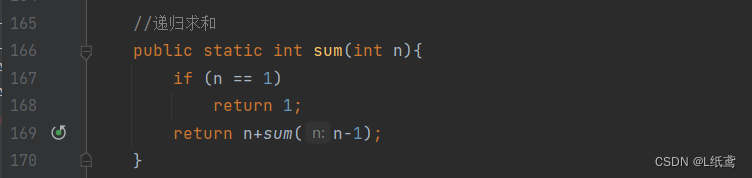
求sum(100)，得出答案5050，求sum（20000），就会报下面的错误：

这就是一个爆栈问题。

下面分析一下：

java程序在运行时会占用空间的， 方法的调用会执行入栈操作，一直到方法运行结束，才会执行出栈操作。栈的内存空间大小是一定的，当栈内的方法满了的时候，再调用方法就无法入栈了，也就是会爆栈了。而上述递归就是一个不断调用函数的过程，因为调用的函数太多，并且没有执行到递归结束，所以就出现了爆栈现象。

怎么解决？目前的解决的解决方案就是尽量控制递归的次数少一点。

下面看一下尾调用：

Java的编译器不支持这种优化，支持这种优化的语言有C++，Scala等

12.递归的时间复杂度计算

下面看一下递归的时间复杂度计算

前面只是稍微讲了一下用递归求斐波那契数列的时间复杂度，属于具体问题具体分析了，下面讲一下求一般递归问题的时间复杂度的计算方法

方法一：Master theorem主定理法（符合公式就直接套公式算）

看几个例子：

具体分析一下递归版二分查找的时间复杂度：

具体分析一下归并排序的时间复杂度：

具体分析一下快速排序的时间复杂度：

方法二：展开求解

这种方法一般是递归不符合方法一中的公式的时候，才会用的，需要一定的数学功底。

大家可以好好分析这两个例子

13.用递归求解汉诺塔问题

汉诺塔问题：

Tower of Hanoi，是源于印度的古老传说，大梵天创建世界的时候做了三根金刚石柱，在一根柱子从下往上按大小顺序摞着64片黄金圆盘，大梵天命令婆罗门把圆盘重新摆放在另一根柱子上，并且规定：

一次只能移动一个圆盘
小圆盘上不能放大圆盘

要求：用代码模拟圆盘的移动过程，并且估算时间复杂度

解析：对于移动n个圆盘，我们可以考虑前面n-1个圆盘是移动好的，只需要思考前n-1个圆盘和第n个圆盘要如何移动。

代码实现：

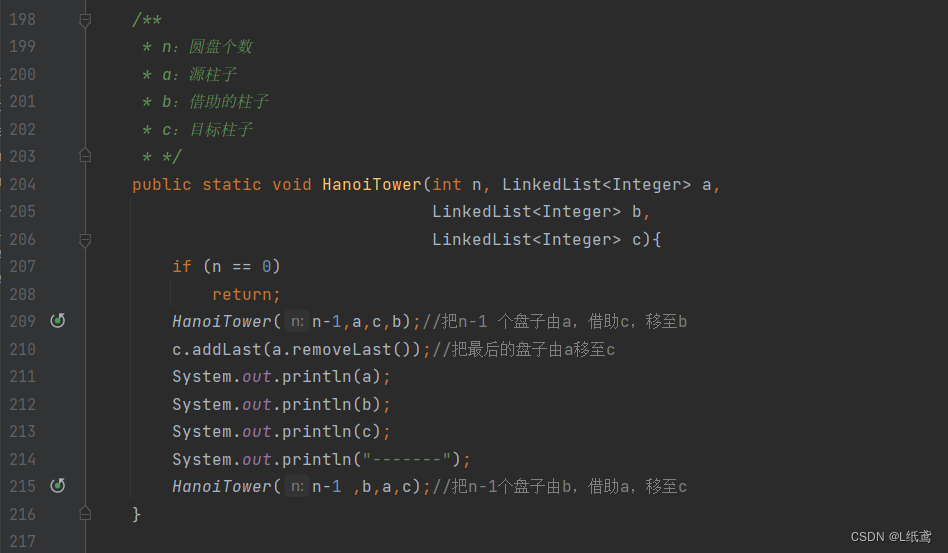
时间复杂度：O(2^n)

14.用递归求解杨辉三角问题

杨辉三角形如下图所示：

它的每个元素等于该元素正上方的两个元素之和

要求：输入元素的坐标，返回元素的值

分析：

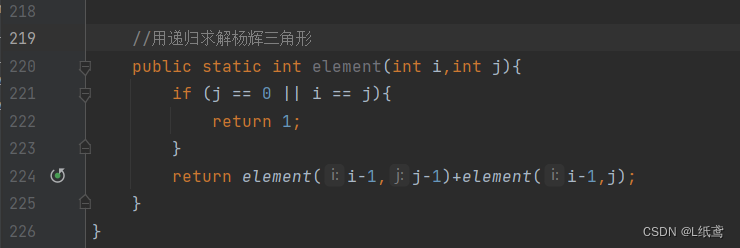
代码实现：

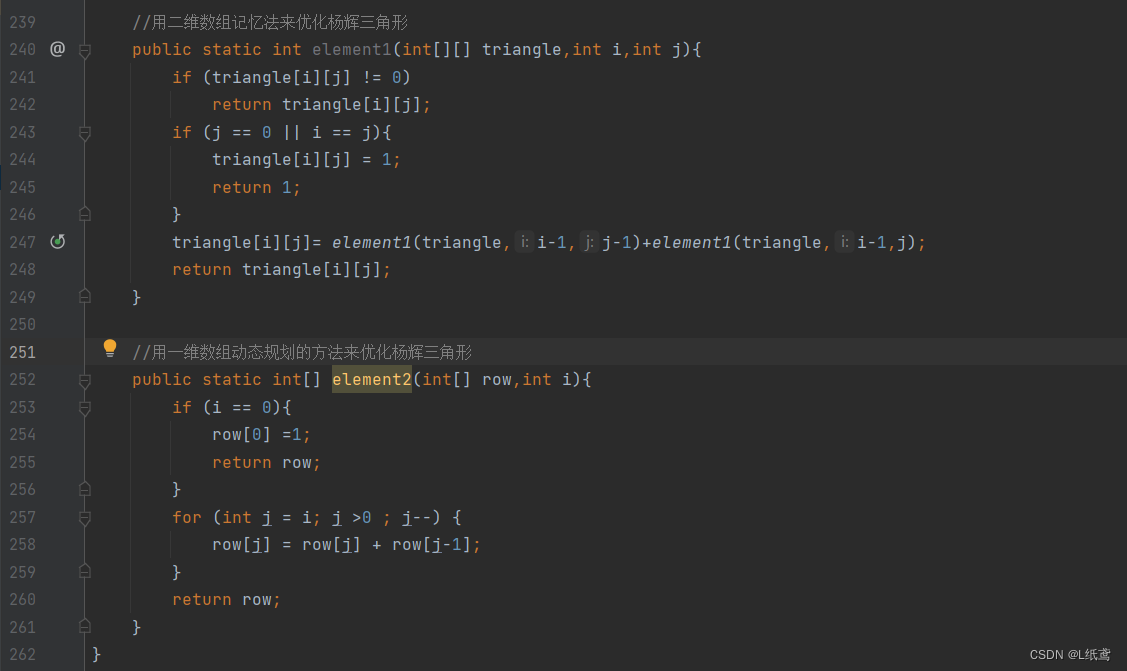
代码优化：

15.小结

递归的讲解至此就告一段落。

小结一下递归的思想和解题技巧：

当一个问题的解决方法出现循环的现象时，我们要找其最小子问题，然后分析解决方法中的循环部分
最小子问题不好找的时候，我们可以先分析解决方法的循环部分，把循环的这部分先写出来
递归最后一定要分析递归的终点，即递归到什么时候结束
对一些比较过程比较复杂的问题时，我们可以简化操作，将前n-1步看成已经处理好的，考虑第n-1步和n步之间的关系，然后再往前思考（青蛙问题、汉诺塔问题），这其实也是一种分治的思想
多路递归常常会和分治联合在一起出现
对于一个问题，我们可以这样做：先整体思考（大），想不出来再分析本质（小），想不出来再分开想（中）（个人观点，暂时就这么多，以后题做多了再总结）

最后附上递归练习（本文中出现的）的源码：


import java.util.Arrays;
import java.util.LinkedList;

/**
 * 递归函数的实现与练习
 *
 * */
public class L6_Factorial {
    public static void main(String[] args) {
        
        //没写测试类，就在主方法中测试了写的一些方法

        //System.out.println(f(3));
        //s("ABIDE",0);

        //int[] arr = {6,11,12,19,26,27,30,37};
        //int index = BinarySearch(arr,37,0, arr.length-1);
        //System.out.println(index);

        //int[] arr = {18,6,2,74,23,11,9,1};
        //EffervescenceSort(arr,arr.length-1);
        //InsertSort(arr,1);
        //System.out.println(Arrays.toString(arr));

        //System.out.println(Fbnc1(8));
        //System.out.println(sum(20));

        //System.out.println(money(1000000000L));

//        LinkedList<Integer> a = new LinkedList<Integer>();
//        LinkedList<Integer> b = new LinkedList<Integer>();
//        LinkedList<Integer> c = new LinkedList<Integer>();
//        a.addLast(3);
//        a.addLast(2);
//        a.addLast(1);
//        HanoiTower(3,a,b,c);

//        System.out.println(element(4, 2));

//        int[][] a = new int[10][10];
//        System.out.println(element1(a, 4, 2));

        int[] row = new int[5];
        for (int i = 0; i < 5; i++) {
            element2(row,i);
        }
        System.out.println(Arrays.toString(row));

    }

    //用递归求阶乘
    public static int f(int n){
        if (n == 1)
            return 1;
        return n*f(n-1);
    }

    //用阶乘反转字符串
    public static void s(String str,int n){
        if (n == str.length())
            return;
        s(str,n+1);
        System.out.print(str.charAt(n));
    }

    //用递归求解二分查找
    public static int BinarySearch(int[] arr,int target,int left,int right){
        //这里不能加=，防止目标值在i和j处
        if(left > right)
            return -1;
        int mid = (left+right)>>>1;
        if (arr[mid] < target)
            return BinarySearch(arr,target,mid+1,right);
        else if(target < arr[mid])
            return BinarySearch(arr,target,left,mid-1);
        else
            return mid;
    }

    //用递归解决冒泡排序
    public static void EffervescenceSort(int[] arr,int j){
        if (j == 0)
            return;
        for (int i = 0; i < j; i++) {
            if (arr[i] > arr[i+1]){
                int t = arr[i];
                arr[i] = arr[i+1];
                arr[i+1] = t;
            }
        }
        EffervescenceSort(arr,j-1);
    }
    //用递归解决冒泡排序改进版(减少一些不必要的递归)
    public static void EffervescenceSortBetter(int[] arr,int j){
        if (j == 0)
            return;
        int x = 0;
        for (int i = 0; i < j; i++) {
            if (arr[i] > arr[i+1]){
                int t = arr[i];
                arr[i] = arr[i+1];
                arr[i+1] = t;
                x = i;
            }
        }
        EffervescenceSort(arr,x);
    }

    //用递归实现插入排序
    public static void InsertSort(int[] arr,int low){
        if (low == arr.length)
            return;
        int t = arr[low]; //定义变量暂时记录插入的元素
        int i = low-1;    //已排好序的尾边界指针
        while (i>=0 && arr[i] > t){ //没有找到插入位置
            arr[i+1] = arr[i];//空出插入位置
            i--;
        }
        //找到插入位置
        if (i+1 != low)
            arr[i+1] = t;
        InsertSort(arr,low+1);
    }

    //插入排序的另一种递归实现方法
    public static void InsertSort1(int[] a,int low){
        if (low == a.length)
            return;

        int i = low-1;
        while (i >=0 && a[i] > a[i+1]){
            int t = a[i];
            a[i] = a[i+1];
            a[i+1] = t;

            i--;
        }
        InsertSort1(a,low+1);
    }

    //用递归求斐波那契数列
    public static int Fbnc1(int n){
        if (n == 0)
            return 0;
        if (n == 1)
            return 1;
        return Fbnc1(n-1)+Fbnc1(n-2);
    }

    //用递归求斐波那契数列的改进版
    //此时，该算法的时间复杂度为O(n)
    public static int fibonacci(int n){
        int[] cache = new int[n+1];
        Arrays.fill(cache,-1);
        cache[0] = 0;
        cache[1] = 1;
        return fbnc(n,cache);
    }
    private static int fbnc(int n, int[] cache) {
        if (cache[n] != -1)
            return cache[n];
        int x = fbnc(n-1,cache);
        int y = fbnc(n-1,cache);
        cache[n] = x + y;
        return cache[n];
    }


    //用递归求斐波那契数列的变形问题——不死神兔
    public static int rabbit(int n){
        if (n == 0)
            return 1;
        if (n == 1)
            return 1;
        return rabbit(n-1)+rabbit(n-2);
    }

    //用递归求斐波那契数列的变形问题——青蛙跳台阶
    public static int frog(int n){
        if (n == 1)
            return 1;
        if (n == 2)
            return 2;
        return rabbit(n-1)+rabbit(n-2);
    }

    //递归求和
    public static int sum(int n){
        if (n == 1)
            return 1;
        return n+sum(n-1);
    }

    //将一个数转为金钱计数法形式，例10000000 --> 10,000,000，这里没用递归，只是一个练习
    public static String money(Long a){
        String b = String.valueOf(a);
        String c = "";
        int j = 1;
        for (int i = b.length()-1;i>=0;i--,j++){
            if (j%3 == 0 && j<b.length()){
                c =","+ b.charAt(i)+c;
            }else
                c = b.charAt(i)+c;
        }
        return c;
    }
    /**
     * 用递归求解汉诺塔问题
     * n：圆盘个数
     * a：源柱子
     * b：借助的柱子
     * c：目标柱子
     * */
    public static void HanoiTower(int n, LinkedList<Integer> a,
                                  LinkedList<Integer> b,
                                  LinkedList<Integer> c){
        if (n == 0)
            return;
        HanoiTower(n-1,a,c,b);//把n-1 个盘子由a，借助c，移至b
        c.addLast(a.removeLast());//把最后的盘子由a移至c
        System.out.println(a);
        System.out.println(b);
        System.out.println(c);
        System.out.println("-------");
        HanoiTower(n-1 ,b,a,c);//把n-1个盘子由b，借助a，移至c
    }

    //用递归求解杨辉三角形
    public static int element(int i,int j){
        if (j == 0 || i == j){
            return 1;
        }
        return element(i-1,j-1)+element(i-1,j);
    }

    //用二维数组记忆法来优化杨辉三角形
    public static int element1(int[][] triangle,int i,int j){
        if (triangle[i][j] != 0)
            return triangle[i][j];
        if (j == 0 || i == j){
            triangle[i][j] = 1;
            return 1;
        }
        triangle[i][j]= element1(triangle,i-1,j-1)+element1(triangle,i-1,j);
        return triangle[i][j];
    }

    //用一维数组动态规划的方法来优化杨辉三角形
    public static int[] element2(int[] row,int i){
        if (i == 0){
            row[0] =1;
            return row;
        }
        for (int j = i; j >0 ; j--) {
            row[j] = row[j] + row[j-1];
        }
        return row;
    }
}

L纸鸢

关注

1
点赞
踩
6

收藏

觉得还不错? 一键收藏
打赏
0
评论
数据结构与算法——11.递归

在计算机科学中，递归是一种解决计算问题的方法，其中解决方案取决于同一类问题的更小子集。return;上述代码的特点是在函数内部自己调用了自己，如果我们把每个函数看成是某一种问题的解决方法，自己调用自己说明下次的这个调用还是解决这个问题，说明函数解决的是同一类问题。如果这个函数中调用了别的函数，那么就说明你解决的不是同一类问题了，这就不是递归了（其实还是有的绕，不是很清楚）每次调用，函数处理的数据会较上次缩减（子集），而且最后会缩减至无需递归。
复制链接

扫一扫