集成聚类经典之作

[16]Robust Ensemble Clustering Using Probability Trajectories(PTA、PTGP)

首次提出微簇（microclusters）的概念，以及基于微簇的CA矩阵MCA来衡量微簇之间的共现性。

1.MCA（microcluster based co-asscoiation）矩阵记录了在m个基结果中，每两个微簇出现在同一个簇中的频率。即微簇的共现性。

2.Elite Neighbor Selection保留少部分高置信度的连接 得到稀疏图W，然后执行随机游走得到稠密图，其中转移概率矩阵Q考虑了微簇的大小。基于此可以得到T步的随机游走的概率轨迹R，probability trajectory similarity（PTS）是通过计算两个微簇间的概率轨迹的cos相似性得到，矩阵衡量了微簇间的相似性，可以被当做增强的CA矩阵。聚类结果可由微簇映射回样本得到。

通过概率轨迹（probability trajectory）来利用多步信息来描述随机游走过程

【17】Spectral Ensemble Clustering via Weighted K-Means（SEC）

【18】LWEA（Local Weighted Ensemble Clustering）

利用聚类的不确定性和局部多样性来精炼CA矩阵

通过熵 来衡量聚类的不确定性

通过其来计算ECI（Ensemble-driven Cluster index）作为CA矩阵的融合的权重

增强的CA矩阵：

【19】Ensemble clustering based on dense representation(DREC)

通过提取微簇得到C，然后计算其相似性矩阵。

【21】Enhanced Ensemble Clustering via Fast Propagation of Cluster-Wise Similarities（ECPCS）

使用Jaccard系数来衡量簇间相似性，并加入高阶信息 得到簇级相似性图Z 用来增强CA矩阵

如果xi和xj所属簇不同的话，bij为两个簇的相似性，由此ECA可以捕捉到它们的不直接关系。

之后可以使用层次聚类（Hierarchical Clusteirng）在目标级划分 或元聚类（meta clusteirng）在簇级划分。

A.层次聚类通过不断将相似性大的区域进行融合，形成一颗树结构（HC tree）

B.元聚类

【21】Tri-level Robust Clustering Ensemble with Multiple Graph Learning（TRCE）

整合了基聚类级、图级以及实例级的信息

[22]Towardes Multidiversified Ensemble Clustering of High-Dimensional Data:From Subspace to Metrics and Beyond（MDEC）

本文使用随机核函数、随机子空间来增强多样性。之后通过SC获得基聚类，利用簇级相似性得到Local Weighted CA矩阵。最后使用了三种共识函数HC、SC和BG获得最终结果。

1.随机选择超参u和k

2.随机进行子空间特征采样，即从原始数据随机采样特定的特征作为其子空间达到低维。

3.通过M次随机的核函数，随机子空间，获得M个metric-subspace pairs

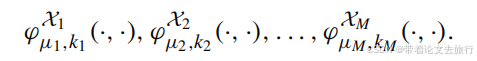
相似性矩阵的获得 就是先将xi 和xj投影到低维，然后计算它们的核相似性。有了相似性矩阵就可以构造图，利用谱聚类划分得到基结果。