（PTA）数据结构（作业）8、期中测验

原创已于 2022-10-07 11:54:48 修改 · 4.8k 阅读

50 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #链表 #c++ #算法

于 2022-05-09 16:35:13 首次发布

数据结构专栏收录该内容

16 篇文章

订阅专栏

本文探讨了如何使用编程实现单链表中偶数个数的计数和链式表的长度计算，涉及循环队列、链表操作时间复杂度以及栈和队列数据结构的应用。

判断题

1、所谓“循环队列”是指用单向循环链表或者循环数组表示的队列。 F

循环队列本身是一种顺序存储结构，不是链式存储结构。

将顺序队列变成一个环状的空间（即队列首尾相连），这样的队列称为循环队列。

循环队列是利用了模运算的方式来实现“循环”移动。

2、在具有N个结点的单链表中，访问结点和增加结点的时间复杂度分别对应为O(1)和O(N)。 F

在单链表中，访问（增加）前驱结点需要从头开始顺序访问，而访问（增加）后继结点只需要进行一次间接寻址的操作。

因此，访问某节点的前驱节点的时间复杂度为O(N)，访问其后继节点的时间复杂度为O(1)。增加其前驱节点的时间复杂度为O(N)，增加其后继节点的时间复杂度为O(1)。

3、对于顺序存储的长度为N的线性表，访问结点和增加结点的时间复杂度分别对应为O(1)和O(N)。 T

4、若一个栈的输入序列为{1, 2, 3, 4, 5}，则不可能得到{3, 4, 1, 2, 5}这样的出栈序列。 T

5、对于顺序存储的长度为N的线性表，删除第一个元素和插入最后一个元素的时间复杂度分别对应为O(1)和O(N)。 F

对于顺序存储的线性表，在删除第一个元素的操作确实是O(1)，但是还要将其进行重新排列，即后边的元素前移，所以删除第一个元素的时间复杂度是O(N)，而插入最后一个元素可以根据索引直接找到目标位置，所以是O(1)。

6、算法分析的两个主要方面是时间复杂度和空间复杂度的分析。 T

7、In a circular queue which is implemented by an array, the front value must always be no larger than the rear value. F

在由数组实现的循环队列中，front必须始终不大于rear。

rear可以因为循环的原因移动到开头，所以front不一定不大于rear。

8、若用链表来表示一个线性表，则表中元素的地址一定是连续的。 F

链表的地址不一定是连续的，它们之间是依靠指针链接的。

9、若某线性表最常用的操作是存取任一指定序号的元素和在最后进行插入和删除运算，则利用顺序表存储最节省时间。 T

10、在用数组表示的循环队列中，front值一定小于等于rear值。 F

rear可以因为循环的原因移动到开头，所以front不一定小于等于rear。

选择题

1、设h为不带头结点的单向链表。在h的头上插入一个新结点t的语句是：

A.t->next=h->next; h=t;

B.t->next=h; h=t;

C.h=t; t->next=h->next;

D.h=t; t->next=h;

2、线性表( $a_1,a_2,...,a_n$ )以顺序存储结构存储时，访问第i位置元素的时间复杂度为（）

A.O(n)

B.O(1)

C.O(i-1)

D.O(i)

3、为解决计算机主机与打印机之间速度不匹配问题，通常设置一个打印数据缓冲区，主机将要输出的数据依次写入该缓冲区，而打印机则依次从该缓冲区中取出数据。该缓冲区的逻辑结构应该是？

A.树

B.堆栈

C.队列

D.图

4、设计一个判别表达式中左，右括号是否配对出现的算法，采用（）数据结构最佳

A.链表

B.顺序表

C.栈

D.队列

5、假设有5个整数以1、2、3、4、5的顺序被压入堆栈，且出栈顺序为3、5、4、2、1，那么为了获得这样的输出，堆栈大小至少为：

A.3

B.4

C.2

D.5

6、在具有N个结点的单链表中，实现下列哪个操作，其算法的时间复杂度是O(N)？

A.删除开始结点

B.在地址为p的结点之后插入一个结点

C.遍历链表和求链表的第i个结点

D.删除地址为p的结点的后继结点

7、现有队列 Q 与栈 S，初始时 Q 中的元素依次是{ 1, 2, 3, 4, 5, 6 }（1在队头），S 为空。若允许下列3种操作：（1）出队并输出出队元素；（2）出队并将出队元素入栈；（3）出栈并输出出栈元素，则不能得到的输出序列是：

A.6, 5, 4, 3, 2, 1

B.1, 2, 5, 6, 4, 3

C.2, 3, 4, 5, 6, 1

D.3, 4, 5, 6, 1, 2

8、如果循环队列用大小为m的数组表示，队头位置为front、队列元素个数为size，那么队尾元素位置rear为：

A.(front+size-1)%m

B.(front+size)%m

C.front+size

D.front+size-1

9、顺序表中第一个元素的存储地址是100，每个元素的长度为2，则第5个元素的地址是（）。

A.108

B.110

C.100

D.105

10、给定一个堆栈的入栈序列为{ 1, 2, ⋯, n }，出栈序列为{ p1, p2, ⋯, pn }。如果p2=n，则存在多少种不同的出栈序列？

A.1

B.n

C.2

D.n−1

11、利用栈实现十进制整数1234转八进制，以下哪项栈表状态符合实际情况：

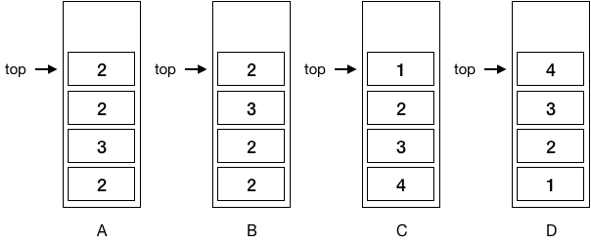
A.B

B.C

C.A

D.D

12、若一个栈的入栈序列为1、2、3、…、N，其输出序列为p1、p2、p3、…、pN。若p1=N，则pi为：

A.n−i

B.i

C.n−i+1

D.不确定
当出栈的第一个元素（N）刚好是入栈顺序（1,2,3,...,N）的最后一个元素，那么说明它前面的元素(1,2,3,...N-1)已经全部进栈了，那么出栈的顺序就已经定死了，必须是N,N-1,N-2,...3,2,1。如第一个，n-1+1=n,第二个n-2+1=n-1;所以就可以根据规律第i个元素为n-i+1,

13、若一个栈的入栈序列为1、2、3、…、N，输出序列的第一个元素是i，则第j个输出元素是：

A.i−j−1

B.i−j

C.不确定

D.j−i−1

这道题和上一道题的区别在于第一个输出的元素是i，而不是最后一个元素，因此之后可以是入栈出栈操作交叉出现，所以不能确定输出元素。

14、带头结点的单链表h为空的判定条件是：

A.h == NULL;

B.h->next == h;

C.h != NULL;

D.h->next == NULL;

15、在N个结点的顺序表中，算法的时间复杂度为O(1)的操作是：

A.访问第i个结点（1≤i≤N）和求第i个结点的直接前驱（2≤i≤N）

B.在第i个结点后插入一个新结点（1≤i≤N）

C.删除第i个结点（1≤i≤N）

D.将N个结点从小到大排序

BC插入和删除需要移动n-i个节点，因此为O(n)
根据排序方法不同最慢O(n^2)，最快O(nlogn)

16、从栈顶指针为ST的链栈中删除一个结点且用X保存被删结点的值，则执行：

A.X= ST; ST = ST->next;

B.X= ST->data; ST = ST->next;

C.ST = ST->next; X= ST->data;

D.X= ST->data;

17、不带头结点的单链表（头指针为head）为空的判定条件是（）

A.head!=NULL

B.head->next==NULL

C.head->next=head

D.head==NULL

18、线性表若采用链式存储结构时，要求内存中可用存储单元的地址

A.连续或不连续都可以

B.部分地址必须是连续的

C.一定是不连续的

D.必须是连续的

19、若已知一队列用单向链表表示，该单向链表的当前状态（含3个对象）是：1->2->3，其中x->y表示x的下一节点是y。此时，如果将对象4入队，然后队列头的对象出队，则单向链表的状态是：

A.4->1->2

B.1->2->3

C.答案不唯一

D.2->3->4

20、对于一个具有N个结点的单链表，在给定值为x的结点后插入一个新结点的时间复杂度为

A.O(N/2)

B.O(1)

C.O( $N^2$ )

D.O(N)

填空题

下列代码的功能是返回带头结点的单链表L的逆转链表。

List Reverse( List L )
{
    Position Old_head, New_head, Temp;
    New_head = NULL;
    Old_head = L->Next;

    while ( Old_head )  {
        Temp = Old_head->Next;
        
        Old_head->Next = New_head; //填空
 
        New_head = Old_head;  
        Old_head = Temp; 
    }
    
    L->Next = New_head;//填空
    return L;
}

分析：

逆转链表，其实跟头插法很像，不过插入的过程中需要用临时变量来保存还没逆转部分的头结点的下一个结点。

新的头结点是逆转后的链表的头结点，而一开始的时候是没逆转的，

所以新头结点为空，

然后再新头结点前边插入一个又一个结点，从而形成逆转后的链表。

因为带头结点，所以第一个有数据的元素是L->Next。

先用临时变量保存旧头结点的下一个元素，然后将旧的头结点前插到新头结点前方，

即Old_head->Next = New_head;

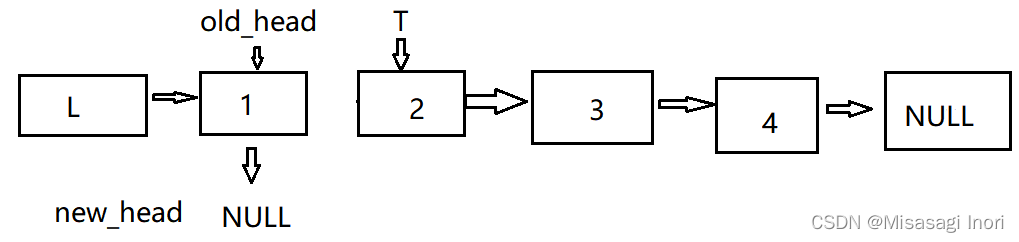
新头结点要移动到新链表的前方，此时新链表的头结点是Old_head，

所以New_head = Old_head;

然后旧头结点通过临时变量移动到旧链表的下一个元素。

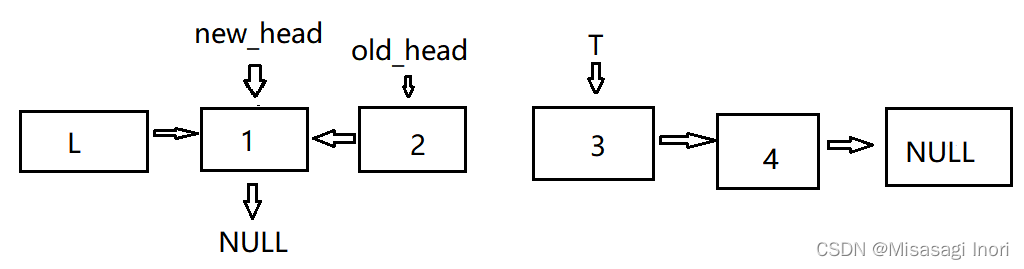
当旧头结点指向空的时候，说明链表逆转结束，此时将原本链表的头结点L跟新的链表的头结点相连，即 L->Next = New_head;

此时就是逆转后的带头结点的链表。

编程题

R6-1 单链表统计偶数个数

本题要求实现一个函数，返回带头结点的单链表中偶数的个数。

函数接口定义：

int EvenNumber(LinkList L);

L是带头结点的单链表的头指针，函数EvenNumber返回L中偶数的个数。如果单链表为空，返回0。

其中LinkList结构定义如下：

typedef struct LNode
{
    ElemType data;
    struct LNode *next;
}LNode,*LinkList;

裁判测试程序样例：


#include <stdio.h>
#include <stdlib.h>

typedef int ElemType;
typedef struct LNode
{
    ElemType data;
    struct LNode *next;
}LNode, *LinkList;

LinkList Create();/* 细节在此不表 */

int EvenNumber(LinkList L);
int main()
{
    LinkList L, p;
    ElemType e;
    L = Create();
    printf("Even number is %d.\n", EvenNumber(L));
    return 0;
}
/* 你的代码将被嵌在这里 */

输入格式：

输入数据为1行，给出以-1结束的单链表元素（-1不属于单链表元素），所有数据之间用空格分隔。

输入样例：

6 -3 4 -5 3 -1

输出样例：

Even number is 2.

参考答案：

int EvenNumber(LinkList L)
{
    LNode *p;
    int sum=0;
    p=L->next;
    while(p!=NULL)
    {
        if(p->data%2==0)
        {
            sum ++;
        }
        p=p->next;
    }
    return sum;
}

R6-2 求链式表的表长

本题要求实现一个函数，求链式表的表长。

函数接口定义：

int Length( List L );

其中List结构定义如下：

typedef struct LNode *PtrToLNode;
struct LNode {
    ElementType Data;
    PtrToLNode Next;
};
typedef PtrToLNode List;

L是给定单链表，函数Length要返回链式表的长度。

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>

typedef int ElementType;
typedef struct LNode *PtrToLNode;
struct LNode {
    ElementType Data;
    PtrToLNode Next;
};
typedef PtrToLNode List;

List Read(); /* 细节在此不表 */

int Length( List L );

int main()
{
    List L = Read();
    printf("%d\n", Length(L));
    return 0;
}

/* 你的代码将被嵌在这里 */

输入样例：

1 3 4 5 2 -1

输出样例：

参考答案：

int Length(List L)
{
    int sum=0;
    while(L!=NULL)
    {
        sum ++;
        L =L->Next;
    }
    return sum;
}