方程与方程组的解析解和数值解

目录

 

1.1 方程和方程组的解析解（solve）

1.2 方程和方程组的数值解（fsolve）

---

1.1 方程和方程组的解析解（solve）

solve函数的用法 :solve(方程1，方程2……，变量1，变量2……)

多项式合并 ： （x+3x-5x）x/4

syms x   % 指定x为符号变量 
(x+3*x-5*x)*x/4

 方程1：

 

syms a b c x
y = a*x^2+b*x+c;
solve(y,x)  % solve(方程，变量)

 

 

 

syms x
y = 2*x-x^2-exp(-x);
solve(y,x)

 

 

syms x b y a
y1 = x+b*y-5;
y2 = a*x-y-x;
res = solve(y1,y2,x,y)
% 上面返回结构体  
% res.  查看x y 的值
res.x 
res.y 

 

 

 

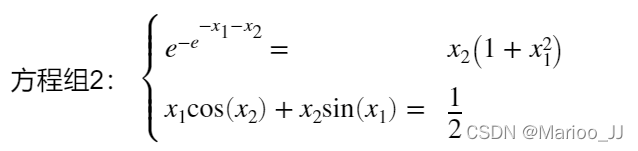
syms x1 x2
y1 = exp(-exp(-x1-x2))-x2*(1+x1^2);
y2 = x1*cos(x2) + x2*sin(x1)-1/2;
res = solve(y1,y2,x1,x2);
res.x1
res.x2

 

1.2 方程和方程组的数值解（fsolve）

fsolve函数用法 ： fsolve(函数句柄，初值)

初值 一般是通过经验给出

 

 

方程：2*x-x^2=e^(-x)

f = @(x)2*x-x^2-exp(-x)
fsolve(f,0)  % f是函数句柄  0是函数初值（牛顿迭代法）

 

% 普通函数转化成匿名函数
a=3;
b=5;
f = @(x)funs(x,a,b);
fsolve(f,[0,0])

function y = funs(x,a,b) % x = [x,y]
   y(1) = x(1)+ b*x(2)-5;
   y(2) = a*x(1) -x(2) -x(1);
end

 

 

f = @fun;
fsolve(f,[0,0])


function y = fun(x)  % x =[x1,x2]
  y(1) = exp(-exp(-x(1)-x(2)))-x(2)*(1+x(1)^2);
  y(2) = x(1)*cos(x(2)) + x(2)*sin(x(1))-1/2;
end