算法设计与分析概述部分期末复习

算法概述

算法概述

算法的特征(5个）

1. 输入（input）：算法有零个或多个输入量；
2. 输出（output）：算法至少产生一个输出量；
3. 确定性（definiteness）：算法的每一条指令都有确切的定义，没有二义性；
4. 能行性（effectiveness）：算法的每一条指令必须足够基本，可以通过已经实现的基本运算执行有限次来实现；
5. 有穷性（finiteness）：算法必须总能在执行有限步之后终止。

程序与算法

1. 程序是算法用某种程序设计语言的具体实现。
2. 程序可以不具有有穷性。
3. 操作系统是一个在无限循环中执行的程序，不是算法。

算法设计过程*

1. 理解问题
2. 预测所有可能的输入
3. 在精确解和近似解之间间做选择
4. 确定适当的数据结构
5. 算法设计技术:贪心法、分治法、动态规划法等
6. 描述算法
7. 跟踪算法
8. 分析算法效率
9. 根据算法编写代码

算法分类

1. 精确算法（exact algorithm）总能保证求得问题的解
2. 启发式算法（heuristic algorithm）通过使用某种规则、简化或智能猜测来减少问题求解时间
3. 近似算法（approximation algorithm)，致力于寻找最优化问题的近似解而不是最优解
4. 随机算法（randomized algorithm)，在算法中需做出某些随机选择

算法验证与分析

1. 算法验证：确认一个算法是否正确
   1. 算法证明：使用数学方法证明算法的正确性
   2. 程序测试：输入样本数据(测试用例)，检查输出
2. 算法分析：对算法的执行时间和所需空间的估算
   1. 性能测量：也可使用样本数据，实际测量一个程序所消耗的时间和空间

程序性能

程序性能

指程序运行时所需的内存空间量和计算时间:系统开销和求解问题本身的开销.
忽略系统开销,区分出算法的性能.
本课程算法评价以解析方法进行性能评价

算法复杂性

1. 算法复杂性是算法运行所需要的计算机资源的量，需要时间资源的量称为时间复杂性，需要的空间资源的量称为空间复杂性
2. 算法复杂性只依赖于算法要解的问题的规模、算法的输入和算法本身的函数

问题和问题实例

1. 问题实例是问题的一个具体输入
2. 实例长度：表示实例的数据结构的长度
3. 实例特征：描述问题实例长度的参数，为了简化分析，我们往往用实例特征表示实例长度。比如n个元素的数组，可以用n来表示数组的规模，而忽略每个元素实际所占的字节
4. 例特征的选取有随意性，但要能客观地反应问题的规模
5. 算法分析建立算法执行时间或空间占用与实例特征的函数关系

空间复杂度

1. 程序p的空间复杂度指程序运行时所需的内存空间大小和实例特征的函数关系，记为$S_p(n)$，或者$S(n)$
2. 程序p的空间需求量包括两部分：$S(p)=c+S_p(n)$，c为常量(实例无关部分)，分析空间复杂度时我们忽略与实例特征无关的空间需求量，仅考虑$S_p(n)$
3. 程序运行时所需空间包括：
   1. 指令空间-与实例特征无关的常数❌
   2. 数据空间：
      1. 常量和简单变量-实例无关❌
      2. 复合变量(数组、链表、树和图等)
      3. 环境栈空间(函数调用)-是否递归?
      复合变量所需空间常常和问题实例特征有关
4. 从程序调用的角度看,存放无序表的数组占用的空间记在上层程序的帐上，也就是说如果输入用指针传入一个数组，只考虑指针所占的与实例长度无关的空间，所以相应的空间复杂度为0
5. 对非递归算法分析与实例特征有关的数据结构的大小，对递归算法还要分析递归调用的深度和实例特征的关系
   eg.

T sum(T a[], int n)
{
	T tsum = 0;
	for(int i=0;i<n;i++) tsum+=a[i];
	return tsum;
}

空间复杂度分析：实例特征为n，上述代码输入指针a，整型n，函数中的变量tsum，i，全都是与实例特征无关的常量和简单变量，所以空间复杂度$S(n)=0$

T rsum(T a[], int n)
{
	if(n>0) return rsum(a,n-1)+a[n-1];
	return 0;
}

空间复杂度分析：实例特征为n，每层递归有整型返回值，指针a，整型n，递归栈占6 bytes，从rsum(a,n)到rsum(a,0)，$S(n)=6(n+1)bytes$

时间复杂度

1. 时间复杂度指程序执行时所用的时间，程序p的时间复杂度表示为输入量的函数T，也就是$T(n)$

2. 两种时间单位

   1. 操作计数(operation count):算法的基本操作
   2. (程序)步计数(step count):分析全部程序，一条或多条执行时间是常数的语句称为“1步”，例如简单赋值语句；不涉及函数调用的表达式求值；简单的条件判断等。划分程序步的方法不唯一，t(n)也不唯一,但数量级唯一

   基本操作或程序步的执行时间必须是常数，要注意单行代码有没有调用函数。
   eg.

void rank(t a[],int n,int r[])
{
	for(int i=0;i<n;i++) r[i]=0; //1
	for(int i=1;i<n;i++) //2
	{
		for(int j=0;j<i;j++) //3
		{
			if(a[j]<=a[i]) r[i]++; //4
			else r[j]++; //4
		}
	}
}

根据操作计数，1的时间为n-1，2和3两重循环的时间是$1+2+...+n-1=\frac{n\ast (n-1)}{2}$，4的时间是常数，所以$t(n)=\frac{n\ast (n-1)}{2}$
这个程序可以求出每个元素是数组中第几大的元素

最好，最坏和平均情形时间复杂度

最好：1次成功
最坏：不成功
平均：求和每种情况所需的时间$\times$每种情况的概率

程序步计数和程序步表

对于递归程序，可以使用解递归方程

T rsum(T a[], int n)
{
	if(n>0) return rsum(a,n-1)+a[n-1];
	return 0;
}

t(0)=2并且t(n)=2t(n-1)+2，解得t(n)=2(n+1)，2就是比较和return两步

2. 注意这里b[j]=Sum(a,j+1)调用了图片1里的Sum函数，Sum函数的步数为2n+3，所以这里的步数为2(j+1)+3=2j+6 ，而这一语句会循环n次，所以总步数为$6n+{\sum }_{j=0}^{n-1}2j=6n+n(n-1)=n(n+5)$
   

4. 顺序查找最好情况

5.顺序查找最坏情况

渐进分析

1. O 上界
   1. $f(n)=O(g(n))$ 当且仅当存在常数$c$和$n_0$使得对所有$n>n_0$ 有$f(n)<cg(n)$ 成立，称g(n)为f(n)的渐近上界(Asymptotic Upper Bound)
   2. ${\lim }_{n->\infty }|\frac{f(n)}{g(n)}|=c$且 $0\le c<\infty$，则$f(n)=O(g(n))$
   3. 约定O(1)代表常数
   4. g(n)常取一些简单的初等函数,$n^k$,$lo{g}_{2}n$和$n^{k}lo{g}_{2}n$等
2. Ω 下界
   1. $f(n)=\Omega (g(n))$ 当且仅当存在常数$c$和$n_0$使得对所有$n>n_0$,有$f(n)>cg(n)$成立，称g(n)为f(n)的渐近下界
   2. ${\lim }_{n->\infty }|\frac{f(n)}{g(n)}|=c$且 $0<c\le \infty$，则$f(n)=\Omega (g(n))$
3. Θ
   1. 如果$f(n)=O(g(n))$同时 $f(n)=\Omega (g(n))$则$f(n)=\Theta (g(n))$,并称f(n)与g(n)同阶
   2. ${\lim }_{n->\infty }|\frac{f(n)}{g(n)}|=c$且 $0<c<\infty$，则$f(n)=\Theta (g(n))$

当f(n)为算法的时间复杂度函数时，称g(n)为该算法的复杂度的阶

常用渐进分析等式

$n!$~$(2\pi {)}^{\frac{1}{2}}{n}^{n+\frac{1}{2}}{e}^{-n}$

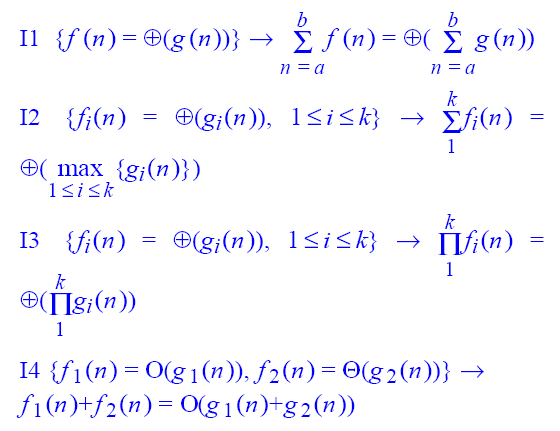
渐进分析例题

多项式时间算法

1. 如果一算法的最坏情形时间复杂度$t(n)=O(n^k)$,则称该算法为多项式复杂度的算法或有多项式界的算法.
2. 如果一算法的最坏情形时间复杂度t(n)不能用多项式限界,则称该算法为指数复杂度的算法。这类算法可认为计算上不可行的算法
3. 如果一个问题有多项式界的算法称该问题属于多项式类问题

算法概述中的问题举例

插入排序

最优二叉树

To do