分治法的应用--平面点对最小距离问题

问题描述：一个二维平面内有一些随机分布的点，求这些点之间距离最短的两个点。（问题和图片均出自于北京大学网课）

看到这个问题首先想到的应该是暴力解法，即对于每个点，遍历其他所有点求距离。把平面中任意两点的距离都求出来后，取其中的最小值。但是这个算法的时间复杂度为O(n^2)，当数据量较大时是无法接受的。

于是我们想到了分治法，可不可以将问题化简为求几个规模减小的子问题呢，答案是可以的，我们可以根据平面中的点的x坐标或y坐标将它们分为数目大致相等的两部分。这里我们以x坐标举例，如图：

我们可以在分治之前先将所有的点按x坐标从小到大排序，排序操作复杂度为O(nlogn)，这样只需取数组的中点的x坐标即可将点大致均分为两部分，分割操作复杂度为O(1)，将平面分割成两部分S1和S2后，平面中距离最短的两个点的分布有三种情况，两个点都在S1中、两个点都在S2中、两个点一个在S1中一个在S2中。

现在的问题是对于第三种情况，我们该如何求解？采用暴力法（求出S1中的每个点，到S2中所有）？当然不是，这样的话时间复杂度不会变化。

我们可以先求出S1中两点的最短距离d1，和S2中两点的最短距离d2，令d = min(d1, d2)，则可得若存在两个点p1、p2的距离小于d，那么它们一定分别属于S1和S2。且p1和p2距离分割线一定不超过d，如果两者之间有一个距离分割线超过d则p1和p2的距离一定会大于d。于是我们可以在分割线两边划分出一个中间区域，如下图：

 只需检查S1和S2落在中间区域的点的距离就可以了，但有一种极端情概况，即S1和S2的所有点都落在中间区域，为了避免这样的情况，我们可以继续对每个点扫描的区域加以限制，即p1和p2的Y轴坐标距离也不能超过d，这样两个点的距离才可能小于d。这样对于每个处在中间区域且属于S1的点p1，可以在S2中划出一块宽为d高为2d的长方形，若在S2中存在这样的p2使得p1、p2的距离小于d，则p2必定存在于这块区域中，如下图：

 

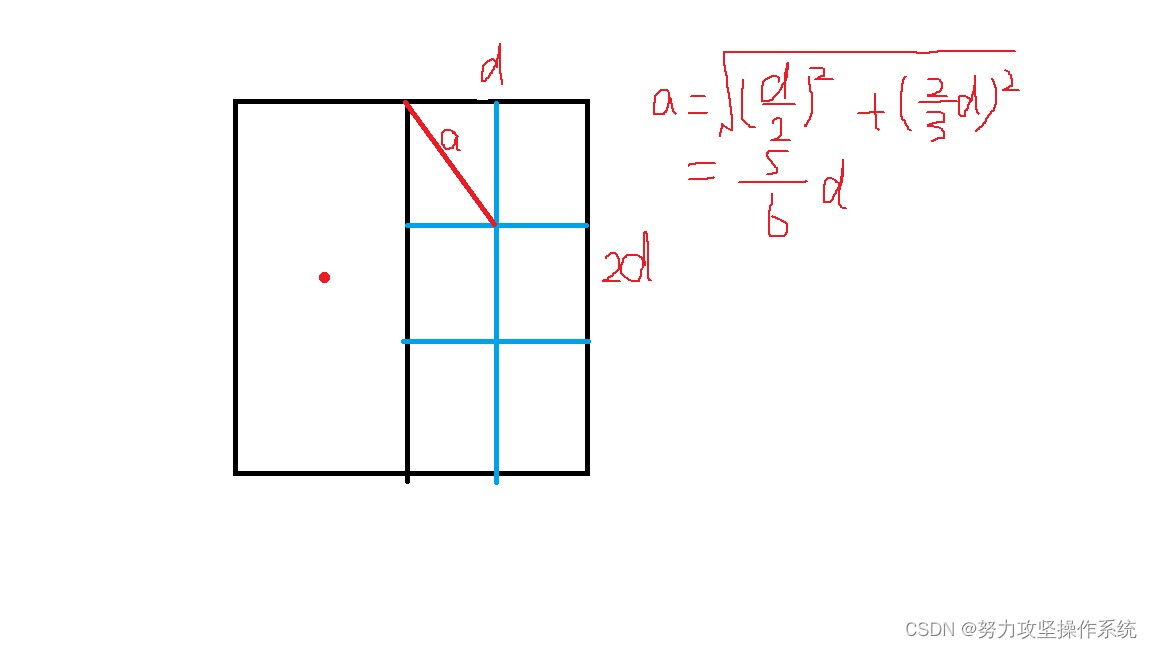
可知每个方格中至多存在一个点（因为S2中任意两点的距离大于d），即对于中间区域中的点，只需计算常数个点与它的距离即可，时间复杂度是线性的，那么如何能找到与任一点y轴坐标相差在d之内的点呢，我们可以将点按y轴坐标排序，但是该排序不能在分治的时候排序，因为排序的时间复杂度为O(nlogn)，若在每次分治合并处理是加上排序，则总的时间复杂度为O(nlognlogn)，此时我们有两种方案：

1、预处理，在分治开始之前对所有点按y坐标进行排序，每次分治时，扫描一遍该排好序的数组，将所有点按划分区域分为两部分，这样在每个区域，y坐标还是按序排好的，该操作的时间复杂度为O(n)

2、由于分治时划分点的方法与归并排序划分点的方法相同，我们可以一边分治一边归并排序，这样每次对点进行归并的时间复杂度也为O(n)

用以上两种方法实现的算法的时间复杂度为O(nlogn)

算法的结束条件：可以视情况而定，可以当点的个数小于等于5时就用暴力法计算出这5个点的最短距离并返回，也可以当点的个数小于等于2时算出最短距离并返回（注意：当有一边只有一个点时，返回值无穷大，因为只有一个点意味着没有最短距离，所以不能作为参考）

下面的代码我是用的归并排序： 

#include <iostream>
#include <cmath>
#include <deque>
#include <algorithm>
using namespace std;

struct point {
	int x;
	int y;
public:
	bool operator<(const point& a) {//按x坐标比较大小
		return x < a.x;
	}
};


//参数px是按x坐标排好序的点数组，start和end表示返回px中下标范围[start, end]中距离最小的两个点的距离
//py是px中下标范围[start, end]中的点按y坐标排序的结果，供归并排序使用
//对于该函数来说，px, start, end为输入参数，py为输出参数
double get_min_distance(point* px, int start, int end, point* py) {
	if (start == end) {//若范围内只有一个点，则返回无穷大
		py[0] = px[start];
		return DBL_MAX;
	}
	if (start == end - 1) {//若范围中有两个点，这两个点的距离即为最小距离
		py[0] = px[start].y > px[end].y ? px[end] : px[start];
		py[1] = px[start].y > px[end].y ? px[start] : px[end];
		return sqrt((px[start].x - px[end].x) * (px[start].x - px[end].x) + (px[start].y - px[end].y) * (px[start].y - px[end].y));
	}
	int mid = (start + end) / 2;
	int n1 = mid - start + 1;
	int n2 = end - mid;
	int n = end - start + 1;
	point* py1 = new point[n1];
	double d1 = get_min_distance(px, start, mid, py1);
	point* py2 = new point[n2];
	double d2 = get_min_distance(px, mid + 1, end, py2);
	double d = d1 > d2 ? d2 : d1;
	int i = 0, j = 0, k = 0;
	//下面是归并操作
	while (i < n1 && j < n2) {
		if (py1[i].y > py2[j].y)py[k++] = py2[j++];
		else py[k++] = py1[i++];
	}
	while (i < n1)py[k++] = py1[i++];
	while (j < n2)py[k++] = py2[j++];
	deque<point> qu;
	double dis = DBL_MAX;
	for (k = 0; k < n; k++) {
		if (py[k].x > px[mid].x - d && py[k].x < px[mid].x + d) {//注意在这一步操作中我没有将中间区域的点分为左边或右边讨论，这样不影响结果的正确性，且代码逻辑要简单不少，性能有常数级的下降
			while (!qu.empty() && py[k].y - qu.front().y >= d)qu.pop_front();
			if (!qu.empty()) {
				for (auto it = qu.begin(); it != qu.end(); ++it) {
					double r = sqrt((py[k].x - it->x) * (py[k].x - it->x) + (py[k].y - it->y) * (py[k].y - it->y));
					if (r < dis)dis = r;
				}
			}
			qu.push_back(py[k]);
		}
	}
	delete[] py1;
	delete[] py2;
	return d > dis ? dis : d;
}

int main() {
	cout << "请输入平面中点的数量：";
	int nums;
	cin >> nums;
	cout << "请按 x y 格式输入每个点的坐标,坐标之间用回车分隔：\n";
	point* px = new point[nums];
	for (int i = 0; i < nums; i++) {
		cin >> px[i].x >> px[i].y;
	}
	sort(px, px + nums);//将px数组按x坐标从小到大排序
	point* py = new point[nums];//创建py数组用于存放按y坐标从小到大排序的点
	cout << "最短距离为：" << get_min_distance(px, 0, nums - 1, py);
	delete[] py;
	return 0;
}