运筹优化-车辆路径优化-基础概念

在本科毕设中，常常需要写车辆路径优化问题，我正在小红书更新比较体系的讲解，方便读者用于迅速投入到学习/研究当中。

小红书：72 【运筹优化--车辆路径优化 - Akise Aru | 小红书 - 你的生活指南】 😆 INsW1a1PNYuuLRB 😆 https://www.xiaohongshu.com/discovery/item/675ea5ba000000000603f05b?source=webshare&xhsshare=pc_web&xsec_token=ABsE8SQe6Z3xCFhC6zXOVlpK5jReKFiA9VVdNg8OL52B0=&xsec_source=pc_share

考虑到小红书的内容似乎不被搜索引擎直接搜到，这里把我在小红书的博文搬到这里来。

在打数学建模比赛的时候，需要提前意识到一些基本概念：

数学模型：

简单来说，这是对现实问题/比赛问题的抽象表达，用数学语言表示；比如微分方程、线性规划、马尔科夫链等等。

求解算法：

有了数学模型，可以找出不同的算法来求解模型。因此严格来说，两者在比赛中是可以分为两个人的任务，后者往往比前者难（因为学生中会写程序的相对少；也因为如果模型搞错了，算法也会出问题）。

下面是ai的回答（比较详细、学术）

---

1. 数学模型的关键要素

1. 研究对象（问题背景）

   • 首先要明确要解决的实际问题是什么，比如交通优化、资源分配、生态平衡、疫情预测、金融风险测度等。
   • 要对问题进行具体描述，并收集相关数据和信息。

2. 模型假设

   • 在建立模型时，为简化或聚焦问题，通常会做出一些合理的假设。
   • 假设的选择需要兼顾真实情况与模型的可操作性，如忽略次要因素、简化某些复杂关系等。

3. 变量选取和参数设定

   • 根据问题背景，需要定义哪些量是需要关注的（自变量、因变量、状态变量、控制变量等）。
   • 还要确认模型中需要哪些参数，参数反映系统固有的特性或外部环境对系统的影响。

4. 数学关系式或函数

   • 将问题中的因果关系、约束条件等用数学方程或不等式等形式表达出来。
   • 常见的表达方式包括：线性或非线性方程组、微分方程组、概率统计模型等。

5. 求解方法

   • 确定用什么方法来求解模型：解析法（手推公式）、数值方法、算法（如线性规划、动态规划、模拟退火等）。
   • 在建模比赛中，往往会结合实际数据进行仿真、迭代、优化等。

6. 结果分析与检验

   • 求出结果后，需要对模型结果的有效性与合理性进行分析。
   • 可以进行灵敏度分析或用真实数据进行检验，不断修正或改进模型。

---

2. 常见类型的数学模型

1. 线性规划模型

   • 用于处理线性目标函数与线性约束的一类模型，比如资源分配、生产优化等。
   • 常见的求解工具：单纯形法、内点法等。

2. 回归模型

   • 针对大规模数据，通过回归分析找到自变量与因变量之间的统计关系。
   • 常见的有线性回归、逻辑回归、多元回归、非线性回归等。

3. 时间序列预测模型

   • 针对具有时间关联的数据（如股票价格、销量等）进行预测。
   • 常见的模型包括ARIMA、指数平滑、LSTM（深度学习）等。

4. 微分方程模型

   • 对动态系统进行刻画，如人口增长、传染病传播、物理运动等。
   • 常见形式包括常微分方程（ODE）、偏微分方程（PDE）。

5. 马尔可夫链与排队论

   • 用于处理随机过程相关问题，如客户排队、系统可靠性、转移概率等。

6. 博弈论模型

   • 分析多个参与方相互影响与决策的情况，如市场竞争、谈判策略等。

7. 网络与图论模型

   • 用于描述网络结构（如社交网络、交通网络、物流网络）以及在网络上进行的优化，比如最短路径、最大流-最小割等。

8. 机器学习/深度学习模型

   • 面对海量、高维数据时，可以借助机器学习算法（如SVM、随机森林、神经网络等）寻找更复杂的模式和规律。

---

以上是ai的回答

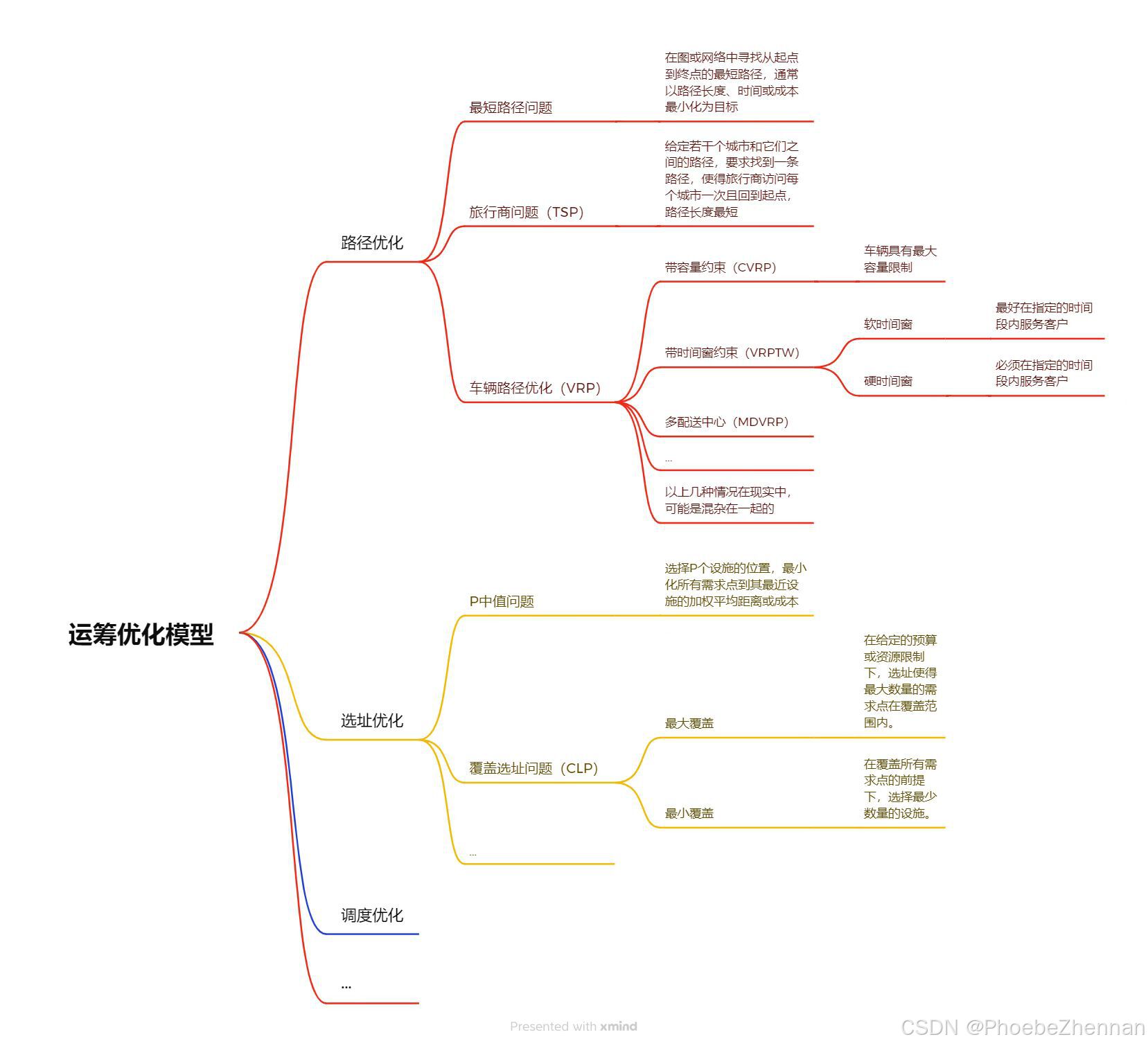
运筹优化模型

其中，运筹优化模型，属于数学模型中的一类：

        我关注的车辆路径优化，又属于运筹优化模型中的一类

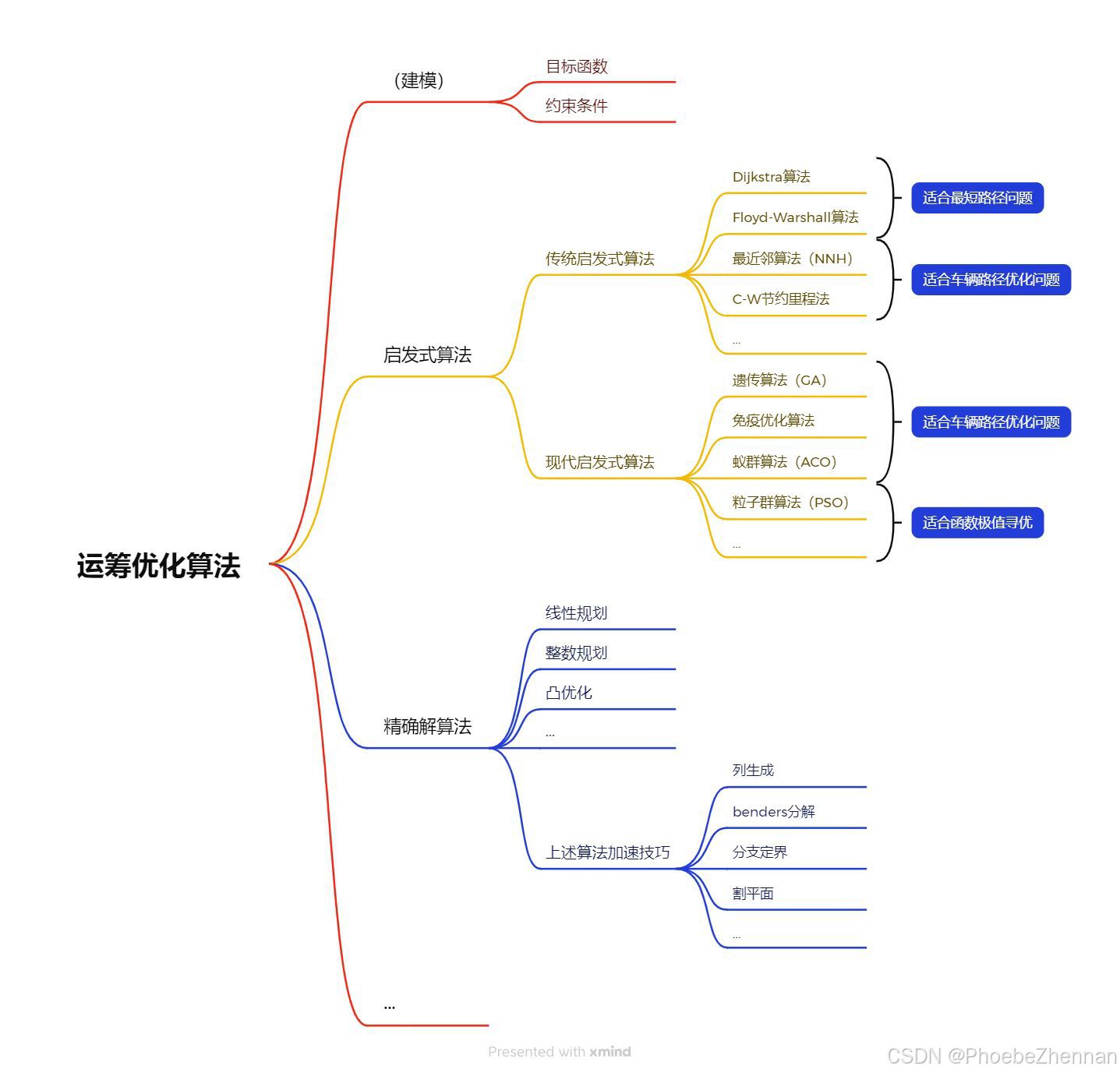
运筹优化算法

运筹优化算法，是解决运筹优化模型时，常用的一些算法。两者很多时候是多对多的关系：一种模型可以用多种算法求解，一种算法也可以通过改造来求解多种模型。

        我本科比较关注的是启发式算法，因为当时觉得遗传算法听上去很高端呵呵呵。