【手撕系列】手撕Llama3

---

本系列旨在记录整理本人学习的过程和思考，因水平有限，可能理解的不够深入，欢迎指出问题和探讨交流。部分素材参考网上其他教程，在本文最后列出参考链接。
本文代码放在：https://github.com/WKQ9411/mini-llama3-from-scratch，如果对您有所帮助，欢迎star！

概览

Llama3的整体结构如下图：
Llama 3 使用标准的密集 Transformer 解码器架构。在模型架构方面，它与 Llama 和 Llama 2 没有明显差异，性能提升主要得益于数据质量和多样性的提高，以及训练规模的增加。

本文主要介绍以下改进的地方：

• RMSNorm归一化
• 旋转位置编码RoPE
• 分组查询注意力机制GQA和KV Cache
• FFN和SwiGLU激活函数

一、RMSNorm归一化

（一）基本概念

回顾一下 Batch Norm 和 Layer Norm 的区别：

引自：一图概括BatchNorm与LayerNorm的关系

• BatchNorm是对整个 batch 样本内的每个特征做归一化，这消除了不同特征之间的大小关系，但是保留了不同样本间的大小关系。
• LayerNorm是对每个样本的所有特征做归一化，这消除了不同样本间的大小关系，但是保留了一个样本内不同特征之间的大小关系。

RMSNorm的提出是为了解决LayerNorm在训练大型模型时计算开销较大的问题。 RMSNorm与LayerNorm的主要区别在于不需要计算均值。它通过以下公式实现归一化：

$$\text{RMSNorm}(x)=\frac{x}{\text{RMS}(x)}\odot \gamma$$

其中：

$$\text{RMS}(x)=\sqrt{\frac{1}{d}\sum _{i=1}^d{x}_i^2+ϵ}$$

（二）代码

实现代码如下：

# RMS归一化
class RMSNorm(torch.nn.Module):
    def __init__(self, dim: int, eps: float = 1e-6):
        super().__init__()
        self.eps = eps
        self.weight = nn.Parameter(torch.ones(dim))

    def _norm(self, x):
        # 输入维度为(batch_size, seq_len, emb),对最后一个维度进行归一化
        # x.pow(2)用于对每个元素进行平方运算
        # torch.rsqrt()是计算倒数平方根
        return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)

    def forward(self, x):
        output = self._norm(x.float()).type_as(x)
        return output * self.weight

二、旋转位置编码RoPE

外推能力是指位置编码能否帮助模型处理超出训练范围的序列长度或位置索引的能力。当模型在训练时只见过特定长度的序列，或者在特定的范围内学习了位置相关的特征（如$[1,100]$），如果在推理时遇到更长的序列（例如长度为200），模型是否仍然能够正确地处理序列中的位置信息，就体现了位置编码的外推能力。

位置编码主要有两种类型：绝对位置编码 和 相对位置编码。

• 学习型绝对位置编码（Learnable Absolute Positional Encoding）通过参数化直接学习每个位置的嵌入向量。只能处理训练时见过的序列长度，无法外推到未见位置，因为超出范围的位置没有定义的编码。
• 正弦-余弦位置编码（Sinusoidal Positional Encoding） 是绝对位置编码，理论上也具有一定的外推能力，但 对过长序列的效果有限。
• 相对位置编码（Relative Positional Encoding）相对位置编码基于位置差值来表示位置关系，而不是绝对位置。天然具有外推能力，因为相对差值的计算方式不会依赖具体的序列长度。
• 混合型位置编码（例如 Rotary Position Embedding, RoPE）RoPE位置编码通过将一个向量旋转某个角度，为其赋予位置信息。通过绝对位置编码的方式实现相对位置编码。

位置编码的外推参考：深度探讨大模型位置编码及其外推性

（一）基本概念

令 S N = { w i } i = 1 N \mathbb{S}_N=\{w_i\}_{i=1}^N SN​={wi​}i=1N​为一个具有$N$个tokens的输入序列，$w_i$为第$i$个位置的token。

令 E N = { x i } i = 1 N \mathbb{E}_N=\{\boldsymbol{x}_i\}_{i=1}^N EN​={xi​}i=1N​是该序列对应的embedding，${\mathbf{x}}_i\in {\mathbb{R}}^d$是$w_i$的没有加入位置信息的词嵌入。

自注意力机制 首先将位置信息融入到词嵌入中，然后将其转化为查询(Q)、键(K)和值(V)表示，可以表示为：

$$\begin{array}{rl}{\mathbf{q}}_m& =f_q({\mathbf{x}}_m,m)\\ {\mathbf{k}}_n& =f_k({\mathbf{x}}_n,n)\\ {\mathbf{v}}_n& =f_v({\mathbf{x}}_n,n)\end{array}\text{\hspace{1em}(1)}$$
其中 ${\mathbf{q}}_m$、${\mathbf{k}}_n$ 和 ${\mathbf{v}}_n$ 分别表示通过 $f_q$、$f_k$、$f_v$ 加入了第 $m^{th}$ 和第 $n^{th}$ 个 位置信息，并经过 线性变换 得到的查询(Q)、键(K)和值(V)。

由Q与K计算得到注意力分数：

$$a_{m,n}=\frac{\exp (\frac{{\mathbf{q}}_m^{⊺}{\mathbf{k}}_n}{\sqrt{d}})}{{\sum }_{j=1}^N\exp (\frac{{\mathbf{q}}_m^{⊺}{\mathbf{k}}_j}{\sqrt{d}})}\text{\hspace{1em}(2)}$$

并对V进行加权求和得到$m^{th}$位置的最终输出：

$${\mathbf{o}}_m=\sum _{n=1}^N{a}_{m,n}{\mathbf{\upsilon }}_n$$

以下绝对位置编码和相对位置编码的内容源于RoPE原文的“背景及相关工作”部分，可以仅作为了解。

绝对位置编码

上述公式（1）中函数 $f$ 的典型形式是：

f t : t ∈ { q , k , v } ( x i , i ) : = W t : t ∈ { q , k , v } ( x i + p i ) (3) f_{t:t\in\{q,k,v\}}(\boldsymbol{x}_i,i):=\boldsymbol{W}_{t:t\in\{q,k,v\}}(\boldsymbol{x}_i+\boldsymbol{p}_i) \tag{3} ft:t∈{q,k,v}​(xi​,i):=Wt:t∈{q,k,v}​(xi​+pi​)(3)

其中${\mathbf{p}}_i\in {\mathbb{R}}^d$是位置信息。该公式的含义即：

1. 先给 $i$ 位置的嵌入加上位置信息
2. 再使用线性变换得到Q/K/V矩阵

在Transformer中，$p_i$即为 绝对位置编码：

$$\{\begin{array}{llc}{\mathbf{p}}_{i,2t}& =\sin (i/10000^{2t/d})& \\ {\mathbf{p}}_{i,2t+1}& =\cos (i/10000^{2t/d})& \end{array}$$

与这一绝对位置编码方法不同的是，RoPE提出通过将位置信息与正弦函数相乘来融入相对位置信息，而不是直接将位置信息加到上下文表示中。

原文叙述：instead of directly adding the position to the context representation, RoPE proposes to incorporate the relative position information by multiplying with the sinusoidal functions.

相对位置编码

Self-Attention with Relative Position Representations使用的不同形式的公式（1）：

$$\begin{array}{rl}{f}_q({\mathbf{x}}_m)& :={\mathbf{W}}_q{\mathbf{x}}_m\\ f_k({\mathbf{x}}_n,n)& :={\mathbf{W}}_k({\mathbf{x}}_n+{\tilde{\mathbf{p}}}_r^k)\\ f_v({\mathbf{x}}_n,n)& :={\mathbf{W}}_v({\mathbf{x}}_n+{\tilde{\mathbf{p}}}_r^v)\end{array}$$
其中 ${\tilde{\mathbf{p}}}_r^k,{\tilde{\mathbf{p}}}_r^v\in {\mathbb{R}}^d$ 是可训练的相对位置嵌入。$r=\mathrm{clip}(m-n,r_{\min },r_{\max })$ 表示位置 $m$ 和 $n$ 之间的相对距离，并通过“裁剪”（clip）操作将其限制在一个范围内（即 $r_{\text{min}}$ 和 $r_{\text{max}}$ 之间）。这样做的假设是，当两个位置之间的距离超过某个范围时，过于精确的相对位置信息对实际任务不再重要，甚至可能对结果产生负面影响。因此，通过裁剪将距离限制在一个合理的范围内，可以提高模型的效率并减少噪声的影响。

Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context将公式（3）形式的$f$代入到公式（2）中的${\mathbf{q}}_m^{⊺}{\mathbf{k}}_n$并展开有：

$$\begin{array}{rl}{\mathbf{q}}_m^{⊺}{\mathbf{k}}_n& =[{\mathbf{W}}_q({\mathbf{x}}_m+{\mathbf{p}}_m){]}^{⊺}[{\mathbf{W}}_k({\mathbf{x}}_n+{\mathbf{p}}_n)]\\ & =({\mathbf{x}}_m+{\mathbf{p}}_m{)}^{⊺}{\mathbf{W}}_q^{⊺}{\mathbf{W}}_k({\mathbf{x}}_n+{\mathbf{p}}_n)\\ & ={\mathbf{x}}_m^{⊺}{\mathbf{W}}_q^{⊺}{\mathbf{W}}_k{\mathbf{x}}_n+{\mathbf{x}}_m^{⊺}{\mathbf{W}}_q^{⊺}{\mathbf{W}}_k{\mathbf{p}}_n+{\mathbf{p}}_m^{⊺}{\mathbf{W}}_q^{⊺}{\mathbf{W}}_k{\mathbf{x}}_n+{\mathbf{p}}_m^{⊺}{\mathbf{W}}_q^{⊺}{\mathbf{W}}_k{\mathbf{p}}_n\end{array}$$

其核心思想是使用相对位置表征 ${\tilde{\mathbf{p}}}_{m-n}$ 替换绝对位置表征 ${\mathbf{p}}_n$ ；第三第四项中的绝对位置表征 ${\mathbf{p}}_m$ 分别替换为可学习向量 $\mathbf{u}$ 和 $\mathbf{v}$ ；${\mathbf{W}}_k$ 被区分基于内容 ${\mathbf{x}}_n$ 的和基于位置 ${\mathbf{p}}_n$ 的 ${\mathbf{W}}_k$ 和 ${\tilde{\mathbf{W}}}_k$，因此可进一步表示为：
$${\mathbf{q}}_m^{⊺}{\mathbf{k}}_n={\mathbf{x}}_m^{⊺}{\mathbf{W}}_q^{⊺}{\mathbf{W}}_k{\mathbf{x}}_n+{\mathbf{x}}_m^{⊺}{\mathbf{W}}_q^{⊺}{\tilde{\mathbf{W}}}_k{\tilde{\mathbf{p}}}_{m-n}+{\mathbf{u}}^{⊺}{\mathbf{W}}_q^{⊺}{\mathbf{W}}_k{\mathbf{x}}_n+{\mathbf{v}}^{⊺}{\mathbf{W}}_q^{⊺}{\tilde{\mathbf{W}}}_k{\tilde{\mathbf{p}}}_{m-n}$$

（二）RoPE

二维情形

二维情形源于原文3.2.1节，直接给出结论，证明在后面。

为了融入相对位置信息，我们要求查询${\mathbf{q}}_m$和键${\mathbf{k}}_n$的内积由一个函数$g$来描述，该函数 $g$ 仅以词向量 ${\mathbf{x}}_m$，${\mathbf{x}}_n$ 和它们的相对位置 $n-m$ 作为输入变量。即需要找到一个等价的编码机制来求解函数 $f_q({\mathbf{x}}_m,m)$ 和 $f_k({\mathbf{x}}_n,n)$，使其满足：

$${\mathbf{q}}_m^{⊺}{\mathbf{k}}_n=⟨f_q({\mathbf{x}}_m,m),f_k({\mathbf{x}}_n,n)⟩=g({\mathbf{x}}_m,{\mathbf{x}}_n,n-m)\text{\hspace{1em}(4)}$$

原文在介绍二维情形时用了$m-n$，在推导时用了$n-m$，为了保持一致，我这里全部使用$n-m$，复数计算时相当于对$f_q$取了共轭复数，详见后面的推导。

在2维情形下，公式（4）可通过复数形式推导求解【原文3.4.1证明】，它的一个 复数形式的解 是：

$$\begin{array}{rl}{f}_q({\mathbf{x}}_m,m)& =({\mathbf{W}}_q{\mathbf{x}}_m)e^{im\theta }\\ f_k({\mathbf{x}}_n,n)& =({\mathbf{W}}_k{\mathbf{x}}_n)e^{in\theta }\\ g({\mathbf{x}}_m,{\mathbf{x}}_n,m-n)& =\mathrm{Re}[({\mathbf{W}}_q{\mathbf{x}}_m{)}^{\ast }({\mathbf{W}}_k{\mathbf{x}}_n)e^{i(n-m)\theta }]\end{array}$$
其中，$\mathrm{Re}[\cdot ]$ 是取复数的实部，$({\mathbf{W}}_q{\mathbf{x}}_m{)}^{\ast }$ 是 $({\mathbf{W}}_q{\mathbf{x}}_m)$ 的共轭复数，$\theta \in \mathbb{R}$ 是 预设的非零常数。

复数的内积（共轭乘积）是通过将一个复数取共轭并与另一个复数相乘来定义的，即$⟨z_1,z_2⟩=z_1^{\ast }{z}_2$
标准形式：
假设有两个复数：$z_1=a_1+b_{1}i,z_2=a_2+b_{2}i$，$z_1$的共轭复数$z_1^{\ast }=a_1-b_{1}i$
内积的计算结果为：$⟨z_1,z_2⟩=(a_1{a}_2+b_1{b}_2)+(a_1{b}_2-b_1{a}_2)i$，因此其 结果的实部即就是二维向量的内积
极坐标形式：
在极坐标形式下，复数$z_1$和$z_2$表示为：$z_1=r_1{e}^{i{\theta }_1},z_2=r_2{e}^{i{\theta }_2}$，$z_1$的共轭复数$z_1^{\ast }=r_1{e}^{-i{\theta }_1}$
内积的计算结果为：$⟨z_1,z_2⟩=r_1{r}_2{e}^{i({\theta }_2-{\theta }_1)}$
因此上述 $\mathbf{x}$ 经过 $f$ 编码后，写为复数形式，取实部才是最终需要计算的attention。

🔥可以进一步将 f { q , k } f_{\{q,k\}} f{q,k}​写为矩阵乘法的形式：

f { q , k } ( x m , m ) = ( cos ⁡ m θ − sin ⁡ m θ sin ⁡ m θ cos ⁡ m θ ) ( W { q , k } ( 11 ) W { q , k } ( 12 ) W { q , k } ( 21 ) W { q , k } ( 22 ) ) ( x m ( 1 ) x m ( 2 ) ) f_{\{q,k\}}(\boldsymbol{x}_m,m)= \begin{pmatrix} \cos m\theta & -\sin m\theta \\ \sin m\theta & \cos m\theta \end{pmatrix} \begin{pmatrix} W_{\{q,k\}}^{(11)} & W_{\{q,k\}}^{(12)} \\ W_{\{q,k\}}^{(21)} & W_{\{q,k\}}^{(22)} \end{pmatrix} \begin{pmatrix} x_m^{(1)} \\ x_m^{(2)} \end{pmatrix} f{q,k}​(xm​,m)=(cosmθsinmθ​−sinmθcosmθ​)(W{q,k}(11)​W{q,k}(21)​​W{q,k}(12)​W{q,k}(22)​​)(xm(1)​xm(2)​​)

因此，融入相对位置信息很简单：只需将仿射变换后的词嵌入向量旋转一定角度，该角度是其位置索引的倍数，从而解释了旋转位置嵌入（Rotary Position Embedding）的直观含义。

多维情形

为了将2维情形推广到 ${\mathbf{x}}_i\in {\mathbb{R}}^d$ 的多维情形（其中 $d$ 为 偶数），可将 $d$ 维空间分成 $d/2$ 个子空间， f { q , k } f_{\{q,k\}} f{q,k}​ 转化为：

f { q , k } ( x m , m ) = R Θ , m d W { q , k } x m f_{\{q,k\}}(\boldsymbol{x}_m,m)=\boldsymbol{R}_{\Theta,m}^d\boldsymbol{W}_{\{q,k\}}\boldsymbol{x}_m f{q,k}​(xm​,m)=RΘ,md​W{q,k}​xm​

其中🔥
$${\mathbf{R}}_{\Theta ,m}^d=\left(\begin{array}{ccccccc}\cos m{\theta }_1& -\sin m{\theta }_1& 0& 0& \cdots & 0& 0\\ \sin m{\theta }_1& \cos m{\theta }_1& 0& 0& \cdots & 0& 0\\ 0& 0& \cos m{\theta }_2& -\sin m{\theta }_2& \cdots & 0& 0\\ 0& 0& \sin m{\theta }_2& \cos m{\theta }_2& \cdots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& 0& \cdots & \cos m{\theta }_{d/2}& -\sin m{\theta }_{d/2}\\ 0& 0& 0& 0& \cdots & \sin m{\theta }_{d/2}& \cos m{\theta }_{d/2}\end{array}\right)$$
是 带有预定义参数的旋转矩阵【该矩阵大小为(d,d)】，一个旋转矩阵是针对一个位置 $m$ 的向量而言的，用于为该位置的向量编码位置信息，即两两维度进行旋转，其中 Θ = { θ i = 1000 0 − 2 ( i − 1 ) / d , i ∈ [ 1 , 2 , . . . , d / 2 ] } \Theta=\{\theta_i=10000^{-2(i-1)/d},i\in[1,2,...,d/2]\} Θ={θi​=10000−2(i−1)/d,i∈[1,2,...,d/2]}，若 $i$ 从0开始，则为${\theta }_i=10000^{-2i/d}$。

代入到${\mathbf{q}}_m^{⊺}{\mathbf{k}}_n$的计算中有：

$${\mathbf{q}}_m^{⊺}{\mathbf{k}}_n=({\mathbf{R}}_{\Theta ,m}^d{\mathbf{W}}_q{\mathbf{x}}_m{)}^{⊺}({\mathbf{R}}_{\Theta ,n}^d{\mathbf{W}}_k{\mathbf{x}}_n)={\mathbf{x}}_m^{⊺}{\mathbf{W}}_q^{⊺}{\mathbf{R}}_{\Theta ,n-m}^d{\mathbf{W}}_k{\mathbf{x}}_n$$

其中 ${\mathbf{R}}_{\Theta ,n-m}^d=({\mathbf{R}}_{\Theta ,m}^d{)}^{⊺}{\mathbf{R}}_{\Theta ,n}^d$，因此这使得计算注意力时融入了相对位置信息。由于 ${\mathbf{R}}_{\Theta }^d$ 的 稀疏性，应用上面的矩阵乘法在计算效率上是不高的，因此原文提出更高效的实现，即将上式展开，按三角函数类型重新组合，得到下面更高效的计算方法🔥：

$${\mathbf{R}}_{\Theta ,m}^d\mathbf{x}=\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ ⋮\\ x_{d-1}\\ x_d\end{array}\right)\otimes \left(\begin{array}{c}\cos m{\theta }_1\\ \cos m{\theta }_1\\ \cos m{\theta }_2\\ \cos m{\theta }_2\\ ⋮\\ \cos m{\theta }_{d/2}\\ \cos m{\theta }_{d/2}\end{array}\right)+\left(\begin{array}{c}-x_2\\ x_1\\ -x_4\\ x_3\\ ⋮\\ -x_d\\ x_{d-1}\end{array}\right)\otimes \left(\begin{array}{c}\sin m{\theta }_1\\ \sin m{\theta }_1\\ \sin m{\theta }_2\\ \sin m{\theta }_2\\ ⋮\\ \sin m{\theta }_{d/2}\\ \sin m{\theta }_{d/2}\end{array}\right)$$
这里的 $\mathbf{x}$ 实际上是前文的 $\mathbf{W}\mathbf{x}$，这里是泛指。

综上，RoPE原理如下图：

二维复数形式推导

源于原文3.4.1节，针对二维时的推导

如前文所述，需要找到一个等价的编码机制来求解函数 $f_q({\mathbf{x}}_m,m)$ 和 $f_k({\mathbf{x}}_n,n)$，使其满足：

$${\mathbf{q}}_m^{⊺}{\mathbf{k}}_n=⟨f_q({\mathbf{x}}_m,m),f_k({\mathbf{x}}_n,n)⟩=g({\mathbf{x}}_m,{\mathbf{x}}_n,n-m)\text{\hspace{1em}(5)}$$

为了简化问题，首先假设词向量是二维的，即 $d=2$，设置以下初始化条件，它表示对带有 空位置信息 时的向量进行编码：

$$\begin{gathered} \mathbf{q}=f_q({\mathbf{x}}_q,0), \\ \mathbf{k}=f_k({\mathbf{x}}_k,0), \end{gathered}$$
对于2维向量，可以用平面几何和复数来表示，因此有如下 复数形式 的表示：
$$\begin{array}{rl}{f}_q({\mathbf{x}}_q,m)& =R_q({\mathbf{x}}_q,m)e^{i{\Theta }_q({\mathbf{x}}_q,m)},\\ f_k({\mathbf{x}}_k,n)& =R_k({\mathbf{x}}_k,n)e^{i{\Theta }_k({\mathbf{x}}_k,n)},\\ g({\mathbf{x}}_q,{\mathbf{x}}_k,n-m)& =R_g({\mathbf{x}}_q,{\mathbf{x}}_k,n-m)e^{i{\Theta }_g({\mathbf{x}}_q,{\mathbf{x}}_k,n-m)}\end{array}$$
其中，$R_f$、$R_g$ 和 ${\Theta }_f$、${\Theta }_g$ 分别表示 f { q , k } f_{\{q,k\}} f{q,k}​ 和 $g$ 的 径向和角度分量。将其带入公式（5），得到如下关系，这里在计算时对 $f_q$ 取了共轭复数：
$$\begin{array}{rl}{R}_q({\mathbf{x}}_q,m)R_k({\mathbf{x}}_k,n)& =R_g({\mathbf{x}}_q,{\mathbf{x}}_k,n-m),\\ {\Theta }_k({\mathbf{x}}_k,n)-{\Theta }_q({\mathbf{x}}_q,m)& ={\Theta }_g({\mathbf{x}}_q,{\mathbf{x}}_k,n-m),\end{array}$$
因此上式初始化条件为：
$$\begin{gathered} \mathbf{q}=\Vert \mathbf{q}\Vert e^{i{\theta }_q}=R_q({\mathbf{x}}_q,0)e^{i{\Theta }_q({\mathbf{x}}_q,0)}, \\ \mathbf{k}=\Vert \mathbf{k}\Vert e^{i{\theta }_k}=R_k({\mathbf{x}}_k,0)e^{i{\Theta }_k({\mathbf{x}}_k,0)}, \end{gathered}$$
其中，$\Vert \mathbf{q}\Vert$、$\Vert \mathbf{k}\Vert$ 和 ${\theta }_q$、${\theta }_k$ 分别是 $\mathbf{q}$、$\mathbf{k}$ 在2维平面上的径向和角度。

接下来，同时考虑 $m=n$ 和初始化条件，就有：

$$\begin{gathered} R_q({\mathbf{x}}_q,m)R_k({\mathbf{x}}_k,m)=R_g({\mathbf{x}}_q,{\mathbf{x}}_k,0)=R_q({\mathbf{x}}_q,0)R_k({\mathbf{x}}_k,0)=\Vert \mathbf{q}\Vert \Vert \mathbf{k}\Vert ,(6a) \\ {\Theta }_k({\mathbf{x}}_k,m)-{\Theta }_q({\mathbf{x}}_q,m)={\Theta }_g({\mathbf{x}}_q,{\mathbf{x}}_k,0)={\Theta }_k({\mathbf{x}}_k,0)-{\Theta }_q({\mathbf{x}}_q,0)={\theta }_k-{\theta }_q.(6b) \end{gathered}$$
对于公式（6a），$m$ 可以是任意值，他们最终都等于 $\Vert \mathbf{q}\Vert \Vert \mathbf{k}\Vert$，因此形式上可以写为：
$$R_q({\mathbf{x}}_q,m)R_k({\mathbf{x}}_k,m)=R_q({\mathbf{x}}_q,n)R_k({\mathbf{x}}_k,n)=\Vert \mathbf{q}\Vert \Vert \mathbf{k}\Vert$$
因此可得到一组直观的解：
$$\begin{array}{c}{R}_q({\mathbf{x}}_q,m)=R_q({\mathbf{x}}_q,0)=\Vert \mathbf{q}\Vert \\ R_k({\mathbf{x}}_k,n)=R_k({\mathbf{x}}_k,0)=\Vert \mathbf{k}\Vert \\ R_g({\mathbf{x}}_q,{\mathbf{x}}_k,n-m)=R_g({\mathbf{x}}_q,{\mathbf{x}}_k,0)=\Vert \mathbf{q}\Vert \Vert \mathbf{k}\Vert \end{array}$$
这表明 $R_q$、$R_k$、$R_g$ 独立于位置信息。

对于公式（6b），有 ${\Theta }_q({\mathbf{x}}_q,m)-{\theta }_q={\Theta }_k({\mathbf{x}}_k,m)-{\theta }_k$，我们设 ${\Theta }_f:={\Theta }_q={\Theta }_k$，即角度函数具有相同的形式，这就表明它们在经过位置编码后，对应的增量角度是相等的，即 ${\Theta }_q({\mathbf{x}}_q,m)$ 相比query的初始角度 ${\theta }_q$ 和 ${\Theta }_k({\mathbf{x}}_k,m)$ 相比key的初始角度 ${\theta }_k$ 的增加量是一样的，因而角度变化不依赖于它们各自的具体内容，而仅仅依赖于它们在序列中的位置。

即有仅与位置相关的函数 $\varphi (m)$：

ϕ ( m ) = Θ f ( x { q , k } , m ) − θ { q , k } \phi(m)=\Theta_f(\boldsymbol{x}_{\{q,k\}},m)-\theta_{\{q,k\}} ϕ(m)=Θf​(x{q,k}​,m)−θ{q,k}​

它的含义是：不论对query ${\mathbf{x}}_q$ 还是key ${\mathbf{x}}_k$，对同样的 $m$，他们编码后的角度增量都相同。

取 $n=m+1$，对于公式（6b）有：

$${\Theta }_k({\mathbf{x}}_k,m+1)-{\Theta }_q({\mathbf{x}}_q,m)={\Theta }_g({\mathbf{x}}_q,{\mathbf{x}}_k,1)$$

对于函数 $\varphi$ 有：

$$\begin{gathered} \varphi (m+1)={\Theta }_k({\mathbf{x}}_k,m+1)-{\theta }_k \\ \varphi (m)={\Theta }_q({\mathbf{x}}_q,m)-{\theta }_q \end{gathered}$$
因此得到：$\varphi (m+1)-\varphi (m)={\Theta }_g({\mathbf{x}}_q,{\mathbf{x}}_k,1)+{\theta }_q-{\theta }_k$ 上述等式右边是一个恒定值，可见函数 $\varphi$ 取整数位置时是一个等差序列，因而可以写为：$\varphi (m)=m\theta +\gamma$ 其中 $\theta ,\gamma \in \mathbb{R}$ 且 $\theta$ 不为0。

总结上述公式，得到：

$$\begin{gathered} f_q({\mathbf{x}}_q,m)=\Vert \mathbf{q}\Vert e^{i{\theta }_q+m\theta +\gamma }=\mathbf{q}{e}^{i(m\theta +\gamma )}, \\ {f}_k({\mathbf{x}}_k,n)=\Vert \mathbf{k}\Vert e^{i{\theta }_k+n\theta +\gamma }=\mathbf{k}{e}^{i(n\theta +\gamma )}. \end{gathered}$$
我们不对 $\mathbf{q}=f_q({\mathbf{x}}_q,0),\mathbf{k}=f_k({\mathbf{x}}_k,0),$ 加任何约束，因此可以定义为：$$\begin{gathered} \mathbf{q}=f_q({\mathbf{x}}_m,0)={\mathbf{W}}_q{\mathbf{x}}_n, \\ \mathbf{k}=f_k({\mathbf{x}}_n,0)={\mathbf{W}}_k{\mathbf{x}}_n. \end{gathered}$$
这种形式与Transformer中的线性变换一致。此外，设置 $\gamma =0$，因此有 $f_q$，$f_k$形式如下🔥：

$$\begin{gathered} f_q({\mathbf{x}}_m,m)=({\mathbf{W}}_q{\mathbf{x}}_m)e^{im\theta }, \\ {f}_k({\mathbf{x}}_n,n)=({\mathbf{W}}_k{\mathbf{x}}_n)e^{in\theta }. \end{gathered}$$

即就是简单的为query和key旋转一个角度，便能使其在计算attention时获取相对位置信息。

（三）代码

# 预先计算旋转矩阵的各个角度
def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
    """计算频率矩阵, 并将其表示为复数的极坐标表示, 函数名中的cis指cos(θ)+i·sin(θ), 表示一个复数位于单位圆上的位置

    Args:
        dim (int): Embedding的维度
        end (int): 序列长度
        theta (float, optional): 计算θ的底数值【θ=10000^(-2i/d)】. Defaults to 10000.0.

    Returns:
        代表各个位置m旋转角度的复数矩阵, 形状为(end, dim//2), 每两个维度对应一个旋转角度
    """
    # 计算旋转矩阵中的θ值, 原文中θ=10000^(-2i/d)【这里源代码[: (dim // 2)]的操作似乎是冗余的？】
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))

    # 计算位置信息m的序列
    t = torch.arange(end, device=freqs.device, dtype=torch.float32)

    # torch.outer用于计算外积, 就得到不同位置m和不同θ值的所有组合m*θ
    # 得到的freqs矩阵形状为(end, dim//2), 索引含义为freqs[mi][θi]=mi*θi
    freqs = torch.outer(t, freqs)

    # 生成一个模长为1, 幅角为freqs的复数矩阵
    freqs_cis = torch.polar(torch.ones_like(freqs), freqs)  # complex64
    return freqs_cis


# 调整freqs_cis以方便其与x进行广播计算
def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):
    """调整freqs_cis以方便其与x进行广播计算

    Args:
        freqs_cis (torch.Tensor): 旋转矩阵, 初始形状为(end, head_dim//2)
        x (torch.Tensor): query, 初始形状为(batch_size, seq_len, n_heads, head_dim//2)

    Returns:
        调整形状后的旋转矩阵, 形状为(1, seq_len, 1, head_dim//2)
    """
    ndim = x.ndim  # 获取x的维度数
    assert 0 <= 1 < ndim  # 确保x至少为2维【这里0<=1似乎也是冗余】

    # x形状一般为(batch_size, seq_len, n_heads, head_dim//2)
    # 这里确保freqs_cis与x的seq_len, head_dim//2维度一致, RoPE是对每个头分别进行的
    assert freqs_cis.shape == (x.shape[1], x.shape[-1])

    # 将第二维度和最后一维度分别变为seq_len和head_dim//2, 其余维度均为1，即(1, seq_len, 1, head_dim//2)
    shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
    return freqs_cis.view(*shape)


# 应用RoPE
def apply_rotary_emb(xq: torch.Tensor, xk: torch.Tensor, freqs_cis: torch.Tensor,) -> Tuple[torch.Tensor, torch.Tensor]:
    """应用RoPE, llama3是通过转换成复数形式来旋转角度的

    Args:
        xq (torch.Tensor): query
        xk (torch.Tensor): key
        freqs_cis (torch.Tensor): 旋转矩阵

    Returns:
        Tuple[torch.Tensor, torch.Tensor]: query和key的旋转结果
    """
    # 将xq和xk由(batch_size, seq_len, n_(kv)_heads, head_dim)转换为(batch_size, seq_len, n_(kv)_heads, head_dim//2, 2)
    # 即每个头的维度两两一组, 以此作为复数的实部和虚部, 转换为复数
    # xq_和xk_的形状为(batch_size, seq_len, n_(kv)_heads, head_dim//2), 里面保存的是复数, 这样转换后最后一维就与freqs_cis的最后一维一致了
    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))  # (batch_size, seq_len, n_heads, head_dim//2)
    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))  # (batch_size, seq_len, n_kv_heads, head_dim//2)

    # 按照xq_将freqs_cis的维度变为(1, seq_len, 1, head_dim//2)
    freqs_cis = reshape_for_broadcast(freqs_cis, xq_)

    # 通过复数乘法实现角度旋转
    # 复数张量转换为实数张量后, 通常为(..., 2)的形状, 即最后一维代表实部与虚部
    # 因此使用flatten将索引为3的维度展平, 形状由(batch_size, seq_len, n_(kv)_heads, head_dim//2, 2)变为(batch_size, seq_len, n_(kv)_heads, head_dim)
    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)  # (batch_size, seq_len, n_heads, head_dim)
    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)  # (batch_size, seq_len, n_kv_heads, head_dim)
    return xq_out.type_as(xq), xk_out.type_as(xk)

三、分组查询注意力机制GQA和KV Cache

（一）分组查询注意力机制GQA

Transformer中的 多头注意力（MHA） 在解码阶段来说是一个性能瓶颈。多查询注意力（MQA） 通过共享单个key和value头，同时不减少query头来提升性能，多查询注意力可能导致质量下降和训练不稳定。因此常用的是 分组查询注意力（GQA），它介于MHA和MQA之间，获得了与MHA相近的性能和与MQA相近的速度，下图直观的对此进行了表示。

【原文GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints的贡献主要包括两点：第一，对于已训练好的MHA模型，可以通过转换和微调来将其转换为MQA模型，从而提高推理速度；第二，提出GQA。】

（二）KV Cache

推理过程

🔥首先假设一个推理阶段的例子：

• 输入是“What color is the sky”，在大模型推理中输入也称为prompt
• 输出是“The sky is blue.“，在大模型推理中输出也称为completion

使用基于transformer的大模型，从上述prompt生成completion的过程分为如下几个步骤：

• 第1步，将大模型的模型权重加载到GPU的显存中
• 第2步，在CPU上对prompt做tokenization（分词），并将token的张量表示（token_ids）从内存传输到到GPU的显存中：

• 第3步，让token_ids走一遍网络得到输出的第一个token：

这一步只需要走一遍网络，也被称为prefill（预填充）阶段。

• 第4步，将生成的token拼接到输入的token的结尾，并以此作为一个新的输入来生成下一个token。重复上述过程，直到生成一个终止符的token或者达到配置的最大生成长度。终止符token也被称为end-of-sequence (EOS) token。

• 第5步，将生成的所有token从GPU的显存传输回CPU，然后由CPU将生成的id映射回文本，这就是最终生成的completion：
  

总的来说，大模型推理是一个两阶段的过程：

• 预填充（prefill）阶段：在这个阶段，模型处理输入的全部prompt，并进行前向计算。这个阶段的目的是生成第一个输出token，即响应的起始点。
• 解码（decoding）阶段：一旦prefill阶段完成，模型进入decoding阶段，逐个生成剩余的响应token。

对于预填充阶段和解码阶段可以使用以下性能评估指标：

• 预填充阶段的关键指标是 TTFT（Time To First Token），即生成第一个token所需的时间。
• 解码阶段的关键指标是 TPOT（Time Per Output Token），即生成每个响应token所需的平均时间。

这些指标对于评估和优化大模型推理性能至关重要。

KV Cache图示

在推理阶段，由于解码过程是一个token一个token的生成，每一次解码都从输入开始拼接好已经解码的token从而生成输入数据，然后预测下一个token，那么会有非常多的重复计算。因此通常使用KV Cache用于加速推理。

下图对比了 不使用 KV Cache和 使用 KV Cache的推理过程的区别：

或用以下动图表示：

不使用 KV Cache：

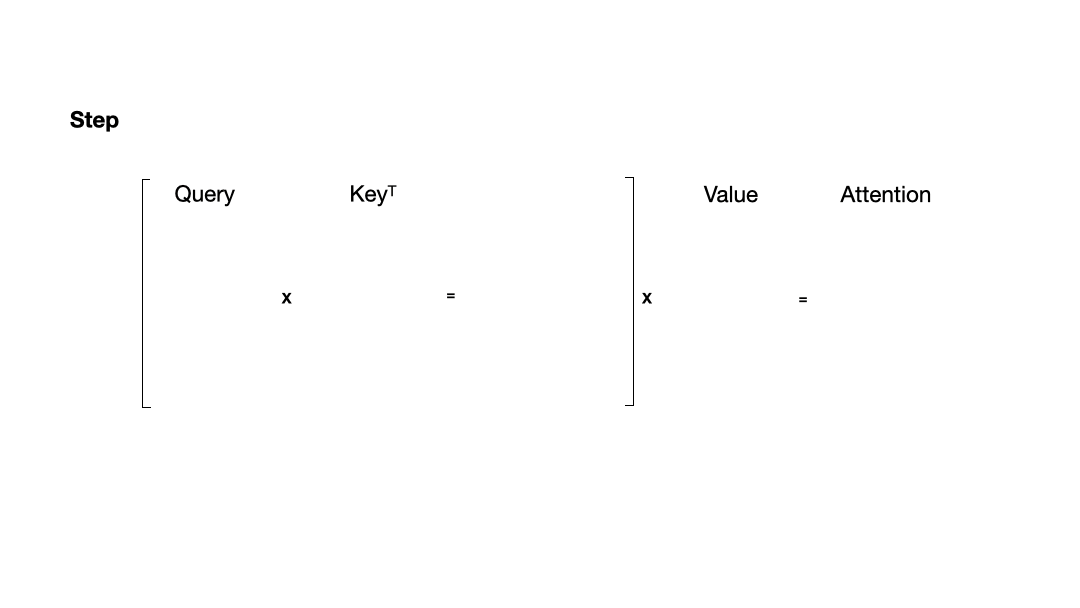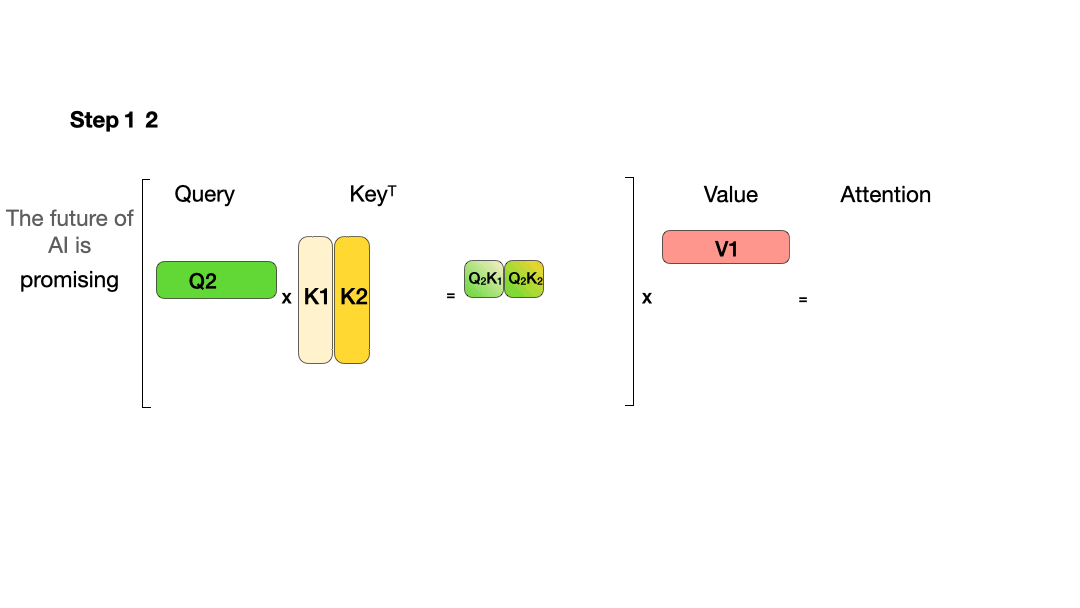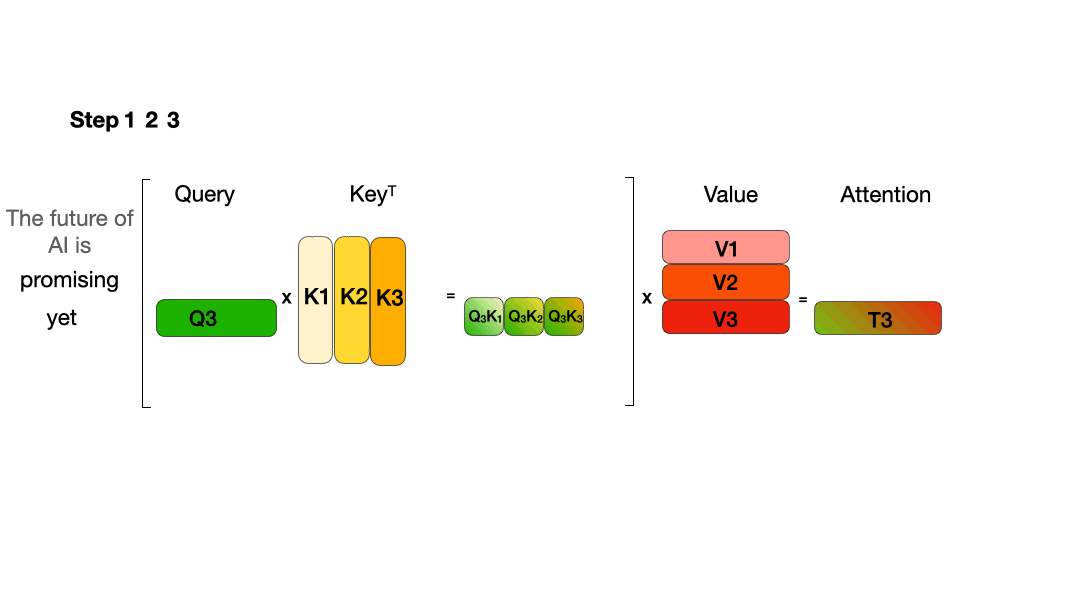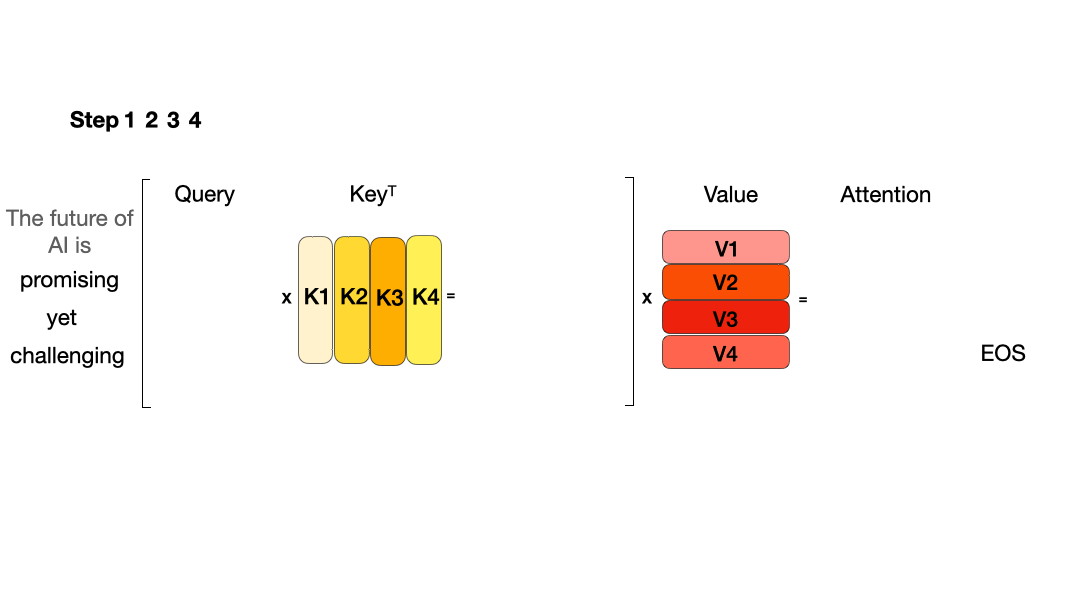
使用 KV Cache：

从图中可以看到，在每一步计算中，当前的查询向量 ($Q_i$) 都需要与之前的键向量 ($K_j$) 进行矩阵乘法计算，然后再与之前的值向量 ($V_j$) 进行矩阵乘法。为了节省计算资源，我们可以将之前计算得到的 ($K_j$) 和 ($V_j$) 结果缓存起来，从而使得每次计算时只需进行增量计算。这种缓存机制就是 KV Cache。

具体来说：

$$\begin{array}{rl}& Token1\to {\mathrm{Att}}_1(Q,K,V)=\mathrm{softmaxed}(Q_1{K}_1^T){\vec{V}}_1\\ & Token2\to {\mathrm{Att}}_2(Q,K,V)=\mathrm{softmaxed}(Q_2{K}_1^T){\vec{V}}_1+\mathrm{softmaxed}(Q_2{K}_2^T){\vec{V}}_2\\ & Token3\to {\mathrm{Att}}_3(Q,K,V)=\mathrm{softmaxed}(Q_3{K}_1^T){\vec{V}}_1+\mathrm{softmaxed}(Q_3{K}_2^T){\vec{V}}_2+\mathrm{softmaxed}(Q_3{K}_3^T){\vec{V}}_3\end{array}$$

根据上述图解与公式可发现：

• 对于 $Token1$ 的计算，由于 $Q_1{K}_2^T$ 和 $Q_1{K}_3^T$ 会mask掉，所以在计算 $Token1$ 时仅与 $Q_1$、$K_1$、$V_1$ 有关；
• 对于 $Token2$ 的计算，由于 $Q_2{K}_3^T$ 会mask掉，所以在计算 $Token2$ 时仅与 $Q_2$、$K_1$、$K_2$、$V_1$、$V_2$ 有关；
• 对于 $Token3$ 的计算，仅与 $Q_3$、$K_1$、$K_2$、$K_3$、$V_1$、$V_2$、$V_3$ 有关。

因此可以得出结论：

• ${\mathrm{Att}}_k(Q,K,V)$的计算主要与$Q_k$有关
• 每一次生成新的Token都需要用到之前的KV，所以我们需要把每一步的KV缓存起来

KV Cache的本质是以空间换时间，它 将历史输入token的KV缓存下来，避免每步生成都重新计算历史的KV值。一个典型的带有 KV cache 优化的生成大模型的推理过程包含了两个阶段：

1. 预填充阶段：输入一个prompt序列，为每个transformer层生成 key cache 和 value cache（KV cache），此步骤为并行同时计算序列的KV值
2. 解码阶段：使用之前的KV cache并计算当前的KV值，并将当前的KV值保存到cache中，然后生成token，仅需使用当前最后一个Q来计算，而无需将前面所有的Q拼接起来再计算。

（三）代码

# 复制kv heads
def repeat_kv(x: torch.Tensor, n_rep: int) -> torch.Tensor:
    """当key和value的头数量n_kv_heads小于查询头(query heads)数量时, 需要将key和value进行重复, 以匹配查询头的数量

    Args:
        x (torch.Tensor): key/value: (batch_size, seq_len, n_kv_heads, head_dim)
        n_rep (int): 重复的次数

    Returns:
        key/value: (batch_size, seq_len, n_kv_heads*n_rep, head_dim)
    """
    bs, slen, n_kv_heads, head_dim = x.shape
    if n_rep == 1:
        return x
    # x[:, :, :, None, :]用于插入一个维度, 使得形状变为: (batch_size, seq_len, n_kv_heads, 1, head_dim)
    # expand()用于扩展张量的维度, 使得形状变为: (batch_size, seq_len, n_kv_heads, n_rep, head_dim)
    return (
        x[:, :, :, None, :]
        .expand(bs, slen, n_kv_heads, n_rep, head_dim)
        .reshape(bs, slen, n_kv_heads * n_rep, head_dim)
    )


# 源码仅用于推理, 且使用了分布式训练方法, 这里进行了部分修改
class Attention(nn.Module):
    def __init__(self, args: CfgNode):
        super().__init__()
    
        # 此处考虑单卡, 使用常用的简单方式进行初始化
        self.args = args
        self.n_heads = args.MODEL.N_HEADS  # query的头数
        self.n_kv_heads = args.MODEL.N_HEADS if args.MODEL.N_KV_HEADS is None else args.MODEL.N_KV_HEADS  # key/value的头数, 未设置kv头数时, 默认与n_heads一致, 即MHA
        self.head_dim = args.MODEL.DIM // args.MODEL.N_HEADS
        self.n_rep = args.MODEL.N_HEADS // self.n_kv_heads  # query heads必须是kv heads的整数倍

        # 初始化权重矩阵
        self.wq = nn.Linear(args.MODEL.DIM, args.MODEL.N_HEADS * self.head_dim, bias=False, device=args.DEVICE)
        self.wk = nn.Linear(args.MODEL.DIM, self.n_kv_heads * self.head_dim, bias=False, device=args.DEVICE)
        self.wv = nn.Linear(args.MODEL.DIM, self.n_kv_heads * self.head_dim, bias=False, device=args.DEVICE)
        self.wo = nn.Linear(args.MODEL.N_HEADS * self.head_dim, args.MODEL.DIM, bias=False, device=args.DEVICE)  # GQA也产生n_heads个头的attention

        # 实现KV Cache, 用于存储KV矩阵, 包括prompt部分和生成部分的KV, 因此形状为(max_batch_size, max_seq_len*2, n_kv_heads, head_dim)
        self.cache_k = torch.zeros((args.TRAIN.BATCH_SIZE, args.MODEL.MAX_SEQ_LEN*2, self.n_kv_heads, self.head_dim), device=args.DEVICE)
        self.cache_v = torch.zeros((args.TRAIN.BATCH_SIZE, args.MODEL.MAX_SEQ_LEN*2, self.n_kv_heads, self.head_dim), device=args.DEVICE)

    # 源代码仅有推理模式, 这里区分训练与推理
    def forward(self, x: torch.Tensor, start_pos, inference, freqs_cis):
        # 输入维度为(batch_size, seq_len, dim)
        bsz, seq_len, _ = x.shape
        # mask只在训练时使用, 由于使用了KV Cache, 因此在推理模式下不需要使用mask
        mask = None
        
        # 由于只对线性层只对dim做变换，因此实际上跟seq_len无关，可以接受任意长度的seq_len
        xq = self.wq(x)  # (batch_size, seq_len, dim) -> (batch_size, seq_len, n_heads * head_dim)
        xk = self.wk(x)  # (batch_size, seq_len, dim) -> (batch_size, seq_len, n_kv_heads * head_dim)
        xv = self.wv(x)  # (batch_size, seq_len, dim) -> (batch_size, seq_len, n_kv_heads * head_dim)

        # 转换形状
        xq = xq.view(bsz, seq_len, self.n_heads, self.head_dim)      # (batch_size, seq_len, n_heads, head_dim)
        xk = xk.view(bsz, seq_len, self.n_kv_heads, self.head_dim)   # (batch_size, seq_len, n_kv_heads, head_dim)
        xv = xv.view(bsz, seq_len, self.n_kv_heads, self.head_dim)   # (batch_size, seq_len, n_kv_heads, head_dim)

        # 推理模式, KV Cache仅在推理模式下使用
        if inference:
            # 【推理模式中使用max_seq_len*2是为了同时容纳prompt和生成内容, 因此需要乘以2】
            # 【推理时只考虑当前位置token在序列长度范围内的旋转矩阵】
            freqs_cis = freqs_cis[start_pos : start_pos + seq_len]
            
            # xq:(batch_size, seq_len, n_heads, head_dim), xk:(batch_size, seq_len, n_kv_heads, head_dim)
            xq, xk = apply_rotary_emb(xq, xk, freqs_cis)

            self.cache_k = self.cache_k.to(xq)
            self.cache_v = self.cache_v.to(xq)

            # 将当前位置新产生的key和value存入KV Cache
            self.cache_k[:bsz, start_pos:start_pos + seq_len] = xk
            self.cache_v[:bsz, start_pos:start_pos + seq_len] = xv

            # 取出所有的历史key和value
            keys = self.cache_k[:bsz, :start_pos + seq_len]
            values = self.cache_v[:bsz, :start_pos + seq_len]

            # 使用repeat_kv函数将key/value的维度变为与query一致
            keys = repeat_kv(keys, self.n_rep)  # (batch_size, seq_len, n_heads, head_dim)
            values = repeat_kv(values, self.n_rep)  # (batch_size, seq_len, n_heads, head_dim)

        # 训练模式, 无需使用KV Cache
        else:
            # xq:(batch_size, seq_len, n_heads, head_dim), xk:(batch_size, seq_len, n_kv_heads, head_dim)
            # 预训练时，这里使训练的输入序列和freq_cis都按照max_seq_len进行计算，因此预训练的输入长度必须为max_seq_len
            # 而推理时，进行了freqs_cis = freqs_cis[start_pos : start_pos + seq_len]截取，因此可以接受任意长度的输入序列
            # 类比到transformer的绝对位置编码，实际也是可以计算更大的freqs_cis，然后根据序列长度来截取的
            xq, xk = apply_rotary_emb(xq, xk, freqs_cis)

            # 使用repeat_kv函数将key/value的维度变为与query一致
            keys = repeat_kv(xk, self.n_rep)  # (batch_size, seq_len, n_heads, head_dim)
            values = repeat_kv(xv, self.n_rep)  # (batch_size, seq_len, n_heads, head_dim)

            # 生成因果掩码(causal mask / sequence mask)
            mask = torch.full((seq_len, seq_len), float("-inf"), device=self.args.DEVICE)  # (seq_len, seq_len)的全为负无穷的张量
            mask = torch.triu(mask, diagonal=1).to(self.args.DEVICE)  # 生成上三角矩阵, 对角线上方不变, 对角线及下方全为0

        # 调整形状进行注意力计算
        xq = xq.transpose(1,2)  # (batch_size, n_heads, seq_len, head_dim)
        keys = keys.transpose(1,2)  # (batch_size, n_heads, seq_len, head_dim)
        values = values.transpose(1,2)  # (batch_size, n_heads, seq_len, head_dim)

        # 计算注意力分数
        scores = torch.matmul(xq, keys.transpose(2,3)).to(self.args.DEVICE)/math.sqrt(self.head_dim)  # (batch_size, n_heads, seq_len, seq_len)
        if mask is not None:
            scores = scores + mask

        # 应用softmax
        scores = F.softmax(scores.float(), dim=-1).type_as(xq)
        # 乘value
        output = torch.matmul(scores, values).to(self.args.DEVICE)  # (batch_size, n_heads, seq_len, head_dim)

        # (batch_size, n_heads, seq_len, head_dim) -> (batch_size, seq_len, n_heads * head_dim)
        output = output.transpose(1,2).contiguous().view(bsz, seq_len, -1)

        return self.wo(output)  # (batch_size, seq_len, n_heads * head_dim) -> (batch_size, seq_len, dim)

四、FFN和SwiGLU激活函数

SwiGLU结合了Swish和GLU两者的特点。

Swish是一个非线性激活函数，定义如下：

$$\text{Swish}(x)=x\ast \text{sigmoid}(\beta x)$$

其中，$\beta$为可学习参数。Swish可以比ReLU激活函数更好，因为它在0附近提供了更平滑的转换，这可以带来更好的优化。下图为不同$\beta$值对应的Swish激活函数图像：

GLU（Gated Linear Unit）定义为两个线性变换的分量积，其中一个线性变换由sigmoid激活。它其实不算是一种激活函数，而是一种神经网络层。它是一个线性变换后面接门控机制的结构。其中门控机制是一个sigmoid函数用来控制信息能够通过多少。

$$\text{GLU}(x)=\text{sigmoid}(Wx+b)\otimes (Vx+c)$$

LLM中常用的SwiGLU其实就是采用Swish作为激活函数的GLU变体：

$$\text{SwiGLU}(x)=\text{Swish}(Wx+b)\otimes (Vx+c)$$

使用SwiGLU函数构造一个前馈网络，不使用偏置项，有：

$$\text{FFNSwiGLU}(x)=W_2(\text{Swish}(W_{1}x)\otimes (W_{3}x))$$

Llama3中的前馈网络使用RMSNorm和残差结构，形成下图所示的框架：

代码如下：

# 前馈网络
class FeedForward(nn.Module):
    def __init__(self, dim:int, hidden_dim:int, multiple_of:int, ffn_dim_multiplier: Optional[float], args: CfgNode):
        super().__init__()
        self.dim = dim

        # 以下hidden dim计算方式源于源码, 用于保证hidden dim是256的倍数
        # 其中传入的初始hidden dim为4 * dim, multiple_of为256
        hidden_dim = int(2 * hidden_dim/3)
        if ffn_dim_multiplier is not None:
            hidden_dim = int(ffn_dim_multiplier * hidden_dim)
        hidden_dim = multiple_of * ((hidden_dim + multiple_of - 1) // multiple_of)

        # 定义线性层
        self.w1 = nn.Linear(self.dim, hidden_dim, bias=False, device=args.DEVICE)
        self.w2 = nn.Linear(hidden_dim, self.dim, bias=False, device=args.DEVICE)
        self.w3 = nn.Linear(self.dim, hidden_dim, bias=False, device=args.DEVICE)

    def forward(self, x):
        # (batch_size, seq_len, dim)
        return self.w2(F.silu(self.w1(x)) * self.w3(x))  # silu是beta=1的Swish

五、Transformer Block及整体模型

根据模型结构及上述代码，进而构造出完整的Llama3模型：

class TransformerBlock(nn.Module):
    def __init__(self, layer_id: int, args: CfgNode):
        super().__init__()
    
        # 定义参数
        self.args = args
        self.n_heads = args.MODEL.N_HEADS
        self.dim = args.MODEL.DIM
        self.head_dim = args.MODEL.DIM // args.MODEL.N_HEADS
        self.layer_id = layer_id
    
        # 定义attention部分
        self.attention = Attention(args)
        self.attention_norm = RMSNorm(args.MODEL.DIM, eps=args.MODEL.NORM_EPS)

        # 定义feedforward部分
        self.feed_forward = FeedForward(
            dim=args.MODEL.DIM,
            hidden_dim=4 * args.MODEL.DIM,
            multiple_of=args.MODEL.MULTIPLE_OF,
            ffn_dim_multiplier=args.MODEL.FFN_DIM_MULTIPLER,
            args=args,
            )
        self.ffn_norm = RMSNorm(args.MODEL.DIM, eps=args.MODEL.NORM_EPS)

    def forward(self, x, start_pos, inference, freqs_cis):
        # (batch_size, seq_len, dim)
        h = x + self.attention(self.attention_norm(x), start_pos, inference, freqs_cis)
        out = h + self.feed_forward(self.ffn_norm(h))
        return out


class Llama(nn.Module):
    def __init__(self, params: CfgNode):
        super().__init__()
        
        # 定义参数
        self.params = params

        # 定义embedding层
        self.tok_embeddings = nn.Embedding(params.MODEL.VOCAB_SIZE, params.MODEL.DIM)

        # 定义transformer模块
        self.layers = nn.ModuleList()
        for layer_id in range(params.MODEL.N_LAYERS):
            self.layers.append(TransformerBlock(layer_id=layer_id, args=params))

        # 定义输出模块的RMSNorm及线性层
        self.norm = RMSNorm(params.MODEL.DIM, eps = params.MODEL.NORM_EPS)
        self.output = nn.Linear(params.MODEL.DIM, params.MODEL.VOCAB_SIZE, bias=False)

        # 在模型初始化时，预先计算好旋转矩阵，区分训练时使用的旋转矩阵和推理时使用的旋转矩阵
        self.head_dim = params.MODEL.DIM // params.MODEL.N_HEADS
        freqs_cis_for_train = precompute_freqs_cis(
            dim=self.head_dim, 
            end=self.params.MODEL.MAX_SEQ_LEN, 
            theta=self.params.MODEL.ROPE_THETA
            )  # (max_seq_len, head_dim//2)
        freqs_cis_for_inference = precompute_freqs_cis(
            dim=self.head_dim, 
            end=self.params.MODEL.MAX_SEQ_LEN*2, 
            theta=self.params.MODEL.ROPE_THETA
            )  # (max_seq_len*2, head_dim//2)
        self.register_buffer('freqs_cis_for_train', freqs_cis_for_train.to(params.DEVICE))
        self.register_buffer('freqs_cis_for_inference', freqs_cis_for_inference.to(params.DEVICE))
        self.freqs_cis = None

    def forward(self, x, targets=None, start_pos=0):

        # start_pos: 推理模式下, 当前token的位置索引
        # x:(batch_size, seq_len) -> h:(batch_size, seq_len, dim)
        h = self.tok_embeddings(x)

        # 根据是否传入targets，确定是否是推理模式
        if targets is None:
            inference = True
            self.freqs_cis = self.freqs_cis_for_inference
        else:
            inference = False
            self.freqs_cis = self.freqs_cis_for_train

        # 依次传入各个transformer block
        for layer in self.layers:
            h = layer(h, start_pos, inference, self.freqs_cis)

        # 传入输出模块
        h = self.norm(h)
        # h:(batch_size, seq_len, dim) -> logits:(batch_size, seq_len, vocab_size)
        logits = self.output(h).float()
        loss = None

        # 如果是训练模式, 就计算loss
        if targets is None:
            loss = None
        else:
            # logits:(batch_size, seq_len, vocab_size)
            # targets:(batch_size, seq_len)
            loss = F.cross_entropy(logits.view(-1, self.params.MODEL.VOCAB_SIZE), targets.view(-1))

        return logits, loss  # 如果是推理模式, logits后续还需使用softmax产生概率分布

六、预训练

训练数据及过程主要参考：https://github.com/DLLXW/baby-llama2-chinese

由于算力资源有限，仅使用部分数据进行单卡训练。

数据链接：Baby-llama2-chinese Corpus，提取码：6unr。这里我们选择wiki、medical、baidubaike三个文件夹的语料，大约7GB多一点。这些数据提前进行了语料清洗，使用ChatGLM2-6B的tokenizer进行了分词处理，并转换成了token_id，样本之间用<eos>相分隔。这些数据将会进行拼接，形成一个形状为(num_tokens,)的一维数组，然后按照固定长度 max_length 进行分割，并形成形状为 (num_samples, max_length) 的二维数据集。

思考： 例如，如果 max_length=6，原始数据是：

[1, 2, 3, <eos>, 4, 5, 6, <eos>, 7, 8, 9, 0]

如果仅简单的重新排列形状，会被分割为：

[[1, 2, 3, <eos>, 4, 5],
 [6, <eos>, 7, 8, 9, 0]]

在这种情况下，数组的某一行可能出现跨样本的xxxx<eos>xxxx 形式。
在这种构造方式下可能出现的问题包括：

• 一行样本中间的 <eos> 可能对模型的学习造成干扰，尤其是当 <eos> 后的 token 实际上属于下一段文本时。
• 模型会尝试预测 <eos> 后的 token，这在真实情况下是不合理的。

如何解决这个问题？可以通过滑动窗口等方式来让模型在不同样本之间看到上下文，但这样也会使样本量急剧增加。本项目仅为了实现llama训练的一个基本流程，这里就简单的将数据直接进行重排划分。

通过预测下一个词，模型在预训练过程中，能够通过上文预测出<eos>，但<eos>的下文模型可能会产生一些无关的预测，好在我们通常在遇到<eos>后，就会停止生成，后面的无关预测也就不会产出了。

七、SFT微调

LLM微调的目的是将预训练模型中的知识引导出来的一种手段，通俗的讲就是教会模型说人话。

微调方法：自然语言处理目前存在一个重要的范式：一般领域数据的大规模预训练，对特定任务或领域的适应。因此，为了让预训练模型在特定任务或领域有不错的表现，需要对模型进行微调。目前主流的四种微调方法如下：

• 全面微调（Full Fine-tuning）：使用任务特定数据调整LLM的所有参数。
• 参数高效精细调整（Parameter Efficient Fine-tuning）：修改选定参数以实现更高效的适应。例如：LoRA、Adapter、Prefix-tuning、P-tuning以及P-tuning v2。
• 提示工程（Prompt Engineering）：改进模型输入以指导模型输出理想结果。
• 检索增强生成（Retrieval Augmented Generation）：将提示工程与数据库查询结合，以获得丰富的上下文答案。

其中Full Fine-tuning和Parameter Efficient Fine-tuning是需要基于特定任务或者垂直领域数据对模型（全部 or 部分）参数进行微调； Prompt Engineering和Retrieval Augmented Generation是通过设计模型输入的template，引导模型输出我们想要的内容，不需要对模型参数进行微调。其中RAG是通过外挂数据库的方式，为模型提供领域知识输入。

由于本项目模型参数并不大，因此选择Full Fine-tuning对特定任务或领域数据进行微调。

数据链接：

https://huggingface.co/datasets/shibing624/alpaca-zh

https://huggingface.co/datasets/BelleGroup/train_1M_CN

SFT的逻辑如下：

• prompt和answer之间一定要有一个开始符<bos>隔开，然后answer后需要一个结束符<eos>
• sft训练时，相当于让模型对prompt+<bos>+answer+<eos>这个序列执行预测下一个字符，这个序列长度短于max_seq_len
• 计算loss的时候，对prompt+<bos>部分的loss进行mask，只计算answer部分的loss
• <bos>的主要作用是划分输入的结构边界，而非需要生成的内容，它的存在为模型提供了明确的上下文分段信号
• 模型需基于完整输入（包括 <bos>）预测后续 token，间接学习到 <bos> 的引导作用
• <bos>只是定义方式的一种，这里可以命名为任何特殊字符，例如<sep>等

参考链接

1. The Llama 3 Herd of Models【Llama3】
2. Root Mean Square Layer Normalization【RMSNorm】
3. RoFormer: Enhanced Transformer with Rotary Position Embedding【RoPE】
4. 图解RoPE旋转位置编码及其特性
5. GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints【GQA】
6. 大模型推理加速与KV Cache（一）：什么是KV Cache
7. LLM推理优化 - KV Cache
8. KV Cache：图解大模型推理加速方法
9. LLM Inference Series: 2. The two-phase process behind LLMs’ responses
10. Transformers KV Caching Explained
11. https://github.com/meta-llama/llama3
12. https://github.com/DLLXW/baby-llama2-chinese
13. https://github.com/tamangmilan/llama3
14. GLU Variants Improve Transformer【SwiGLU】
15. https://github.com/DLLXW/baby-llama2-chinese