完全背包问题

先贴一段完全背包的介绍:

背包问题是一个经典的动态规划问题，它的核心思想是在背包容量有限的情况下，如何选择一些重量和价值不同的物品，使得选择的物品在不超过背包容量的前提下，总价值最大。完全背包是背包问题的一种变种，不同之处在于每种物品的数量是无限的，即可以重复选择。

动态规划的核心思想是将原问题分解成各个子问题并以递推的方式求解这些子问题。对于完全背包问题来说，总的问题就是“在背包容情况下，如何选择一些重量和价值不同的物品，使得选择的物品在不超过背包容量的前提下，总价值最大”，而每个子问题就是“在容量为i的背包中，选择一些物品，使得它们的总重量不超过i的前提下，总价值最大”。 在实现过程中物品中选择物品的最大总价值。那么，f[i][j]可以分为两个情况：

1. 不另选择第i个物品，即f[i][j] = f[i-1][j]
2. 又选择一个第i个物品，即f[i][j] = f[i][j-w[i]] + v[i]

---

下面我们用表格来讲解一下

数据:

	重量	价值
1	2	3
2	4	7
3	3	6

可得表格

补全之后是

现在取f[3][4]进行分析

可以看出这个点是从f[3-1][4]得来的,于是就证明了前面说的不再选择第i个物品，即f[i][j] = f[i-1][j]
再取f[3][3]进行分析

可以看出这个点不是不再选第三个物品(f[i][j] = f[i-1][j])得来的,那就是一定再选一个第三个物品,,所以背包空间要先减去w[i],因为还是选前i件物品,只不过另外又选了一次,所以知道是由f[i][j-w[i]]得来的,最终得又选择一个第i个物品，即f[i][j] = f[i][j-w[i]] + v[i]

---

综上所述,得到代码

#include<all>
using namespace std;
long long n, m;       // 种类,容量
long long w[1010];      // 重量
long long v[1010];      // 价值
long long f[1010]; // 前i件物品,容量为j的最大价值
int main()
{
    cin >> m >> n;
    for(long long i=1;i<=n;i++){
        cin>>w[i]>>v[i];
    }
    for(long long i=1;i<=n;i++){
        for(long long j=m;j>=w[i];j--){
            
                f[j]=max(f[j],f[j-w[i]]+v[i]);
        }
    }
    cout<<f[m];
    return 0;
}

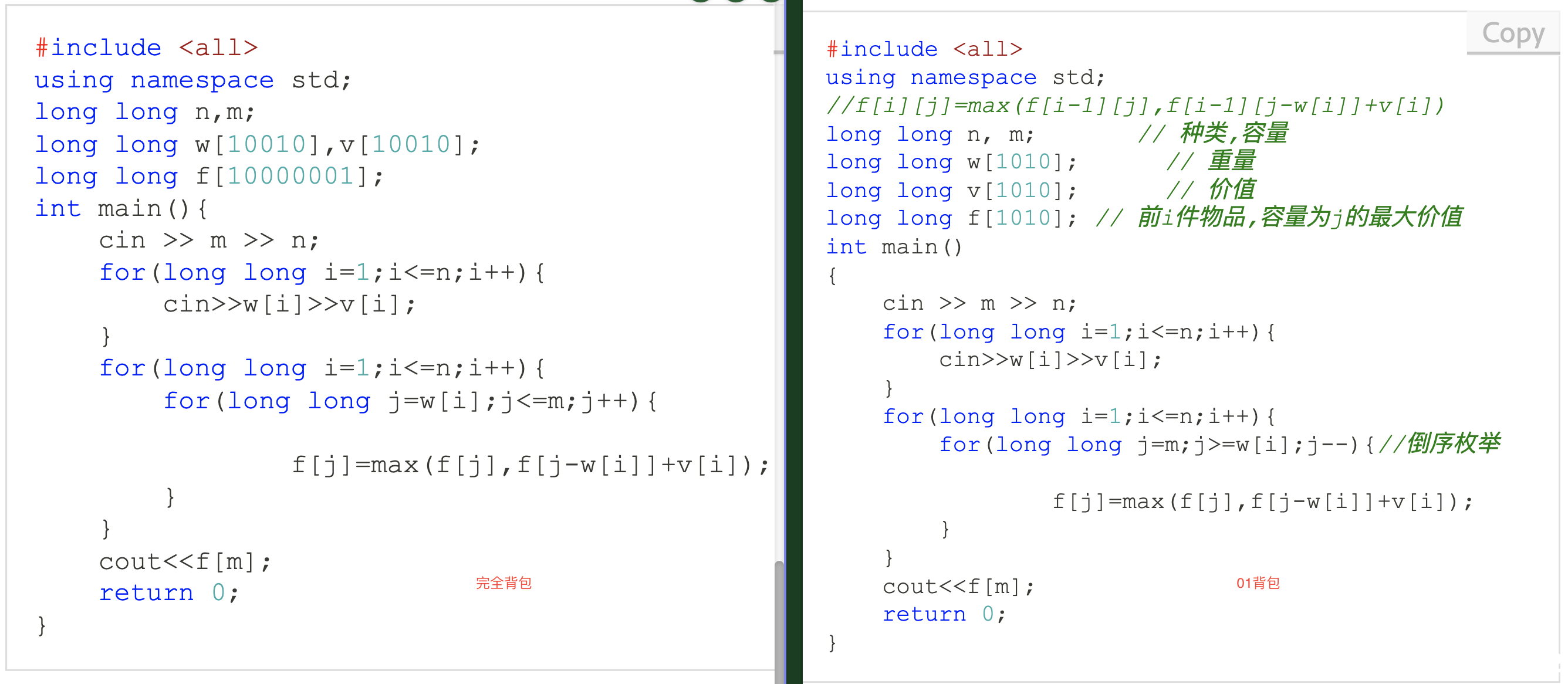
再结合01背包进行空间优化,可以得到

#include <all>
using namespace std;
long long n,m;
long long w[10010],v[10010];
long long f[10000001];
int main(){
    cin >> m >> n;
    for(long long i=1;i<=n;i++){
        cin>>w[i]>>v[i];
    }
    for(long long i=1;i<=n;i++){
        for(long long j=w[i];j<=m;j++){
            
                f[j]=max(f[j],f[j-w[i]]+v[i]);
        }
    }
    cout<<f[m];
    return 0;
}

---

比较一下01背包和完全背包