LeetCode 1504. 统计全 1 子矩形

1504. 统计全 1 子矩形

给你一个 m x n 的二进制矩阵 mat ，请你返回有多少个 子矩形 的元素全部都是 1 。

示例 1：

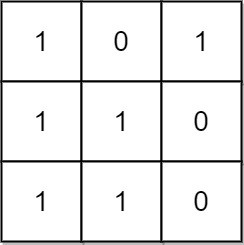
输入：mat = [[1,0,1],[1,1,0],[1,1,0]]
输出：13
解释：
有 6 个 1x1 的矩形。
有 2 个 1x2 的矩形。
有 3 个 2x1 的矩形。
有 1 个 2x2 的矩形。
有 1 个 3x1 的矩形。
矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。

示例 2：

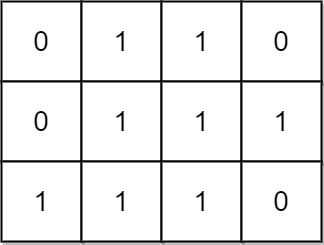
输入：mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]]
输出：24
解释：
有 8 个 1x1 的子矩形。
有 5 个 1x2 的子矩形。
有 2 个 1x3 的子矩形。
有 4 个 2x1 的子矩形。
有 2 个 2x2 的子矩形。
有 2 个 3x1 的子矩形。
有 1 个 3x2 的子矩形。
矩形数目总共 = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24 。

提示：

• 1 <= m, n <= 150
• mat[i][j] 仅包含 0 或 1

---

提示 1

For each row i, create an array nums where: if mat[i][j] == 0 then nums[j] = 0 else nums[j] = nums[j-1] +1.

---

提示 2

In the row i, number of rectangles between column j and k(inclusive) and ends in row i, is equal to SUM(min(nums[j, .. idx])) where idx go from j to k. Expected solution is O(n^3).

 

解法1：枚举

首先很直观的想法，我们可以枚举矩阵中的每个位置 (i,j)，统计以其作为右下角时，有多少个元素全部都是 1 的子矩形，那么我们就能不重不漏地统计出满足条件的子矩形个数。那么枚举以后，我们怎么统计满足条件的子矩形个数呢？

既然是枚举以 (i,j) 作为右下角的子矩形个数，那么我们可以直接暴力地枚举左上角 (k,y)，看其组成的矩形是否满足条件，时间复杂度为 O(nm)。但这样无疑会使得时间复杂度变得很高，我们需要另寻他路。

我们预处理 row 数组，其中 nums[i][j] 代表矩阵中 (i,j) 向左延伸连续 1 的个数，容易得出递推式：
​mat[i][j]=0 时, nums[i][j]=0
mat[i][j]=1 时, nums[i][j]=nums[i][j−1]+1,
 
有了 nums 数组以后，如果要统计以 (i,j) 为右下角满足条件的子矩形，我们就可以枚举子矩形的高，即第 k 行，看当前高度有多少满足条件的子矩形。由于我们知道第 k 行到第 i 行「每一行第 j 列向左延伸连续 1 的个数」 nums[k][j],nums[k+1][j],⋯,nums[i][j]，因此我们可以知道第 k 行满足条件的子矩形个数就是这些值的最小值，它代表了「第 k 行到第 i 行子矩形的宽的最大值」，公式化来说，即：

min(nums[k ... i][j])
因此我们倒序枚举 k，用 col 变量来记录 nums[k][j] 到当前行 nums[i][j] 的最小值，即能在 O(n) 的时间内统计出以 (i,j) 为右下角满足条件的子矩形个数。

Java版：

class Solution {
    public int numSubmat(int[][] mat) {
        int m = mat.length;
        int n = mat[0].length;
        int[][] nums = new int[m][n];
        int ans = 0;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (mat[i][j] == 1) {
                    if (j == 0) {
                        nums[i][j] = 1;
                    } else {
                        nums[i][j] = nums[i][j - 1] + 1;
                    }
                }
            }
        }
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                ans += nums[i][j];
                int col = nums[i][j];
                for (int k = i - 1; k >= 0; k--) {
                    col = Math.min(col, nums[k][j]);
                    ans += col;
                }
            }
        }
        return ans;
    }
}

Python3版：

class Solution:
    def numSubmat(self, mat: List[List[int]]) -> int:
        m = len(mat)
        n = len(mat[0])
        nums = [[0] * n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                if mat[i][j] == 1:
                    if j == 0:
                        nums[i][j] = 1
                    else:
                        nums[i][j] = nums[i][j - 1] + 1
        
        ans = 0
        for i in range(m):
            for j in range(n):
                ans += nums[i][j]
                col = nums[i][j]
                for k in range(i - 1, -1, -1):
                    col = min(col, nums[k][j])
                    ans += col
        return ans

复杂度分析

• 时间复杂度：O(n^2 * m)，其中 n 为矩阵行数，m 为矩阵列数。我们预处理 nums 数组需要 O(mn) 的时间，统计答案的时候一共需要枚举 O(mn) 个位置，每次枚举的时候需要 O(n) 的时间计算，因此时间复杂度为 O(n^2 * m)，故总时间复杂度为 O(nm+n^2 * m)=O(n^2 * m)。
• 空间复杂度：O(nm)。我们需要 O(nm) 的空间来存储 nums 数组。