LeetCode 2132. 用邮票贴满网格图

2132. 用邮票贴满网格图

给你一个 m x n 的二进制矩阵 grid ，每个格子要么为 0 （空）要么为 1 （被占据）。

给你邮票的尺寸为 stampHeight x stampWidth 。我们想将邮票贴进二进制矩阵中，且满足以下 限制 和 要求 ：

1. 覆盖所有 空 格子。
2. 不覆盖任何 被占据 的格子。
3. 我们可以放入任意数目的邮票。
4. 邮票可以相互有 重叠 部分。
5. 邮票不允许 旋转 。
6. 邮票必须完全在矩阵 内 。

如果在满足上述要求的前提下，可以放入邮票，请返回 true ，否则返回 false 。

示例 1：

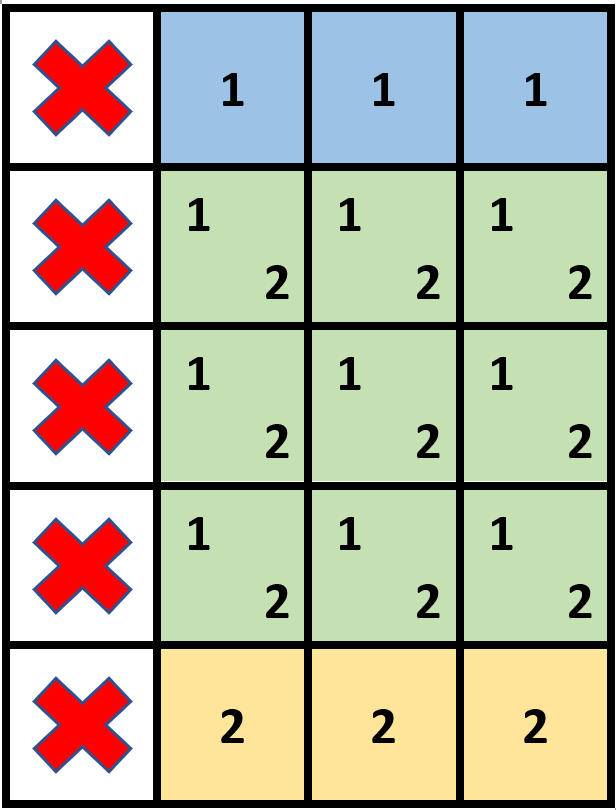
输入：grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], stampHeight = 4, stampWidth = 3
输出：true
解释：我们放入两个有重叠部分的邮票（图中标号为 1 和 2），它们能覆盖所有与空格子。

示例 2：

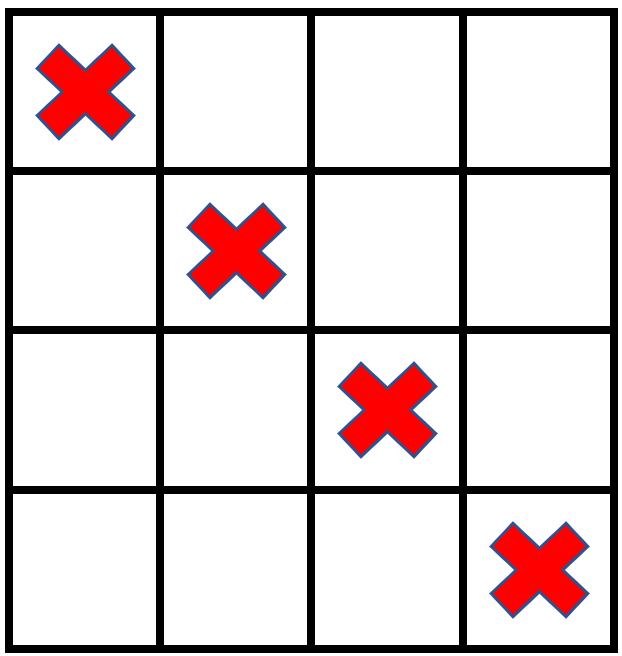
输入：grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], stampHeight = 2, stampWidth = 2 
输出：false 
解释：没办法放入邮票覆盖所有的空格子，且邮票不超出网格图以外。

提示：

• m == grid.length
• n == grid[r].length
• 1 <= m, n <= 10^5
• 1 <= m * n <= 2 * 10^5
• grid[r][c] 要么是 0 ，要么是 1 。
• 1 <= stampHeight, stampWidth <= 10^5

---

提示 1

We can check if every empty cell is a part of a consecutive row of empty cells that has a width of at least stampWidth as well as a consecutive column of empty cells that has a height of at least stampHeight.

---

提示 2

We can prove that this condition is sufficient and necessary to fit the stamps while following the given restrictions and requirements.

---

提示 3

For each row, find every consecutive row of empty cells, and mark all the cells where the consecutive row is at least stampWidth wide. Do the same for the columns with stampHeight. Then, you can check if every cell is marked twice.

解法1：二维前缀和 + 二维差分数组

思路
由于邮票可以互相重叠，贪心地想，能放邮票就放邮票。
遍历所有能放邮票的位置去放邮票。注意邮票不能覆盖被占据的格子，也不能出界。
放邮票的同时，记录每个空格子被多少张邮票覆盖。如果存在一个空格子没被邮票覆盖，则返回 false，否则返回 true。

怎么快速判断一个矩形区域可以放邮票？

求出 grid 的二维前缀和，从而 O(1) 地求出任意矩形区域的元素和。如果一个矩形区域的元素和等于 0，就表示该矩形区域的所有格子都是 0。
假设用一个二维计数矩阵 cnt 记录每个空格子被多少张邮票覆盖，那么放邮票时，就需要把 cnt 的一个矩形区域都加一。

怎么快速实现？

可以用二维差分矩阵 diff 来代替 cnt。矩形区域都加一的操作，转变成 O(1) 地对 diff 中四个位置的更新操作。
最后从二维差分矩阵 diff 还原出二维计数矩阵 cnt。类似对一维差分数组求前缀和得到原数组，我们需要对二维差分矩阵求二维前缀和。遍历 cnt，如果存在一个空格子的计数值为 0，就表明该空格子没有被邮票覆盖，返回 false，否则返回 true。代码实现时，可以直接在 diff 数组上原地计算出 cnt。

Java版：

class Solution {
    public boolean possibleToStamp(int[][] grid, int stampHeight, int stampWidth) {
        int m = grid.length;
        int n = grid[0].length;

        // 1. 计算 grid 的二维前缀和
        int[][] presum = new int[m + 1][n + 1];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                presum[i + 1][j + 1] = presum[i + 1][j] + presum[i][j + 1] - presum[i][j] + grid[i][j];
            }
        }

        // 2. 计算二维差分
        // 为方便第 3 步的计算，在 diff 数组的最上面和最左边各加了一行（列），所以下标要 +1
        int[][] diff = new int[m + 2][n + 2];
        for (int i2 = stampHeight; i2 <= m; i2++) {
            for (int j2 = stampWidth; j2 <= n; j2++) {
                int i1 = i2 - stampHeight + 1;
                int j1 = j2 - stampWidth + 1;
                if (presum[i2][j2] - presum[i2][j1 - 1] - presum[i1 - 1][j2] + presum[i1 - 1][j1 - 1] == 0) {
                    diff[i1][j1]++;
                    diff[i1][j2 + 1]--;
                    diff[i2 + 1][j1]--;
                    diff[i2 + 1][j2 + 1]++;
                }
            }
        }

        // 3. 还原二维差分矩阵对应的计数矩阵（原地计算）
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                diff[i + 1][j + 1] += diff[i + 1][j] + diff[i][j + 1] - diff[i][j];
                if (grid[i][j] == 0 && diff[i + 1][j + 1] == 0) {
                    return false;
                }
            }
        } 
        return true;
    }
}

Python3版：

class Solution:
    def possibleToStamp(self, grid: List[List[int]], stampHeight: int, stampWidth: int) -> bool:
        m = len(grid)
        n = len(grid[0])

        # 1. 计算 grid 的二维前缀和
        presum = [[0] * (n + 1) for _ in range(m + 1)]
        for i, row in enumerate(grid):
            for j, v in enumerate(row):
                presum[i + 1][j + 1] = presum[i + 1][j] + presum[i][j + 1] - presum[i][j] + v 
        
        # 2. 计算二维差分
        # 为方便第 3 步的计算，在 diff 数组的最上面和最左边各加了一行（列），所以下标要 +1
        diff = [[0] * (n + 2) for _ in range(m + 2)]
        for i2 in range(stampHeight, m + 1):
            for j2 in range(stampWidth, n + 1):
                i1 = i2 - stampHeight + 1
                j1 = j2 - stampWidth + 1
                if presum[i2][j2] - presum[i2][j1 - 1] - presum[i1 - 1][j2] + presum[i1 - 1][j1 - 1] == 0:
                    diff[i1][j1] += 1
                    diff[i1][j2 + 1] -= 1
                    diff[i2 + 1][j1] -= 1
                    diff[i2 + 1][j2 + 1] += 1
        
        # 3. 还原二维差分矩阵对应的计数矩阵（原地计算）
        for i, row in enumerate(grid):
            for j, v in enumerate(row):
                diff[i + 1][j + 1] += diff[i + 1][j] + diff[i][j + 1] - diff[i][j]
                if v == 0 and diff[i + 1][j + 1] == 0:
                    return False 
        return True

复杂度分析

• 时间复杂度：O(mn)，其中 m 和 n 分别为 grid 的行数和列数。
• 空间复杂度：O(mn)。