问题描述:在一个的方格组成的棋盘中,有一个方格与其他的方格不同,称之为奇异块。要求:若使用一下四种L型骨牌覆盖除这个奇异块的其他方格,覆盖过程中L型骨牌之间不能有互相覆盖,设计算法求出覆盖方案。(四种L型骨牌如下图)
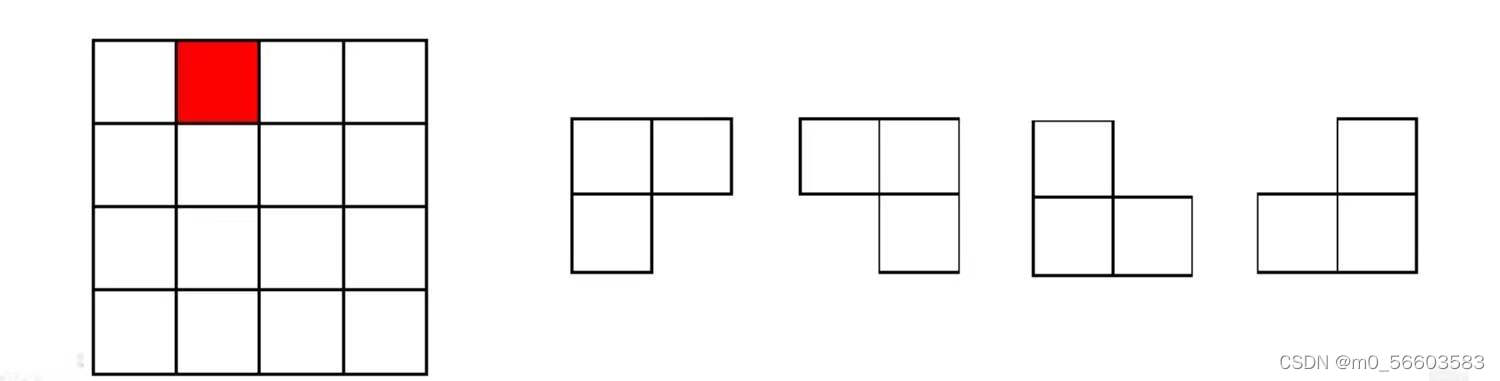
算法思想:分治法。
分治法原理:1.划分2.求解3.合并。将原始问题分解为如果个互不相同的子问题,对子问题进行求解。
(1)解题思路:
1.当k>0时,可以将 棋盘由中心划分为对称的四份
小棋盘(子问题划分)
此时,我们很容易知道奇异块一定在其中一个子棋盘中,其他三个相邻的子棋盘没有奇异块。Divide
2.使用一个合适的L型骨牌,覆盖三个没有奇异块的子方格(覆盖方法及L型骨牌的选取:将L型骨牌i在中心处覆盖。可参考下图)将覆盖的L型骨牌在其余三个子棋盘中视为奇异块,我们便得到了4个
的棋盘覆盖问题。
3.继续递归处理四个子棋盘直到划分的子棋盘恰好为一个奇异块为止。Conquer
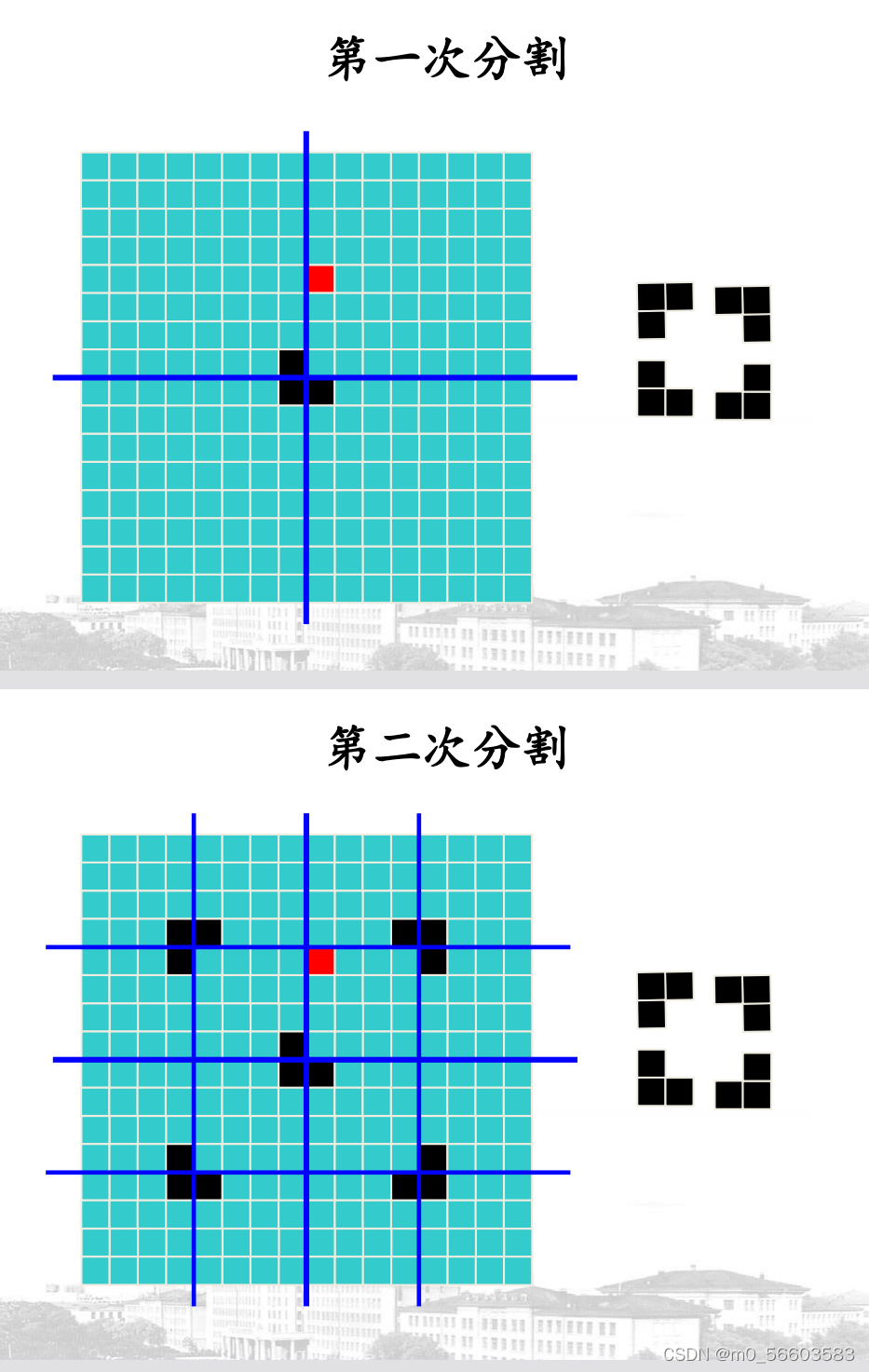
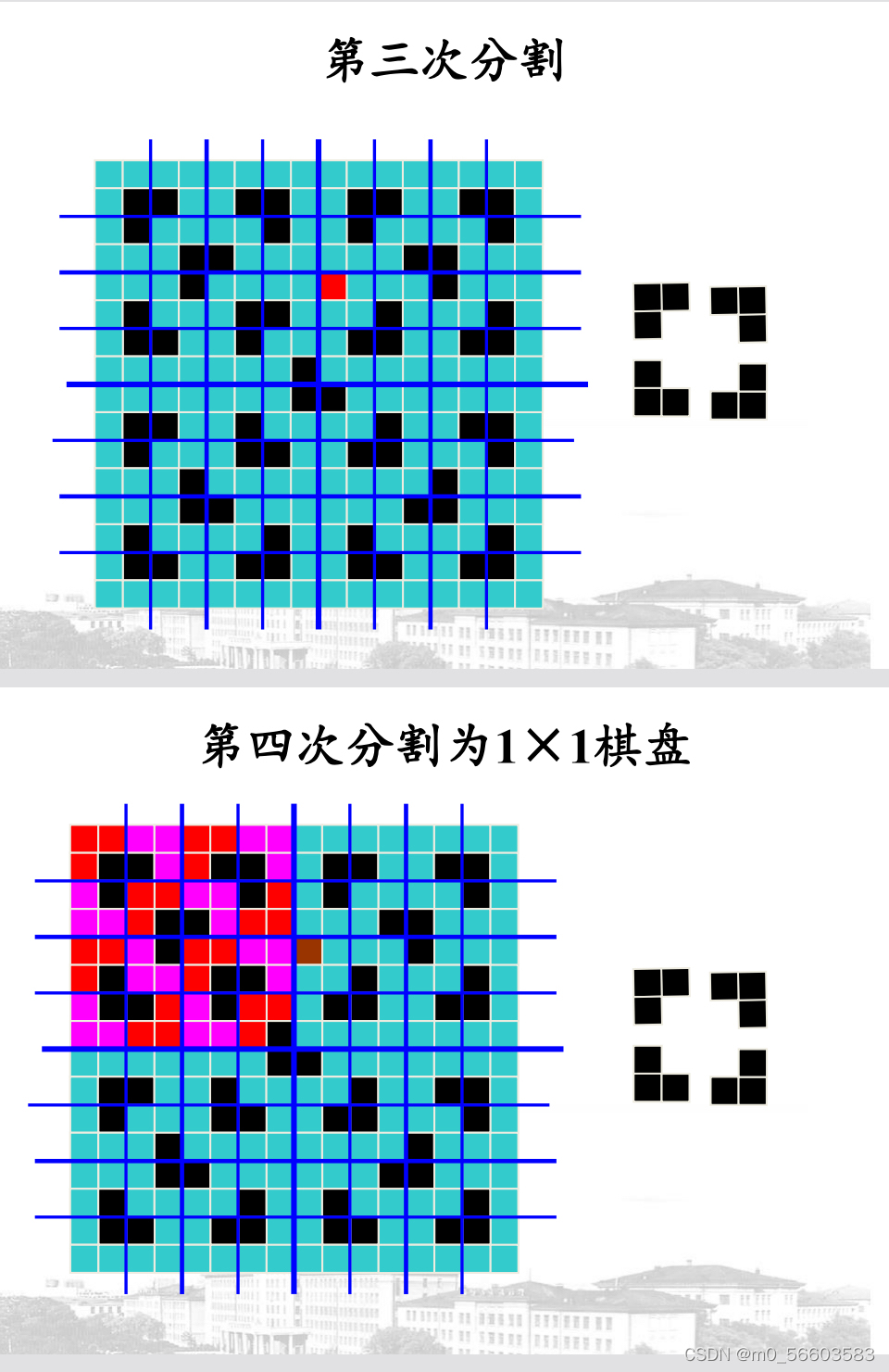
(2)c++代码实现(伪代码):
算法:
ChessBoard(tr,tc,dr,dc,n)
全局变量:
tile = 1;//被覆盖的方格记号
Board[n][n]=0;//标记棋盘被覆盖的方格
输入:
tr,tc;//棋盘的左上角行号、列号
dr,dc;//特殊方格行号、列号
n;//棋盘尺寸n*n
执行:
ChessBoard(0,0,dr,dc,k)
/*****************************************************************************************/
ChessBoard(tr,tc,dr,dc,n)
{
if(k==0)
return;
t = tile++;
n = n/2;
//1.检验左上角是否有奇异块
if(dr<tr+n&&dc>tc+n)
{
ChessBoard(tr,tc,dr,dc,n);
}//奇异块在此棋盘之中(左上角)
else
{
Board[tr+n-1][tc+n-1] = tile;//将该方格覆盖并标记
ChessBoard(tr,tc,tr+n-1,tc+n-1,n);//对左上角进行递归(将新覆盖的方格视为奇异块)
}
//2.检验右上角
if(dr<tr+n&&dc>=tc+n)
{
ChessBoard(tr,tc+n,dr,dc,n);
}
else
{
Board[tr+n-1][tc+n] = tile;
ChessBoard(tr,tc+n,tr+n-1,tc+n,n);
}
//3.检验左下角
if(dr>=tr+n&&dc<tc+n)
{
ChessBoard(tr+n,tc,dr,dc,n);
}
else
{
Board[tr+n][tc+n-1] = tile;
ChessBoard(tr+n,tc,tr+n,tc+n-1,n);
}
//4.检验右下角
if(dr>=tr+n&&dc>=tc+n)
{
ChessBoard(tr+n,tc+n,dr,dc,n);
}
else
{
Board[tr+n][tc+n] = tile;
ChessBoard(tr+n,tc+n,tr+n,tc+n,n);
}
}注释:理解算法代码中的连串if-else语句非常重要!
(示意图:供理解和参考)
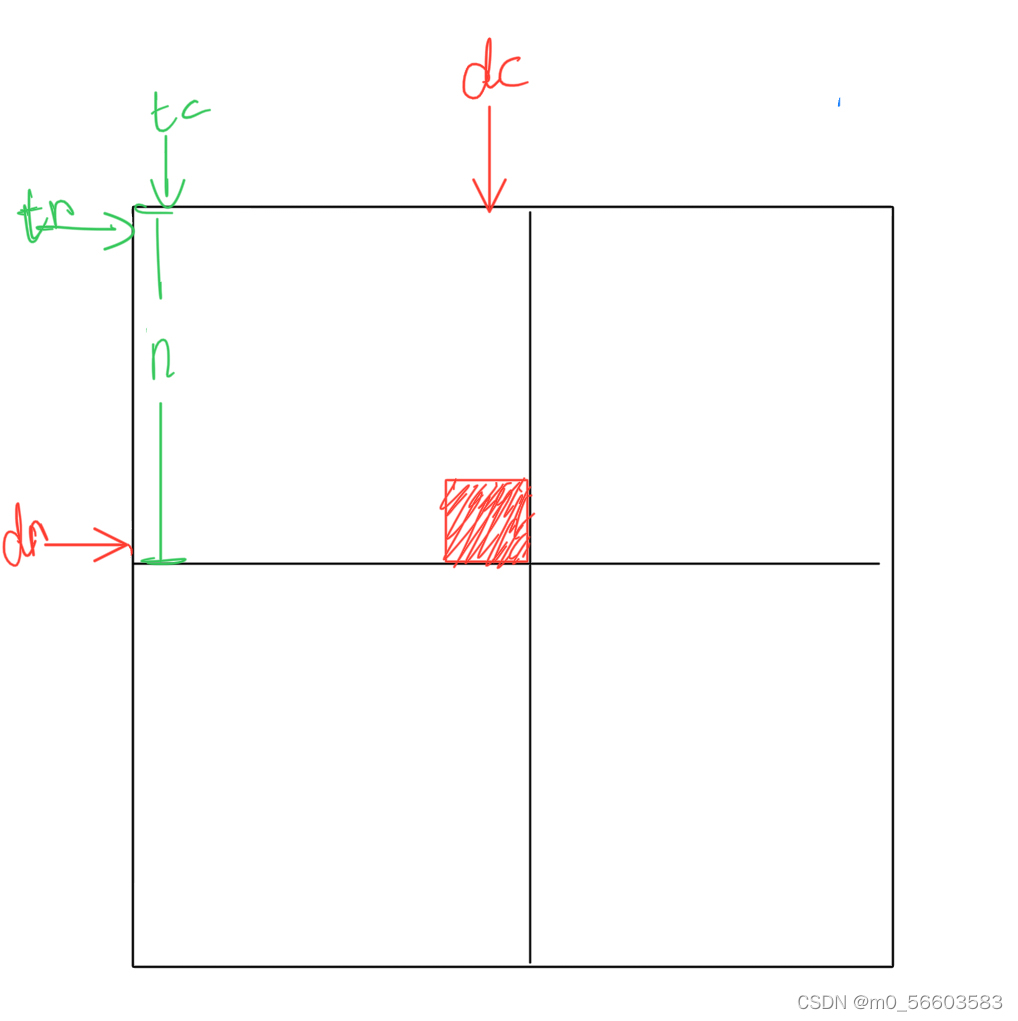







 本文介绍了一种使用L型骨牌覆盖除奇异块外的棋盘方格的算法。采用分治策略,通过递归地将棋盘划分成更小的部分,并用一个L型骨牌覆盖未含有奇异块的小棋盘的中心,最终解决整个覆盖问题。
本文介绍了一种使用L型骨牌覆盖除奇异块外的棋盘方格的算法。采用分治策略,通过递归地将棋盘划分成更小的部分,并用一个L型骨牌覆盖未含有奇异块的小棋盘的中心,最终解决整个覆盖问题。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








