激光光谱与量子光学原理-第七章-CSDN博客

非线性问题的具体体现：在外加场的最低阶近似下，原子偶极子在所有外加场的频率上都有响应，这与线性情况相同。然而，在场的二阶近似下，态的布居会发生变化，这种变化取决于每对场的拍频。在更高阶近似下，许多不同的场频率组合都会出现。因此，解决任意强度且频率不同的两个或多个场与两能级原子相互作用问题的唯一方法是进行数值求解。

解析解获得方式：利用微扰理论或者当只有某一个场为强场其余场为弱场。

推导过程：

1. 给出总的场表达式

2. 计算总场场强

其中

3. 给出密度函数矩阵的相互作用表象（the interaction representation）方程组

考虑的场景是单一种类原子和多个频率的外加场，因此采用相互作用表象。

其中

与之前不同的是，上方程组中与外加场相关的量均变成了求和形式。这些方程可以通过以外部场振幅为幂的微扰级数来求解。本章节中感兴趣的是稳态响应，意味着密度矩阵元素的值是所有跃迁都完成后的值。由之前的章节可知， $\varrho_{\alpha\alpha^{\prime}}(\mathbf{R},\mathbf{v},t)$ 是单个量子的密度矩阵元素。整体的相空间密度矩阵的元素由以下公式给出：

其中 $\mathcal{N}(\mathbf{R})$ 是空间密度， $W_0(\mathbf{v})$ 是没有任何外加场时的速度分布。

7.1.1 零阶（Zeroth Order）

在外加场的零阶近似下，即忽略所有外加场的作用，只考虑量子系统本身的静态行为，原子的密度矩阵元素弛豫到其平衡值， $\varrho_{11}(\mathbf{R},\mathbf{v},t)=1,\varrho_{21}^{I}(\mathbf{R},\mathbf{v},t)=\varrho_{12}^{I}(\mathbf{R},\mathbf{v},t)=\varrho_{22}(\mathbf{R},\mathbf{v},t)=0$ 。

7.1.2 一阶（First Order）

对于外加场的一阶近似，假定解的形式为：

将其带入（7.4a）化简得到：

上述公式求解时需要带入零阶近似中的 $\varrho_{22}(\mathbf{R},\mathbf{v},t)=0$

对于一阶量来说，该响应是各个场贡献的总和；该响应是线性的，并且遵循叠加原理。

7.1.3 二阶（Second Order）

对于二阶近似，假定解的形式为：

同样，将（7.7），（7.8），（7.9）带入（7.4b）中化简得到：

其中 $\gamma=\gamma_2/2+\Gamma$ 。

如果：

则

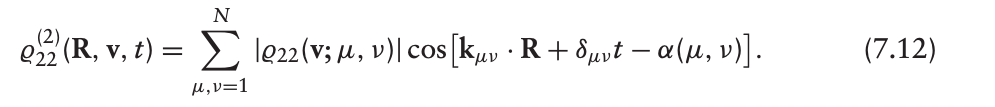
由于密度矩阵是物理实量（Observable），我们只取其实部。

粒子布居包含一个恒定的背景项，以及一组移动的光学光栅（干涉条纹）。而这些光栅的相位，一般会相对于入射场强的“移动驻波”存在偏移。这说明原子的响应不是瞬时的，而是带有记忆和滞后的，结果就是布居的周期性调制和入射光场的干涉图样之间并不同步（存在相位偏移）。

7.1.4 三阶（Third Order）

对于三阶近似，假定解的形式为：

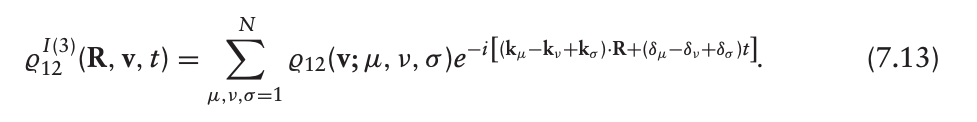
同样，将之前的（7.9）和（7.13）带入（7.4a），化简得到：

每一个可能的 $\mu,\nu,\sigma$ 都对应于对三阶极化的一个贡献；对于 $N$ 个场，存在 $N^{3}$ 个这样的贡献。

（7.14）提供了丰富的信息，可以用于分析成堆的问题。以下进行分情况讨论：

1. $\mu=\nu$

此时， $\mathbf{k}_s=\mathbf{k}_\sigma$ ，这意味着 $\varrho_{12}^{I(3)}(\mathbf{R},\mathbf{v},t)$ 随 $e^{-i(\mathbf{k}_\sigma\cdot\mathbf{R}-\omega_\sigma t)}$ 变化。也就是说，这种贡献来自于修正后的场 $\sigma$ 。

2. $\sigma=\nu$

此时， $\mathbf{k}_s=\mathbf{k}_\mu$ ，（7.14）中对应项对应于修正后的场 $\mu$ 。

3. 上述两个条件都不成立，最终就会发现原子响应中出现的频率和场向量数量要比初始场中多得多。这是由于相互作用的非线性的本质。

举个例子，当存在三个场入射时， $\varrho_{12}^{(3)}(\mathbf{R},\mathbf{v},t)$ 随 $e^{-i(\mathbf{k}_s\cdot\mathbf{R}-\omega_st)}$ 变化，其中

可以取以下值：

以及对应的 $\mathbf{k}_s$ 。前三个频率与所施加的电场的频率相同，但其余所有频率则对应于介质中产生的新场频率。正如这个例子所表明的那样，尽管三阶极化存在 $N^{3}$ 种贡献，但出现在三阶极化中的不同频率（ωs = ωµ - ων + ωσ）的数量却可能显著少于 $N^{3}$ 。

四波混频（Four-wave mixing）指的就是三个场在介质中产生新的场的过程。其波矢需满足相位匹配（phase matching）条件∣ks−ωs/c∣L≪1。

另一个关于（7.14）的研究点是当每个场频率发生变化时的共振位置：

7.2 N = 2：静态原子的饱和光谱学（Saturation Spectroscopy for Stationary Atoms）

考虑场景：两个外加场，且无碰撞 $\gamma=\gamma_{2}/2$

在这个场景中，由（7.9）和（7.10）可得：

前两项表示每个场的强度导致激发态占据数增加，吸收过程被“饱和”（即吸收率随光强增加而降低）。这是饱和光谱学（saturation spectroscopy）的物理基础。第二项是交叉项，表示两场干涉效应，形成空间调制的布居光栅（population grating）。其形式可化简为 $A\cos(k_{12}\cdot R+\delta_{12}t+\phi),$ 布居光栅作为介质中的非线性结构，可通过三阶极化导致两场之间的相干能量转移。

现在想要计算场中的三阶原子响应。首先假定，第一个场是一个泵浦（pump）场，其具有比第二个场——探测（probe）场，更高的强度。其思想是计算以下在探测场频率振荡的原子响应：

一阶响应由（7.8）给出。由（7.14）可以看出，当N=2时，对于三阶极化存在贡献的量有8个。均列举在表7.1中。

由于想要的在探测频率处并且对探测拉比频率是线性的三阶响应，因此存在贡献的项是 $(\mu.\nu,\sigma)=(1,1,2),(2,1,1)$ 。这些项为我们提供了由泵浦场引起的线性吸收的场强修正值，其阶数为 |χ1|²。

同时考虑方程（7.8）和（7.14）中的线性和非线性成分，可以得到：

方括号内第一项导致探测场吸收的减少，这是由于泵浦场引起的“饱和”。方括号内第二项，可能会导致探测场吸收的增加或者减少。这一“相干项或光栅项”源于泵浦场与探测场在二阶相互作用下形成的空间光栅，泵浦场通过散射与此光栅耦合，从而在三阶非线性响应中产生能量交换或新频率成分。

当 $|\delta_{1}|\gg\gamma$ 时。（7.24）可化简为：

另一方面，考虑两个场拥有相同频率但不同方向，此时，饱和项和光栅项的贡献相同，（7.24）简化为：

7.3 N=2：Saturation Spectroscopy for Moving Atoms in Counterpropagating Fields—Hole Burning

考虑场景：热蒸气玻璃管，采用方向相反的激光；一般由泵浦场和其部分反射的场（探测场）组成，探测场的吸收谱是需要观测的量。这两束光频率相同，方向相反：

7.3.1 Hole Burning and Atomic Population Gratings

在外加场的二阶近似下，由（7.9）和（7.10）可得到上态的布居：

当对上式进行空间平均时，后两项就消去了，可以得到：

第二行的近似在时成立。为了更方便理解场如何改变原子态的布居情况，引入由以下定义的在速度空间中空间平均的激发态布居密度：

在低压和环境温度下，以下情况成立：

其中u是最可能的原子速度。（7.33）被称为多普勒极限，因为多普勒宽度是线性吸收线宽的主要影响因素。在多普勒基线下，空间平均的状态2布居在时存在最大激励，因为只有那些的原子才会与场发生谐振。在图7.2中，画出了以为自变量的空间平均基态速度分布：

可以发现的是，基态的布局在处存在一个的洞。这对应于Bennett在1960年代末提出的经典的 hole-buring 模型。当一个近乎单色的场与一组具有较大（相对于自然宽度而言）不均匀分布的跃迁频率的原子集合相互作用时，就会发生烧洞现象。在固体中，通常由于介质中的应变而引入了较大的不均匀宽度；因此，固体中也会出现烧洞现象，而不仅仅是热蒸气中会出现这种情况。

（7.30）的后两项虽然在多普勒极限下被忽略，但是当时，其与时由泵浦场和探测场创建的静态光栅相关。将光栅项写作以下形式是具有建设性的：

其中：

其中 φ12 是出现在公式 (7.2) 中的场 1 和场 2 的相对相位。在这种形式下，可以看出原子布居光栅相对于公式 (7.2) 中给出的驻波场强度被偏移了一个 ξ。通过写出驻波场的两个行波分量的麦克斯韦方程，可以证明，只要 ξ≠0，这个相位偏移就可能导致两个场之间的能量交换。

7.3.2 探测场吸收率

本小节计算线性探测光场的吸收（请记住，实际上是在计算由于介质散射而导致的探测光强度的损失），并包括泵浦光场幅度二阶项对吸收的修正。首先写出：

并找出探测场拉比频率一阶量所造成的贡献。第一项表示介质对探测场的线性响应，第二项给出由于泵浦场饱和效应的修正结果。由（7.7），（7.8），（7.14），（7.27）和（7.28）可以得到：

其中在计算三阶贡献的时候采用了，因为这些导致在探测场频率的线性响应。

由（7.39）和 Maxwell-Bolch 方程可以计算探测场的吸收率。首先，取在Z轴方向。探测场振幅的稳态Maxwell-Bloch方程（6.25）如下：

其中：

由（6.18）和（7.39）可得：

并且：

其中：

（7.40）中的负号是由于探测场沿Z轴的反向传播。只关注非线性、三阶量的贡献，这是泵浦场所产生的影响。可以通过调制场1，并检测场2吸收中被调制的部分，来分离出这一项。

只保留（7.40）中的三阶贡献（7.43），可以得到：

其中

其中 $\alpha_0$ 的定义出自（4.23）。存在两个贡献，第一个是饱和项，第二个是光栅，或者说是反向散射（back-scattering）项。

7.3.2.1 饱和项

如果将被积函数写成部分分式的形式，公式 (7.46) 中的积分可以准确地用等离子体色散函数（plasma dispersion functions）来表示。在公式 (7.33) 所定义的多普勒极限下，如果将高斯函数在 vz=δ/k处进行评估，则可以得到一个近似表达式。在这种情况下，我们使用留数积分法（轮廓积分）来计算该积分，得到如下结果：

如果将该项与由公式 (7.42) 和 (7.40) 得到的线性吸收项结合起来：

由此可以得到多普勒基线下的净吸收系数：

下图展示了随吸收系数随δ变的曲线，可以看到在轮廓中心出现一个宽度为 2γ 的凹陷，这通常被称为拉姆凹陷（Lamb dip），以纪念威利斯·拉姆（Willis Lamb），他在其气体激光器理论中预测了激光功率随腔体失谐变化而出现的类似凹陷。这一凹陷在实验中具有重要意义。它可用于将激光场或谐振腔锁定到某一特定的原子频率。如果我们将激光器或腔体的频率保持在吸收曲线的中心，就可以确保该频率锁定在原子的跃迁频率上。

7.3.2.2 反向散射项

在多普勒极限下，由公式 (7.47) 给出的反向散射项 α₁₂ 为零，因为在轮廓积分中所有的极点都位于同一半平面中。光栅项也无关紧要，因为原子在其激发态寿命内会移动多个波长；因此，在对速度积分时，光栅项的贡献会被‘冲淡’掉。

另一方面，对于失谐量 |δ| ≫ ku 的情况，光栅项就不能忽略了。如果 |δ| ≫ ku，所有原子都处于远离共振的状态，此时饱和项和光栅项的相对贡献是可以相比的。

7.5 Summary

本章介绍了几个重要概念。我们已经看到，使用一个场来"泵浦"或准备原子，再用第二个场来探测这些原子是有利的。泵浦场可以修改与原子态布居相关的速度分布。在饱和光谱学中，泵浦场激发一个窄速度类别的激发态原子，这些原子随后被第二个场探测。因此，通过仅使用这些选定的原子，可以消除探测吸收光谱中的多普勒展宽。术语"饱和光谱学"有时会产生误导。我们已经看到，当用两个或更多场驱动原子系综时，还存在另一种物理过程。这些场可以创建布居光栅，任何场都可以从中散射。这种相干散射过程可以导致四波混频信号以及场之间的相干能量交换。在下一章中，我们将注意力转向三能级原子，探索在这类系统中可能出现的新型现象。